Rd Sharma Solutions Class 7 Chapter 4 Rational Numbers
Welcome to NCTB Solution. Here with this post we are going to help 7th class students for the Solutions of Rd Sharma Class 7 Mathematics, Chapter 4, Rational Numbers. Here students can easily find Exercise wise solution for chapter 4, Rational Numbers. Students will find proper solutions for Exercise 4.1, 4.2, 4.3, 4.4, 4.5 and 4.6. Our teachers solved every problem with easily understandable methods so that every students can understand easily. Here all solutions are based on the CBSE latest curriculum.
Rational Numbers Exercise 4.1 Solution
Question no – (1)
Solution :
(i) -7/5
= Numerator of -7/5 is -7
(ii) 15/-4
= Numerator of 15/-4 is 15
(iii) -17/- 21
= Numerator of -17/- 21 is -17
(iv) 8/9
= Numerator of 8/9 is 8.
(v) 5
Non zero clement.
Question no – (2)
Solution :
(i) -4/5
= Here, denominator is 5
(ii) 11/-34
= Here, denominator is – 34
(iii) -15/-82
= Here, denominator is – 82
(iv) 15
= Here, denominator is 1
(v) 0
= non zero clement
Question no – (3)
Solution :
Numerator,
= (-3) × 4
= – 12
Denominator,
= (34 – 23) × (7 – 4)
= 11 × 3
= 33
∴ Number = -12/33
Therefore, the ration number is -12/33
Question no – (4)
Solution :
In the question,
7/1, -12/1, 34/1, -73/1, 95/1
Written as integers,
= 7, -12, 34, -73, 95
Question no – (5)
Solution :
(i) -15 with denominator 1
= -15/-1
(ii) 17 with denominator 1
= -17/1
(ii) 85 with denominator 1
= 85/1
(iv) -100 with denominator 1
= -100/1
Question no – (6)
Solution :
We know, The smallest three digit number is = 100
The largest four digit number is = 9999
∴ Numerator/Denominator = 100/9999
Question no – (7)
Solution :
Positive integer,
(i) -5/-7,
(ii) 7/4,
(iii) -18/-7,
(iv) -1/-9
Negative integers,
(i) 12/-5,
(ii) 13/-9,
(iii) -95/116
Question no – (8)
Solution :
The positive rational numbers are, (ii) 9/8 and (iii) -19/-13
Question no – (9)
Solution :
The negative rational numbers are, (i) -3/7 and (iii) 9/-83
Rational Numbers Exercise 4.2 Solution
Question no – (1)
Solution :
(i) -15/-28 with positive denominator,
= 15/28
(ii) 6/-9 with positive denominator,
= -6/9
(iii) -28/-11 with positive denominator,
= 28/11
(iv) 19/-7 with positive denominator,
= -19/7
Question no – (2)
Solution :
(i) Since,
= 3/5 × 2/2
= 6/10
Question no – (3)
Solution :
(i) -14
= 5/7 × -2/-2
= -10/-14
(ii) 70
= 5/7 × 10/10
= 50/70
(ii) -28
= 5/7 × -4/-4
= -20/-28
(iv) -84
= 5/7 × -12 /-12
= -60/-84
Question no – (4)
Solution :
(i) 20
= 3/4 × 5/5
= 15/20
(ii) 36
= 3/4 × 9/9
= 27/36
(iii) 44
= 3/4 × 11/11
= 33/44
(iv) -80
= 3/4 × -20/-20
= -60/-80
Question no – (5)
Solution :
(i) -56
= 2/5 × -28/-28
= -56/-140
(ii) 154
= 2/5 × -375/-375
= -700/-1875
(iii) -750
= 2/5 × 72/72
= 154/360
(iv) 500
= 2/5 × 250/250
= 500/1250
Question no – (6)
Solution :
(i) 64
= -192/-3/108/-3
= 64/-36
(ii) -16
= -192× -1/12/ 108 ×-1/-12
= 16/9
(iii) 32
= 192× -1/6/108 × -1/4
= 32/-18
(iv) -48
= -192/ × -1/4/108 × -1/4
= -48/ 27
Question no – (8)
Solution :
(i) -14/42
= -14 × 1/7/ 42/7
= -2/6
(ii) -14/42
= 14 × -1/2/ 42 × -1/2
= 7/-21
(iii) -14/42
= 14 × -3/42 × -3
= 42/-126
(iv) -14/42
= -14 × 5/ 42 × 5
= -70/210
Question no – (9)
Solution :
The numbers that can be, written as a rational number with numerator 6 are, 1/22, 2/3, 3/4, -6/7
Question no – (10)
Solution :
The numbers that can be, written as a rational number with denominator 4 are, 7/8, 64/10, 36/- 12, 5/-4, 140/28
Question no – (11)
Solution :
(i) 3/4 and 5/12

∴ 9/12 and 5/12
= 2 × 2 × 3
= 12
(ii) 2/3, 7/6 and 11/12
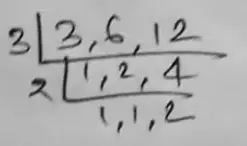
∴ 8/12, 14/12, 11/12
= 3 × 2 × 2
= 12
(iii) 8/7, 3/8, 9/14, and 20/21

∴ 120/168, 63/168, 108/108, 160/168
= 7 × 2 × 4 × 3
= 186
Rational Numbers Exercise 4.3 Solution
Question no – (1)
Solution :
(i) 65/84 = Lowest form.
(ii) -15/32 = Lowest form.
(iii) 24/128 = Mot Lowest form.
(iv) -56/- 32 = Not Lowest form.
Question no – (2)
Solution :
(i) 4/22
= 2/11
(ii) -36/180
= -1/5
(iii) 132/-428
= 33/-107
(iv) -32/-56
= 4/7
Question no – (3)
Solution :
(i) -5/7 = -25/35 = -35/49
(ii) -4/-9 = 8/18 = 12/27
(iii) 6/-13 = -12/26 = 24/52
(iv) -6/-22 = 3/11 = -15/-55
Rational Numbers Exercise 4.4 Solution
Question no – (1)
Solution :
(i) 2/10
= 1/5
∴ 2/10 in standard form is 1/5.
(ii) -8/36
= -2/9
∴ -8/36 in standard form is -2/9
(iii) 4/-16
= -1/4
∴ 4/-16 in standard form is -1/4
(iv) -15/-35
= 3/7
∴ -15/-35 in standard form is 3/7
(v) 299/-161
= 13/-7
∴ 299/-161 in standard form is 13/-7
(vi) -63/-210
= -63 ÷ 21/-210 ÷ 21
= 3/10
∴ -63/-210 in standard form is 3/10
(vii) 68/-119
= 68 ÷ 17/-119 ÷ 17
= 4/-7
∴ 68/-119 in standard form is 4/-7
(viii) -195/275
= -39/55
∴ -195/275 in standard form is -39/55
Rational Numbers Exercise 4.5 Solution
Question no – (1)
Solution :
(i) -9/12 and 8/-12
= 8/-12 = 42/-3
∴ [Equal]
(ii) -16/20 = -20/25
= 20/-25 = -4/5
∴ [Equal]
(iii) -7 /21 and 3/-9
= 3/-9 = -1/3
∴ [Equal]
(iv) -8/-14 and 13/21
= 13/21 = 13/21
∴ [Equal]
Question no – (2)
Solution :
(i) 2/3 and 5/x
= x = 15/2
So, the value of x is 15/2
(ii) -3/7 = x/4
= x = -12/7
Thus, the value of x is -12/7
(iii) 3/5 and x/- 25
= x = 3 ×(-25)/5
= -15
Therefore, the value of x is -15
(iv) 13/6 = -65/x
= x = -65/13
= -5 × 6
= -30
Hence, the value of x is -30
Question no – (3)
Solution :
(i) A number which can be expressed in the form p/q, where p and q are integers and q is not equal to zero, is called a Rational number.
(ii) If the integers p and q have no common divisor other than 1 and q is positive, then the rational number p/q is said to be in the Lowest form.
(iii) Two rational numbers are said to be equal, if they have the same Standard form form.
(iv) If m is a common divisor of a and b, then a/b = a ÷ m/b ÷ m
(v) If p and q are positive integers, then p/q is a Positive rational number and p/- q is a Negative rational number.
(vi) The standard form of -1 is -1/1
(vii) If p/q is a rational number, then q cannot be 0
(viii) Two rational numbers with different numerators are equal, if their numerators are in the same Ratio as their denominators.
Question no – (4)
Solution :
(i) Given statement is (False).
(ii) Given statement is (True).
(iii) Given statement is (False).
(iv) Given statement is (True).
(v) Given statement is (False).
(vi) Given statement is (False).
(vii) Given statement is (False).
(viii) Given statement is (False).
(ix) Given statement is (False).
(x) Given statement is (True).
Rational Numbers Exercise 4.6 Solution
Question no – (1)
Solution :
The given numbers on the number line are as follows.

Question no – (2)
Solution :
(i) -3/8, 0
= -3/8 < 0
(ii) 5/2, 0
= 5/2 > 0
(iii) -4/11, 3/11
= 3/11 > -4/11
(iv) -7/12, 5/-8
= -7/12 > 5/-8
(v) 4/-9, -3/-7
= -3/-7 > -4/9
(vi) -5/8, 3/-5
= -5/8 > -6/8
(vii) 5/9, -3/-8
= 5/9 > -3/-8
(viii) 5/-8, -7/12
= 5/8 < -7/12
Question no – (3)
Solution :
(i) -6/-13
= 6/13 < 7/13
(ii) 16/- 5, 3
= 16/-5 < 3
(iii) -4/3, 8/-7
= -3 < -12/5
(iv) -12/5, -3
= -4/3 < -8/7
Question no – (4)
Solution :
(i) -6/7 __ 7/13
= -6/7 < 7/13
(ii) -3/5 __ -5/6
= -3/5 > -5/6
(iii) -2/3 __ 5/-8
= -2/3 < -5/8
(iv) 0 __ -2/5
= 0 > -2/5
Question no – (5)
Solution :
(i) Given number,
3/5, -17/-30, 8/-15, -7/10
In ascending order,
-7/10 < -8/45 < -17/30 < 3/5
Question no – (6)
Solution :
(i) In the given question,
7/8, 64/16, 36/- 12, 5/- 4, 140/28
Now in descending order,
140/28 > 64/16 > 7/8 > – 5/4 > 36/-12
(ii) In the given question,
-3/10, 17/-30, 7/-15, -11/20
Now in descending order,
-3/10 > 7/-15 > -11/20 > 17/-30
Question no – (7)
Solution :
(i) Given statement is (False).
(ii) Given statement is (False).
(iii) Given statement is (True).
(iv) Given statement is (True).
(v) Given statement is (False).
(vi) Given statement is (True).
Next Chapter Solution :
👉 Chapter 5 👈