Warning: Undefined array key "https://nctbsolution.com/frank-icse-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Frank ICSE Mathematics Class 8 Solutions Chapter 14 Quadrilaterals and Circles
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Frank ICSE Mathematics Class 8 Math Book, Chapter 14, Quadrilaterals and Circles. Here students can easily find step by step solutions of all the problems for Quadrilaterals and Circles, Exercise 14.1, 14.2 and 14.3 Also our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 14 solutions. Here in this post all the solutions are based on latest Syllabus.
Quadrilaterals and Circles Exercise 14.1 Solution :
Question no – (1)
Solution :
Suppose the angles are 2x°, 5x°, 4x°
∴ 2x° + 5x° + 4x°/3 = 77°
or, 11x° = 3 × 77°
or, x° = (3x × 77/11)° = 21°
∴ The angles are – 2x° = 42°, 5x° = 105°, 4x° = 84°
= 360° – (42° + 105° + 84°) = 360°- 231°
= 129°
Question no – (2)
Solution :
(a) 72° + 69° + 105° + 109° = 355°
= Can’t from quadrilateral
(b) 144° + 76° + 98° + 42° = 360°
= Can from quadrilateral
(c) 108° + 87° + 66° + 99° = 360°
= Can from quadrilateral
Question no – (3)
Solution :
(b) x = (180° – 110°) = 70°
= y = 360° – (60° + 70° + 90°)
= 360° – 220°
= 140°
Question no – (4)
Solution :
(a) a + 2a = (360° – 90° – 90°) = 180°
∴ a = 180°/3 = 60°
(b) (3a + a + 20 + 80° + a + 10)° = 360°
or, (5a + 110)° = 360°
or, 5a° = 250°
∴ a = 50°
(c) (5a + 10 + 2a + 5 + 3a + 15) = 360° – 90°
or, (10a + 30)° = 270°
or, 10a° + 240°
a = 24°
Question no – (5)
Solution :
(a) (x + 60 + 75 + 105)° = 360°
or, (x + 240)° = 360°
or, x = 360° – 240°
= 120°
Since a, b, c, d are external angles a + b +c + d = 360°
(b) (x + 110 + 95 + 70)° = 360°
or, (x + 275°) = 360°
or, = 360° – 275° = 85°
Question no – (6)
Solution :
∠ABC = 360° – (100° + 70° + 60°) = 360° – 230° = 130°
∠DOC = 180° – (∠ODC + ∠OCD)
= 180° – (70°/2 + 60°/2) = 180° – (35° + 30°)
= 180° – 65°
= 115°
Quadrilaterals and Circles Exercise 14.2 Solution :
Question no – (8)
Solution :
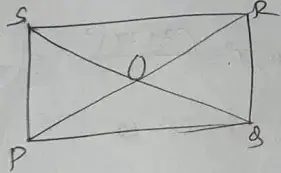
Clearly PO = OQ
or, 5x – 6 = 3x + 4
or, 5x – 3x = 4 + 6
or, 2x = 10
or, x = 10/5 = 2
Question no – (9)
Solution :
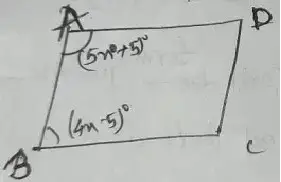
= (5x + 5)° + (4x – 5)° = 180°
or, (5x + 4x)° = 180 =°
or, 9x = 180°
or, 180°/9 = 20°
The angles – A = 5x° + 5° = 105°
B = (4x – 5)° = 75°
C = A = 105°
D = B = 75°
Question no – (10)
Solution :
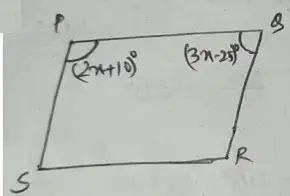
∴ (2x + 10)° + (3x – 25°) = 180°
or, 5x – 15 = 180°
or, 5x = 195°
or, x = 39°
∴ P = (2x + 10°) = (78 + 10)° = 88°
Q = (3x – 25)° = 117° – 25° = 92°
R = P = 88°
S = Q = 92°
Question no – (11)
Solution :
Suppose the angles are – 2x°, 3x°, 5x°, 8x°
= (2x + 3x + 5x + 8x)° = 360°
or, x = 20°
Angles = 40°, 60°, 100°, 160°
Question no – (12)
Solution :
Suppose the angles are – 3x°, 4x°, 5x°, 6x°
∴ (3x + 4x + 5x + 6x)° = 360°
or, 18x = 360°
or, x = 20°
∴ Angles = 60°, 80°, 100°, 120°
Question no – (13)
Solution :
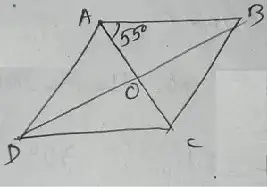
Since ∠OAB = 55°,
then, ∠BAD = 110°
∠ADC = 180° – 110° = 70°
∠BAD = BCD = 110°
∠ADC = ∠ABC= 70°
Question no – (14)
Solution :
(a) Y = 105°,
X = (180° – 105°)
= 75°
= x
(b) x = 180° – 40° = 140°
y = z = 360° – 80°/2
= 280°/2
= 140°
(c) 4x – 3 = 3x + 2
or [x = 5]
= (y + 10)° = 35°
or, y = 25°
= 35° + z + 70° = 180°
or, x = 180° – (35° + 70°) = 75°
(d) x + 30° + 110° = 180°
or, x = 40° = z
= y = 110°
(e) x = 90°
= z = y = 180° – (90° + 60°)
= 30°
(f) z = 180° – 70° = 110°
= y = 180° – 100° = 80°
Again, x + y = z
∴ x = 110° – 80° = 30°
or, x = 80° = 110°
Question no – (15)
Solution :
(a) x + 5 = 20
or, x = 20 – 5 = 15
= y + 15 = 25
or, y = 25 – 15 = 10
(b) 5x = 15
or, x = 15/5 = 3
= 3y + 1 = 25
or, 3y = 24
or, y = 24/3 = 8
Question number – (16)
Solution :
= ∠SPO = ∠SPQ + ∠QPO = 90° + 60° = 150°
∴ ∠x = ∠y = 1/2 (180° – 150°)
= 1/2 (30°)
= 15°
Question no – (17)
Solution :
∠x = ∠DAB – ∠OAB = 90° – 60° = 30°
∠y = 1/2 [180° – 30°]
= 1/2 [150°]
= 75°
Question no – (18)
Solution :
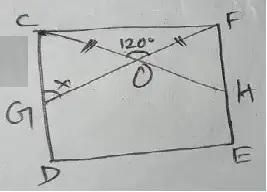
Since, △COF is isosceles therefore ∠OCF = ∠OFC
∠OFC = 1/2 (180° – 120°) = 30°
∠x = 180° – (30° +90°)
= 180° – 120°
= 60°
Question no – (19)
Solution :
Clearly BD = AC
∴ 5a – 3 = a + 5
or, 4a = 8
= a = 8/4 = 2
Now, clearly y = x = 47°
and = {180° – 2 (90° – 47°)}
= {(180° – 86°} = 94°
Question no – (20)
Solution :
∠x = 1/2 (180° – 112°) = 1/2 × 68° = 34°
∠y = 90° – ∠x
= 90° – 34° = 56°
∠z = ∠y = 56°
Question no – (21)
Solution :
= x + 150° = 180°
or, x = 180° – 150° = 30°
Now, x = y = 30°
and z = 180° – (x + y)
= 180° – 60°
= 120°
Question no – (22)
Solution :
∠WXY= ∠WZY = 360° + 44° = 80°
Now, ∠a = 180° – {180° – 110°) + 44°} = 60°
Question no – (23)
Solution :
Clearly P = Q = 8x + 20°
= 10x – 10°
or, 10x – 8x
= 20° + 10°
or, 2x = 30°
or, x = 15°
∠Q = 180° – ∠P
= 180° – {8 × 15°) + 20°}
= 180° – 140° = 40°
Question no – (24)
Solution :
Since CF = DE then ∠FCD = ∠EDC
and, ∠CFE = ∠DEF
∴ ∠a = ∠b = 1/2 [360° – (2 × 108°)] = 72°
Question number – (25)
Solution :
= x = 180° – (90° + 30°) = 60°
= z = 58°, y = 180° – (90° + 58°) = 32°
Question no – (26)
Solution :
= x = 32°, y = 32°
= z = 180° – {32° + 32°} = 116°
Question no – (27)
Solution :
∠a = 180° – 50° = 130°
∠b = 180° – (180° – 154°) = 154°
Question no – (28)
Solution :
∠ABC = 180° – 45° = 135°
∴ ∠x = 135° – 35° = 105°
Next Chapter Solution :
👉 Chapter 18 👈
Chapter 15