Samacheer Kalvi Class 8 Maths Chapter 5 Geometry Solutions
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students by providing Solutions for Samacheer Kalvi Class 8 Maths chapter 5 Geometry. Here students can easily find all the solutions for Geometry Exercise 5.1, 5.2, 5.3, 5.4 and 5.5. Also here our Expert Maths Teacher’s solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 5 solutions. Here all the solutions are based on Tamil Nadu State Board latest syllabus.

Geometry Exercise 5.1 Solutions :
(1) Fill in the blanks with the correct term from the given list :
(in proportion, similar, corresponding, congruent, shape, area, equal)
(i) Corresponding sides of similar triangles are ___
Solution :
Corresponding sides of similar triangles are Proportion
(ii) Similar triangles have the same ___ but not necessarily the same size.
Solution :
Similar triangles have the same “Shape” but not necessarily the same size.
(iii) In any triangle __ sides are opposite to equal angles.
Solution :
In any triangle Equal sides are opposite to equal angles.
(iv) The symbol ≡ is used to represent __ triangles.
Solution :
The symbol ≡ is used to represent Congruent triangles.
(v) The symbol ∼ is used to represent __ triangles.
Solution :
The symbol ∼ is used to represent Similar triangles.
Question no – (2)
In the given figure, ∠CIP ≡ ∠COP and ∠HIP ≡ ∠HOP. Prove that IP ≡ OP
Solution :
Given, ∠CIP ≡ ∠COP
∠HIP ≡ ∠HOP
∴ HP is the common
∴ HI = HO and ∠I= ∠O
∴ △ HIP ≡ △HOP
∴ IP ≡ OP [Proved] [by SAS]
Question no – (3)
In the given figure, AC ≡ AD and ∠CBD ≡ ∠DEC. Prove that △BCF ≡ △EDF
Solution :
Given, AC ≡ AD
∠CBD ≡ ∠DEC
∠BFC ≡ ∠EFD [vertically opposite angle ]
and CD is common and BC ≡ ED [If angle then sides]
∴ △BCF ≡ △EDF
Question no – (4)
In the given figure, △BCD is isosceles with base BD and ∠BAE ≡ ∠DEA . Prove that AB ≡ ED
Solution :
△BCD is isosceles with base BD and ∠BAE ≡ ∠DEA
△BCD = 1/2 △ACE and BD is common and AC ≡ EC [If angle then sides]
∴ AB ≡ ED [Proved]
Question no – (5)
In the given figure, D is the midpoint of OE and ∠CDE = 90°. Prove that △ODC ≡ △EDC
Solution :
D is the midpoint of OE
∴ OD ≡ DE [D is mid point]
∠CDE = 90° = ∠CDO [D is mid point]
CD ≡ CD [reflexive property]
∴ △ODC ≡ △EDC [SAS property] [Proved]
Question no – (9)
In the given figure, if △EAT ∼ △BUN, find the measure of all angles
Solution :
∠E = ∠B = x°
∠A = ∠U = 2x°
∠T = ∠N = (x+40)°
∴ x + 2x + x + 40° = 180°
= 4x = 180 – 40
= x = 140/4 = 35
∴ ∠E = ∠B = 35°
∠A = ∠U = 2 × 35 = 70°
∠T = ∠N = (35+40) = 75°
Question no – (9)
In the given figure, UB ||AT and CU ≡ CB Prove that △CUB ∼ △CAT and hence △CAT is isosceles
Solution :
Given, UB ||AT
CU ≡ CB
∠ACT ≡ ∠UCB [common]
CU/CA = CB/CT [The sides are proportional]
∴ △CUB ∼ △CAT [by SAS]
Objective Type Question Solutions :
Question no – (11)
Two similar triangles will always have ___ angles
(A) acute
(B) obtuse
(C) right
(D) matching
Solution :
Correct option – (C)
Two similar triangles will always have right angles.
Question no – (12)
If in triangles PQR and XYZ, PQ/XY= QR/YZ then they will be similar if
(A) ∠Q = ∠Y
(B) ∠P = ∠Y
(C) ∠Q = ∠X
(D) ∠P = ∠Z
Solution :
Correct option – (A)
If in triangles PQR and XYZ, PQ/XY= QR/YZ then they will be similar if ∠Q = ∠Y
Question no – (14)
If △ABC ∼ △PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Solution :
Given, ∠A = 53° , ∠Q = 77°
∴ ∠A + ∠Q + ∠R = 180°
= 53°+77°+∠R = 180°
= ∠R = 180° – 53° – 77°
= ∠R = 50°
Hence, the correct option is (A)
Question no – (15)
In the figure, which of the following statements is true
(A) AB = BD
(B) BD < CD
(C) AC = CD
(D) BC = CD
Solution :
Option (C) AC = CD – This statement is True.
Geometry Exercise 5.2 Solutions :
(1) Fill in the blanks :
(i) If in a ∆PQR, PR2 = PQ2, then the right angle of ∆PQR is at the vertex __
Solution :
If in a ∆PQR, PR² = PQ² + QR², then the right angle of ∆PQR is at the vertex QR.
(ii) If l and ‘m’ are the legs and n is the hypotenuse of a right angled triangle then, l2 = __
Solution :
If ‘l’ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l² = n² – m².
(iii) If the sides of a triangle are in the ratio 5 : 12 : 13 then, it is __
Solution :
If the sides of a triangle are in the ratio 5 : 12 : 13 then, it is “Right angled triangle”.
(iv) The medians of a triangle cross each other at __
Solution :
The medians of a triangle cross each other at “Centroid”.
(v) The centroid of a triangle divides each medians in the ratio __
Solution :
The centroid of a triangle divides each medians in the ratio 2 : 1
(2) Say True or False :
(i) 8, 15, 17 is a Pythagorean triplet.
Solution :
Statement is True
= 8² + 15²
= 64 + 225
= 289 = 17²
(ii) In a right angled triangle, the hypotenuse is the greatest side.
Solution :
Statement is True
(iii) In any triangle the centroid and the incentre are located inside the triangle.
Solution :
Statement is True
(iv) The centroid, orthocentre, and incentre of a triangle are collinear.
Solution :
Statement is True
(v) The incentre is equidistant from all the vertices of a triangle.
Solution :
Statement is False.
Question no – (3)
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
(i) 8, 15, 17
(ii) 12, 13, 15
(iii) 30, 40, 50
(iv) 9, 40, 41
(v) 24, 45, 51
Solution :
(i) 8, 15, 17
= 8² + 15²
= 64 + 225 +
= 289 = 17² satisfied.
(ii) 12, 13, 15
= 12 + 13²
= 144 + 169
= 223 = 15² Not satisfied.
(iii) 30, 40, 50
= 30² + 40²
= 900 + 1600
= 2500 = (50)² satisfied.
(iv) 9, 40, 41
= 9² + 40²
= 81 + 1600
= 1681 = (41)² satisfied.
(v) 24, 45, 51
= (24)² + (45)²
= 576 + 2025
= 2601 = (51)² satisfied.
Question no – (3)
Find the unknown side in the following triangles.
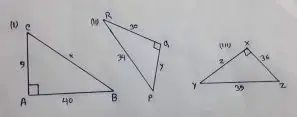
Solution :
Figure – (i)
By Pythagoras theorem
x² = 9²+40²
= 81+ 1600
= x² = 1681
= x = 41
Figure – (ii)
By Pythagoras theorem
y² = (34)²-(30)²
= 1156-900
= 256
= y² = (16)²
= y = 16
Figure – (iii)
By Pythagoras theorem
z² = (39)² – (36)²
= 1521 – 1296
= 225
= z² = (15)²
= z = 15
Question no – (5)
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height.
Solution :
AB = AC = 13 cm
BC = 24 cm
D is the midpoint
∴BD = CD = BC/2 = 24/2 = 12 cm
∴ By Pythagoras theorem
(AD)²+(CD)² = (AC)²
∴ (AD)² = (AC)²-(DC)²
= (13)² – (12)² = 169 – 144 = 25
∴ (AD)² = 25 = (5)²
∴ Height (AD) = 5
Question no – (6)
Find the distance between the helicopter and the ship.
Solution :
AP = 80 m , PS = 150 m
∴ (AS)² = (AP)² + (PS)²
= d² = (80)² + (150)²
= d² = 6400 + 22500
= d = √28900
= √170 × 170
= 170
∴ The distance between the helicopter and the ship is 170 cm.
Question no – (7)
In triangle ABC, line l1 is a perpendicular bisector of BC. if BC = 12 cm, SM = 8 cm, find CS
Solution :
BC = 12 cm, SM = 8 cm
∴ BM = MC = BC/2 = 12/2 = 6 cm
∴ By Pythagoras theorem
(CS)² = (SM) ² + (MC)²
= x² = 8² + 6²
= x² = 64 + 36
= x² = 100
= x = 10
∴ CS = 10 cm.
Question no – (8)
Identify the centroid of ∆PQR.
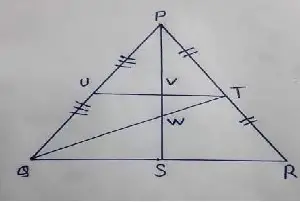
Solution :
Here, QW : WT = 2 : 1
PW : WS = 2 : 1
and if we join UR it is also in the ratio RW : WU = 2 : 1
∴ The centroid of the ∆PQR is W
Question no – (10)
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. if the length of GA is 3 cm, find XA
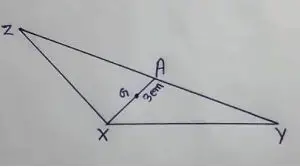
Solution :
XG : GA = 2K : K
Here, K = 3 cm
∴ XG = 2 × 3 = 6 cm
and GA = 3 cm
∴ XA = XG + GA
= 6 + 3
∴ XA = 9 cm
Question no – (11)
If I is the incentre of ∆XYZ, ∠IYZ = 30° and ∠IZY = 40°, find ∠YXZ
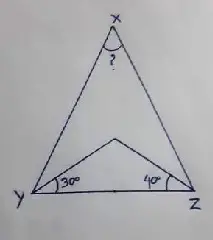
Solution :
I is the incentre
∠IYZ = 30° and ∠IZY = 40°
∴ ∠XZY = 2×∠IZY = 2×40° = 80°
∠XYZ = 2×∠IYZ = 2×30° = 60°
Now, ∠XYZ + ∠XZY + ∠YXZ = 180°
= 60° + 80° + ∠YXZ = 180°
= ∠YXZ = 180° – 140°
= ∠YXZ = 40°
Objective Type Question Solutions :
Question no – (12)
If ∆GUT is isosceles and right angled, then ∠TUG is
(A) 30°
(B) 40°
(C) 45°
(D) 55°
Solution :
Correct option – (C)
If ∆GUT is isosceles and right angled, then ∠TUG is 45°
Question no – (13)
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is
(A) 28 cm
(B) 20 cm
(C) 24 cm
(D) 21 cm
Solution :
(12)² + (16)²
= 144 + 256
= 400
= (20)²
Hence, correct option is – (B)
Question no – (14)
The area of a rectangle of length 21 cm and diagonal 29 cm is
(A) 609 cm²
(B) 580 cm²
(C) 420 cm²
(D) 210 cm²
Solution :
(AB)² = (29)² – (21)²
= 841 – 441
= 400
∴ (AB)² = (20)²
AB = (20)
∴ Area of rectangle is = AB × BC
= 20 × 21
= 420 cm
Thus, correct option – (C)
Question no – (15)
The sides of a right angled triangle are in the ratio 5:12:13 and its perimeter is 120 units then, the sides are __
(A) 25, 36, 59
(B) 10, 24, 26
(C) 36, 39, 45
(D) 20, 48, 52
Solution :
Correct option – (D)
= 20, 48, 52
= 20 + 48 + 52
= 120 units
Geometry Exercise 5.3 Solutions :
Question no – (2)
From the figure, prove that ∆SUN ∼ ∆RAY
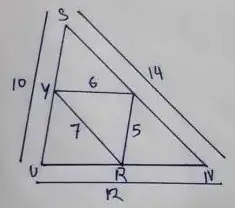
Solution :
SU/AR = SN/YR = UN/YA = 1/2
∆SUN ∼ ∆RAY [By SSS property]
[Proved]
Question no – (3)
The height of a tower is measured by a mirror on the ground at R by which the top of the tower’s reflection is seen. find the height of the tower. if ∆PQR ∼ ∆STR
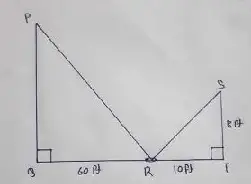
Solution :
(SR)² = (Rt)² + (ST)²
= 10² + 8²
= SR = √100 + 64
= √164
∆PQR ∼ ∆STR
∴ PQ/ST = PR/SR = QR/RT
= PQ/8 = PR/√164 = 60/10
∴ PQ/8 = 60/10
PQ = 48
∴ The height of the tower IS 48 ft.
Question no – (4)
Find the length of the support cable required to support the tower with the floor.
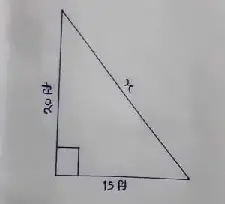
Solution :
(AC)² = (AB)² + (BC)²
= x² = (20)² + (15)²
x = √400 + 225
= √625
= 25 ft.
Hence, the length of the support cable required is 25 ft.
Question no – (5)
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason.
Solution :
The screen wide
= (25×7) inches
= 175 inches.
She need 175 inch cabinet and she has 20 inches wide cabinet. So the TV not fit into the cabinet.
Challenging Problem Solutions :
Question no – (6)
In the figure, ∠TMA ≡ ∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. prove that ∆PIN ∼ ∆ATM
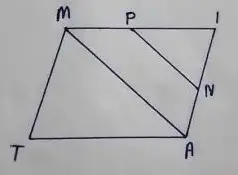
Solution :
P and N are midpoint of MI and AI respectively
∴ IP/MP = IN/AI = 1/2
and ∠MIA ≡ ∠PIN [∠I is common]
∴ ∆PIN ∼ ∆ATM [by SAS property]
[Proved]
Question no – (8)
The diagonals of the rhombus is 12 cm and 16 cm. Find its perimeter.
Solution :
In ∆DOC,
= (DC)² = 8² + 6²
= DC = √64 + 36
= √100
= 10
∴ Perimeter of the Rhombus – 4a
= 4 × 10
= 40 cm
Therefore, the Its perimeter is 40 cm.
Question no – (9)
In the figure, find AR
Solution :
(FR)² = (RI)² – (FI)²
FR = √(17)² – (15)²
= √289 – 225
= √64
= 8
(AF)² = (AI)² – (FI)²
AF = √(25)² – (15)²
= √625 – 225
= √400
= 20 ft
∴ AR = AF + FR = (20 + 8) = 28 ft.
Question no – (10)
In ∆DEF, DN, EO, FM are medians and point P is the centroid. find the following
(i) IF DE = 44, then DM = ?
(ii) IF PD = 12, then PN = ?
(iii) If DO = 8, then FD = ?
(iv) IF OE = 36 then EP = ?
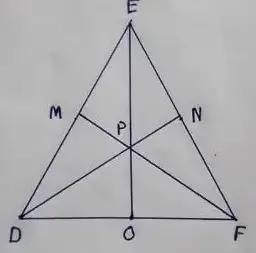
Solution :
NP/PN = FP/PM
= EP/OP
= 2/1
(i) IF DE = 44, then DM
= 44/2
= 22
(ii) IF PD = 12, then PN
= 12/2
= 6
(iii) If DO = 8, then FD
= 2 × DO
= 2 × 8
= 16
(iv) IF OE = 36 then EP
= 36 × 2/3
= 24
Geometry Exercise 5.4 Solutions :
(I) Construct the following quadrilaterals with the given measurements and also find their area.
(1) ABCD, AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.
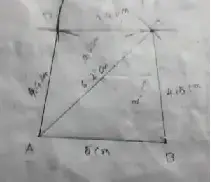
Solution :
AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC= 6.2 cm
Area of the quadrilateral ABCD
= 1/2 × d × (h_1+h_2)
= 1/2 × 6.2 × (2.6+3.6)
= 1/2 × 6.2 × 6.2
= 19.22 cm²
∴ Area = 19.22 cm²
(2) PLAY, PL = 7 cm, LA = 6 cm, AY = 6 cm, PA = 8 cm and LY = 7 cm.
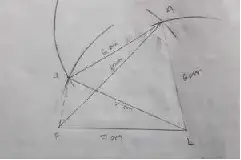
Solution :
Area of the quadrilateral Play,
= 1/2 × d × (h_1+h_2)
= 1/2 × 7 × 8 cm²
= 24 cm²
(3) PQRS, PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q = 120°
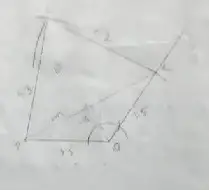
Solution :
Area of the quadrilateral PQRS
= 1/2 × d × (h_1+h_2)
= 1/2 × 6 × (4.1 +3.6)
= 3 × 7.6
= 22.8 cm²
(4) MIND, MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°
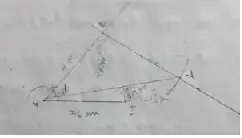
Solution :
Area of the quadrilateral MIND
= 1/2 × d × (h_1 + h_2)
= 1/2 × 6 × (2.5+0.7)
= 3 × 3.2
= 9.6 cm²
(5) AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.
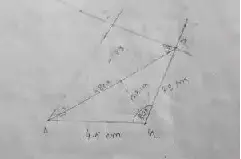
Solution :
Area of the quadrilateral AGRE
= 1/2 × d × (h_1 + h_2)
= 1/2 × 6.8 × (2.3 + 2.5)
= 3.4 × 4.8
= 16.32
(II) Construct the following trapeziums with the given measures and also find their area.
(1) AIMS with AI || SM, AI = 6 cm, IM = 5 cm, AM = 9 cm and MS = 6.5 cm
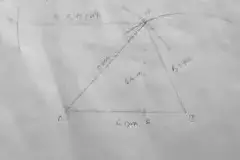
Solution :
Area of the trapezium AIMS
= 1/2 × h × (a + b)
= 1/2 × 4.5 × (6 + 6.5) cm²
= 1/2 × 4.5 × 12.5 cm²
= 28.125 cm²
∴ Area is 28.125 cm².
(2) CUTE with CU || ET, CU = 7 cm, ∠UCE = 80° CE = 6 cm and TE = 5 cm
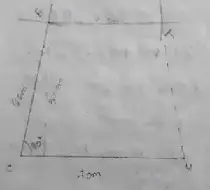
Solution :
Area of the trapezium CUTE
= 1/2 × h × (a+b)
= 1/2 × 5.9 × (7+5)
= 1/2 × 5.9 × 12
= 35.4 cm²
∴ Area is 35.4 cm²
(3) ARMY with AR || YM, AR = 7 cm, RM = 6.5 cm ∠RAY = 100° and ∠ARM = 60°
Solution :
Area of the trapezium ARMY
= 1/2 × 5.6 × (4.7+7)
= 2.8 × 11.7
= 32.76 cm²
(4) CITY with CI || YT, CI = 7 cm, IT = 5.5 cm, TY = 4 cm and YC = 6 cm
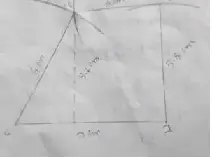
Solution :
Area of the trapezium CITY
= 1/2 × 58.2 × (7+4)
= 2.6 × 11
= 28.6 cm²
∴ Area is 28.6 cm².
Geometry Exercise 5.5 Solutions :
(I) Construct the following parallelograms with the given measurements and find their area.
(1) ARTS, AR = 6 cm, RT = 5 cm and ∠ART = 70°
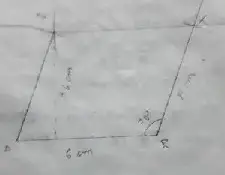
Solution :
Area of the parallelograms
= bh sq.cm
= 6 × 4.6 sq.cm
= 27.6 sq.cm
So, area is 27.6 sq.cm
(2) CAMP, CA = 6 cm, AP = 8 cm and CP = 5.5 cm
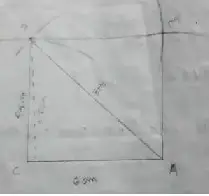
Solution :
Area of the parallelograms
= 6 × 5.5 cm²
= 33 cm²
EARN, ER = 10 cm, AN = 7 cm and ∠EOA = 110° where ER and AN intersect at O

Solution :
Area of the parallelogram
= 7 × 4.6 cm²
= 32.2 cm²
So, area is 32.2 cm²
(4) GAIN, GA = 7.5 cm, GI = 9 cm and ∠GAI = 100°

Solution :
Area of the parallelogram
= 7.5 × 3.5 cm²
= 25.5 cm²
∴ Area is 25.5 cm²
(II) Construct the following rhombuses with the given measurements and also find their area.
(i) FACE, FA = 6 cm and FC = 8 cm
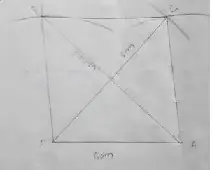
Solution :
Area of the Rhombus FACE.
= 1/2 × d_1 × d_2
= 1/2 × 8 × 8.9 cm²
= 35.6 cm²
∴ Area is 35.6 cm²
(ii) CAKE, CA = 5 cm and ∠A = 65°
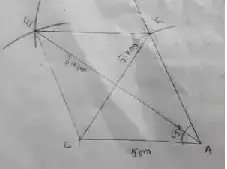
Solution :
Area of Rhombus CAKE
= 1/2 × 5.4 × 8.4 cm²
= 22.68 cm²
Therefore, the area is 22.68 cm².
(iii) LUCK, LC = 7.8 cm and UK = 6 cm

Solution :
Area of the Rhombus LUCK is
= 1/2 × 7.8 × 6 cm²
= 23.4 cm²
(iv) PARK, PR = 9 cm and ∠P = 70°
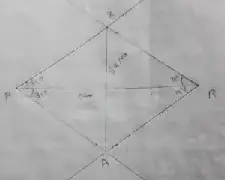
Solution :
Area of the Rhombus is,
= 1/2 × 9 × 6.3 cm²
= 28.35 cm²
∴ The area is 28.35 cm²
(III) Construct the following rectangles with the given measurements and also find their area.
(i) HAND, HA = 7 cm and AN = 4 cm
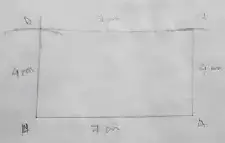
Solution :
Area of the rectangle
= 7 × 4
= 28 cm²
So, the area is 28 cm
(ii) LAND, LA = 8 cm and AD = 10 cm
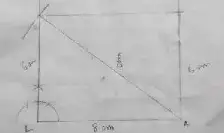
Solution :
Area of the rectangle
= 7 × 4
= 28 cm²
So, the area is 28 cm
(IV) Construct the following squares with the given measurements and also find their area.
(i) EAST, EA = 6.5 cm
Solution :
Area of the square
= a² cm²
= 6.5 × 6.5 cm²
= 42.25 cm²
(ii) WEST, WS = 7.5 cm

Solution :
Area of the square
= (5.4)² cm²
= 29.16 cm²
Therefore, the area of the square will be 29.16 cm²
Next Chapter Solution :
👉 Statistics