Rd Sharma Solutions Class 7 Chapter 14 Lines and Angles
Welcome to NCTB Solution. Here with this post we are going to help 7th class students for the Solutions of Rd Sharma Class 7 Mathematics, Chapter 14, Lines and Angles. Here students can easily find Exercise wise solution for chapter 14, Lines and Angles. Students will find proper solutions for Exercise 14.1 and 14.2. Our teachers solved every problem with easily understandable methods so that every students can understand easily. Here all solutions are based on the CBSE latest curriculum.
Lines and Angles Exercise 14.1 Solution
Question no – (1)
Solution :
Each pair of adjacent angles of the figure are ∠AOB, ∠BOD, ∠AOB, ∠AOC, ∠COD, ∠BOC, ∠COD.
Question no – (2)
Solution :
Adjacent angles for Figure – (i)
∠BAC, ∠DAC; ∠ACB ∠FCB; ∠ABC ∠ABF
Adjacent angles for Figure – (ii)
∠ADC, ∠ADB; ∠BAD, ∠DAC.
Question no – (3)
Solution :
(i) Each linear pair in the figure are,
∠1, ∠2; ∠2, ∠4 ; ∠3, ∠4 ; ∠3, ∠4 ;
∠1 ∠3, ∠6, ∠5, ∠5, ∠7; ∠7, ∠8; ∠6, ∠8
(ii) Each pair of vertically opposite angles in the figure are,
∠1, ∠4; ∠2, ∠3; ∠5 ∠8; ∠6, ∠7
Question no – (4)
Solution :
No, they are adjacent angles in the given figure.
Question no – (5)
Solution :
(i) Given angle is 35°
= (90 – 35)
= 55°
(ii) Given angle is 72°
= (90 – 72)
= 18°
(iii) Given angle is 45°
= (90 – 72)
= 45°
(iv) Given angle is 85°
= (90 – 85)
= 5°
Question no – (6)
Solution :
(i) Supplement of 70°
= (180 – 70)
= 110°
(ii) Supplement of 120°
= (180 – 120)
= 60°
(iii) Supplement of 135°
= (180 – 135)
= 45°
(iv) Supplement of 90°
= (180 – 90)
= 90°
Question no – (7)
Solution :
(i) Given, 25°, 65°
= (25 + 65)
So, its complementary
(ii) Given, 120°, 60°
= (120 + 60) = 180
So, its complementary
(iii) Given, 63°, 27°
= 63 + 27 = 90
So, its complementary
(iv) Given, 100°, 80°
= 100 + 80
= 180
So, its complementary.
Question no – (8)
Solution :
(a) Obtuse :
= Two angles can not be supplementary, if both of them are Obtuse.
(b) Right :
= Two angles is supplementary, if both of them are Right.
(c) Acute :
= Two angles can not be supplementary, if both of them are Acute.
Question no – (9)
Solution :
The four pairs of supplementary angles are in the given figure are,
(i) ∠COA, ∠AOD
(ii) ∠AOD, ∠BOD
(iii) ∠BOD, ∠COB
(iv) ∠BOC, ∠AOC
Question no – (10)
Solution :
(i) Name two linear pairs
= ∠ABE, ∠EBC, and ∠ABD, ∠DBC.
(ii) Name two pairs of supplementary angles?
= ∠ABE, ∠EBC and ∠ABD, ∠CBD
Question no – (11)
Solution :
Measure of each angle,
= x + x = 180
= x = 180/2
= x = 90°
Therefore, the measure of each angle 90°.
Question no – (12)
Solution :
Given, Complement of an angle is 28°
∴ Supplement angle,
= 180 – 28
= 152°
Therefore, the supplement of the angle is 152°
Question no – (13)
Solution :
Linear :
∠1, ∠2, ∠2, ∠3, ∠3, ∠4, ∠4, ∠1, ∠1, ∠5, ∠5, 6, ∠6, ∠7, ∠7, ∠8, ∠8, ∠5, ∠9, ∠10 ∠11, ∠10, ∠11, ∠12, ∠12, ∠9
Opposite angle :
∠1, ∠3, ∠2, ∠4, ∠5, ∠7, ∠6, ∠8, ∠9, ∠11, ∠10, ∠12
Question no – (14)
Solution :
According to the given question,
∠1 = 70
∴ ∠3 = 2 × 70 = 140°
∠2 = ∠4
∠DOA + ∠COB + ∠DOB + ∠AOC = 360°
= 2∠COB = 360 – 140 – 140
= ∠COB = 80/2
= 40°
Hence, the magnitudes of ∠2 = 40° , ∠3= 140° , and ∠4 = 40°
Question no – (15)
Solution :
We can you say about its other angle,
That the other angle has = 90°
Question no – (16)
Solution :
Then the other angle is Acute angle.
Question no – (17)
Solution :
The other angle is an Obtuse angle.
Question no – (18)
Solution :
No, two acute angles cannot form a linear pair.
Question no – (19)
Solution :
Complement of 65° does not exist.
Question no – (20)
Solution :
Figure – (i)
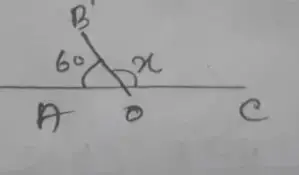
= x = 180° – 60°
∴ x = 120
Figure – (ii)
= So, 3x + 2x = 180°
= x = 180/5
∴ x = 36
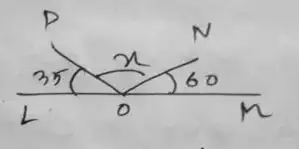
Figure – (iii)

= x + 35 + 60 = 180°
= x = 180 – 60 – 35
∴ x = 85
Figure – (iv)
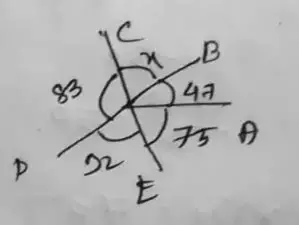
= 83 + x + 47 + 75 + 92 = 36°
= x = 360 – 297
∴ x = 63
Figure – (v)
= x + 2x + 2x + 3x = 360
= 8x = 36°
= x =36°/8
∴ x = 45°
Figure – (vi)
= 3x = 105
∴ x = 35°
Question no – (21)
Solution :
∠1 = ∠3 = 65°
And ∠1 + ∠3 + ∠2 + ∠4 = 36°
= 65 + 65° + ∠2 + ∠2 = 36°
= 2 (∠2) = 36° – 130
= ∠2 = 230/2
= 115°
∴ ∠1 = ∠3 = 65°
∠2 = ∠4 = 115°
Therefore, all the angle are ∠2 = 115°, ∠3 = 65°, ∠4 = 115°
Question no – (22)
Solution :
(i) If x = 25°, what is the value of y?
= 2y + 5 + 3x = 180°
= 2y + 5 + 75 = 180°
= 2y = 180 – 80
∴ y = 50°
(ii) If y = 35°, what is the value of x?
= 2y + 5 + 3x = 180°
= 2 × 35 + 5 + 3x = 180
= 3x = 180 – 75
= x = 105/3
∴ x = 35°
Question no – (23)
Solution :
Adjacent angles are :
= ∠AOD, ∠COD ∠BOC, ∠DOC
∠AOB, ∠DOB, ∠AOC ∠COB
Linear pairs are :
∠AOD, ∠BOD and ∠AOC, ∠BOC
Question no – (24)
Solution :
From the question,
x + x + 10 + x +20 = 180°
= 3x = 180 – 30
= x = 150/3
∴ x = 50
∴ ∠BOC = x + 20 = 70
∴ ∠COD = x = 50
∴ ∠AOD = x + 10 = 60
Question no – (25)
Solution :
When two lines intersect in a point, Then four angles are formed.
Question no – (27)
Solution :
We can find the value of x as follows :
= 3x + 3x = 180
= x = 180/6 = 30
∴ x = 30
Therefore, the value of x is 30.
Question no – (28)
Solution :
We can find the x as follows :
= 70 + 2x = 180
= 2x = 180 – 70
= x = 110/2
∴ x = 55
Hence, the x is = 55°
Question no – (29)
Solution :
= 60 + 4x + 40 = 180
= 4x =180 – 100
= x = 80/4
∴ x = 20°
Thus, the x = 20°
Question no – (31)
Solution :
As per the question,
∠x = ∠u
= x + 90 + 50 = 180
= x = 180 – 14°
∴ x = 4°
∴ ∠u = 40
∴ ∠z = 90°
∴ ∠y = 50°
Therefore, the values of x = 4, u = 40, z = 90, y = 50.
Question no – (32)
Solution :
According to the given Question,
∠y = 25°
∴ ∠x = ∠z
Here, ∠x + ∠y + ∠z + 25 = 36°
= 25 + ∠y + ∠y + 25 = 36°
= 2 ∠y = 36 – 50
= y = 310/2
= 155
∴ ∠x = 155°
= ∠y = 25°
=∠z = 155°
Therefore, the value of x will be 155°, y will be 25° and z will be 155°.
Lines and Angles Exercise 14.2 Solution
Question no – (1)
Solution :
(i) Alternate and corresponding angles in Fig. 58. (i).
Alternative angles are,
∠BGH and ∠CHG and ∠AGH and ∠DHG.
(ii) Angles alternate to ∠d and ∠g and angles corresponding to angles ∠f and ∠h in Fig. 58 (ii).
Corresponding angles are,
∠EGB and ∠GHD
∠BGH and ∠DHF
∠EGA and ∠GHC
∠AGH and ∠CHF
(iii) Angle alternate to ∠PQR, angle corresponding to ∠RQF and angle alternate to ∠PQE in Fig. 58 (iii).
Angle corresponding to ∠RQF = ∠BRA
Angle alternative to ∠PQE = BRA
Question no – (2)
Solution :
All other angles in the figure are,
∠QMD = 120°, ∠MLB = 120°
∠ALM = 60°, ∠DML = 60°
∠PLB = 60°, ∠CML = 120°
Question no – (3)
Solution :
Since, ∠LMD = ∠ALM
∴ ∠ALM = 35°
And ∠PLA = 180° – 35 = 145°
Question no – (4)
Solution :
Alternative to ∠13 = ∠7
Corresponding to ∠15 = ∠7
alternative to ∠15 = ∠5
Question no – (5)
Solution :
Let, ∠1 = 4°
= ∠1 + ∠2 = 180°
= ∠2 = 140 = ∠4
and ∠2 = ∠6 = 140°
∠6 + ∠5 = 180°
= ∠5 = 180 – 140 = 40
∠5 = ∠3 = 40°
∠3 = ∠7 = 40
∠4 = ∠8 = 140°
Question no – (6)
Solution :
Given in the question,
∠1 = 75
∠1 + ∠2 = 180°
∠2 = 180 – 75 = 105°
∠2 = ∠6 = 105°
And ∠5 pair
∠6 + ∠5 = 180
= ∠5 = 180 – 105° = 75°
∠8 = 105°
∴ ∠7 + ∠8 = 180°
∠7 = 180 – 105° = 75°
∠3 = ∠5 = 75°
∠4 = ∠2 = 105°
Question no – (7)
Solution :
If ∠QMD = 100°
There, ∠QMC,
= 180° – 100°
= 80°
∠PLA = 100°
∠PLB,
= 180 – 100
= 80°
∠LMD = 80°
∠CML,
= 180 – 80
= 100°
∠ALM = 80°
Question no – (8)
Solution :
In the question,
Clearly, ∠z = 80°
∴ ∠z = ∠y = ∠x = ∠t = 80°
All are Corresponding angle.
Question no – (10)
Solution :
∠a = 110° – opposite angle,
∠d = 85°
∠d = ∠c = 85°
∠a = ∠b
∠b = 110°
Question no – (11)
Solution :
Let the angle 3x and zx
3x + 2x = 180°
= x = 180/5 = 36
So, ∠1 = 3 × 36 = 108° and ∠2 = 72°
∠1 = ∠5 = 108°
∠2 = ∠6 = 72°
∠4 = ∠6 (corresponding)
∠4 = 72°
∠3 = ∠5 (alternative)
∠3 = 108°
Question no – (12)
Solution :
∠4 = 180° – 60 = 120°
Clearly, ∠4 = ∠1 = ∠2 = 120°
∠3 = 120° (opposite angle)
Question no – (13)
Solution :
In the given question,
∠1 = 60°
∴ ∠3 = 60° (corresponding angle)
= ∠3 + ∠4 = 180°
= ∠4 = 180 – 60 = 120°
= ∠4 = ∠2 (corresponding angle)
∴ ∠2 = 120°
Question no – (14)
Solution :
∠ECD + ∠CEF = 180°
∠ECD = 180 – 130
= ∠ECD = 50°
and ∠BAC = ∠AEC + ∠ECD
= ∠AEC = 70 – 50
= 20°
Therefore, ∠AEC = 20°
Question no – (15)
Solution :
∠1 = ∠3
∠3 = 83°
and ∠3 + ∠2 = 180°
∠2 = 180° – 85
= 95°
Hence, ∠2 = 95°
Question no – (19)
Solution :
Given in the question,
∠x + 125 = 180°
∴ x = 180 – 125
= x = 55°
∴ ∠x + ∠z = 180
= ∠z = 180 – 55°
= ∠z = 125°
∴ ∠x +∠y = 180°
= y = 180 – 55°
= y = 125°
Question no – (20)
Solution :
If we draw are line parallel to PQ || RS
The ∠PXR = QPX = 70°
∠SRX = ∠RXA = 50°
∴ ∠PXR = ∠DXA + ∠RXA
= 50° + 70°
= 120°
Therefore, ∠PXR = 120°
Question no – (21)
Solution :
(i) ∠MLY = 2 ∠LMQ find ∠LMQ.
We know, ∠MLY + ∠LMQ = 180°
= 2 ∠LMQ + ∠LMQ = 180°
= ∠LMQ = 180/3
= 60°
(ii) ∠XLM = (2x – 10)° and ∠LMQ =x + 30°, find x,
∠XLM = VLMQ alternative angles
= 2x – 10 = x + 30°
= x = 30° + 0°
= x = 40°
(iii) ∠XLM = ∠PML, find ∠ALY
We know, ∠LXM + ∠PML = 180°
∠XLM = 90°
Thus, ∠ALY = ∠XLM = 90°
(iv) ∠ALY = (2x – 15)°, ∠LMQ = (x + 40)°, find x
∠ALY = ∠LMS corresponding
2x- 15 = x + 40°
= 2x – x = 40 + 15
= x = 55°
Question no – (22)
Solution :
In the given question,
∠DAB = ∠ABC
∴ x = 40°
And ∠EAC = ∠ACB
∴ y = 55°
Hence, the value of x is 40° and y is 55°
Question no – (23)
Solution :
We know,
y + 32 = 180°
∴ y = 148°
y + ∠BDE = 180°
= ∠BDE = 180 – 148 = 32
∠BED = 18 – 122° = 58
∴ ∠x = 180° – 58 – 32
= x = 90°
So, the angles x 90° is and y is 148°
Question no – (24)
Solution :
In the given question,
∠ABC = 65°, ∠BAC = 55°
∴ ∠ACB = 180° – 55 – 65° = 60°
and ∠ACD = 65 + 55 = 120°
∠ACE = 55° = ∠BAC (alternative)
and ∠ECD = ∠ABC
∴ ∠ECD = 65°
Therefore, ∠ACE = 55°, ∠ECD = 65°, and ∠ACD = 120°
Question no – (26)
Solution :
∠RCB = 180° – 130° = 50°
And x = 180 – 55° – 50°
= 75°
Thus, the value of x is 75°
Question no – (28)
Solution :
= 65 + x = 180 °
= x = 180 ° – 65 ° =115 °
∠A = y = 65 ° and ∠x = yz = 115°
Thus, the value of x = 115°, y = 65°, z = 115°
Question no – (30)
Solution :
As per the question,
∠ABC = ∠DEF
∴ ∠DEF = 75° …(corresponding angle)
Next chapter solution :
👉 Chapter 15 👈