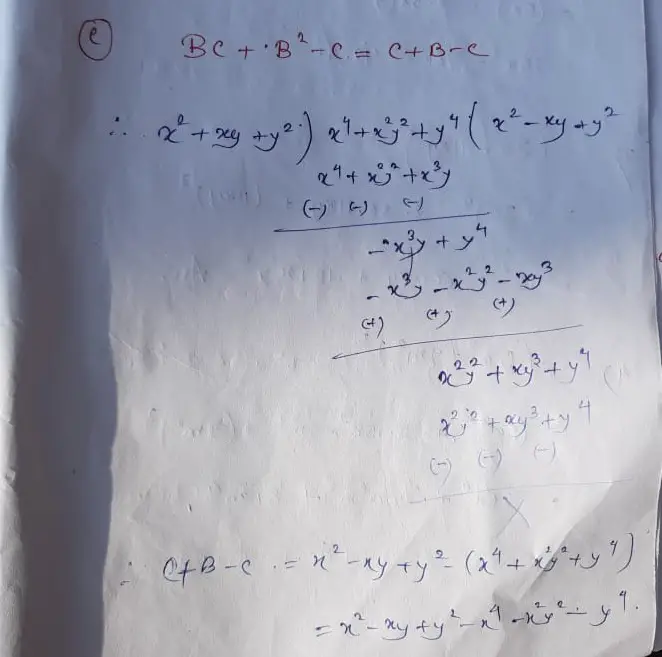NCTB Class 7 Math Chapter Four Exercise 4.3 Solution by Math Expert. Bangladesh Board Class 7 Math Solution Chapter 4.3 “Multiplication & Division of Algebraic Expressions” Exercise 4.3 Solution.
|
Board |
NCTB |
| Class |
7 |
|
Subject |
Math |
| Chapter |
4.3 |
|
Chapter Name |
“Multiplication & Division of Algebraic Expressions” |
| Exercise |
4.3 Solution |
Exercise:- 4.3
(1) Solution:- 3a2 b x (-4ab2)
= – 12 a3 b3 (d)
(2) Solution:- 20 a6b3/4a3 b
= 5 a3 b3(c)
(3) Solution:- – 25x3 y/ 5xy3
= -5x2/y2
(4) Solution:- (8a-2b) + (7a+4b)
= (8×3-2×2) + (-7×3+4×2)
= (24-4) + (-21+8)
= 20-13
= 7.
(5) Solution:- x3+2x2-1
= (-1)3 +{2x (-1)2}
= -1+2-1
= 0
(6) Solution:- 10x6 y5 z4/-5×2 y2 z2
= -2x4 y3 z2
(7) Solution:- (a) (i) & (ii) are correct.
(8) Solution:- ( mx)y
= (m3)2
= m6 Answer (d)
(9) Solution:- a0= 1 (c)
(10) Solution:- x7/x-2
= x9 (a)
(11) Solution:- x- {x- (x-y)}
= x- (x-x +y)
= x-y (c)
(12) Solution:- (x +y) x [x-{x-9x-y)}]
= (x +y) x (x-y)
= x2– y2 (d)
(13) Solution:- a5 x (-a3)0 x a-5
= -a5+3-5
= -a3 (d)
(14) Solution:- [2-{(1+1)-2}]
= 2-{2-2}
= 2
(15) Solution:- 7+2[-8-{-3-(-2-3)}-4]
= 7+2[-8-{-3+5}-4]
= 7+2[-8-2-4]
= 7+2[-14]
= 7-28
= -21
(16) Solution:- -5-[-8-{-4-(-2-3)}+13
= -5-[-8-{-4+5}+13
= -5-[-8-1+13]
=-5-4
= -9
(17) Solution:- 7-2 [-6+3(-5+2(4-3)}]
= 7-2 [-6+3{-5+2×1}]
= 7-2[-6+3x-3]
= 7-2 [-6-9]
= 7-2 (-15)
= 7+30
= 37
(18) Solution:- x-{a+ (y-b)}
= x-(a +y-b)
= x-a-y +b
(19) Solution:- 3x+(4y-z) – {a-b- (2c-4a) -5a}
= 3x+4y-z[a-b-2c+4a-5a}
= 3x+4y-z-[-b-2c]
= 3x+4y-z+b+2c
(20) solution:- -a-[-3b-{-2a-(-a-4b)}]
= -a-[-3b-{-2a+a+4b}]
= -a-[-3b-{-2a+a+4b}]
= -a-{-3b+a-4b}
= -a-{-7b+a}
= 7b-2a
(22) Solution:- {2a-(3b-5c)}-[a-{2b-(c-4a)}-7c]
= {2a-3b+5c}- [a-[2b-c+4a}-7c]
= 2a-3b+5c- [a-2b+c-4a-7c]
= 2a-3b+5c-[-3a-2b-6c]
= 2a-3b+5c+3a+2b+6c
= 5a-b+11c
(23) Solution:- -a+[-6b-{-15c+(-3a-9b-13c)}]
= -a+[-6b-{-15c-3a-9b-13c}]
= -a+[-6b-{-28c-3a-9b}]
= -a+[6b+28c+3a+3b]
= -a+3b+28c+3a
= 2a+3b+28c
(24) Solution:- -2x-[-4y-{-6z-(8x-10y+12z)}]
= -2x-[-4y-{-6z-8x+10y-12z}]
= -2x-[-4y-{-18z-8z-8z-8x+10y}]
= -2x-[-4y+18z+8x-10y]
= -2x-[-14+18z+8x]
= -2x+14y+18z+8x
= -10x+14y-10z
(27) Solution:- 20 –[{( 6a+3b) – (5a-2b)}+6]
= 20-[{(6a+3b-5a+2b}+6]
= 20-[{a+5b}+6]
= 20-[a+5b+6]
= 20-a-5b-6
= 14-a-5b
(29) Solution:- 15a+2[3b+3(2a+2(2a+b)}]
= 15a+2[3b+3 (2a+4 a-2b)}]
= 15a + 2[3b+3 (2a-4 a-2b)}]
= 15a+2[3b-6a-6b]
= 15a+2[-3b-6a]
= 15a-6b-12a
= 3a-6b
(29) Solution:- [8b-3{2a-3(2b+5)-5(b-3)}]-3b
= [8b-3{2a-6b-15-5b+15}]-3b
= [8b-3{2a-11b}]-3b
= [8b-6a+33b]-3b
= 41b-6a3b
= 38b-6a
(30) Solution:- a-b +c-d
= a- (b-c+ d)
(31) Solution:- a-b-c +d-m +n-x +y
= a-(b +c-d)-m+ (n-x) +y
(32) Solution:- 7x-5y+8z-9
1st, 7x-5y- (-8z+9)
2nd, 7x+{-5y-(-8z+9)}
Therefore, 7x+{-5y-(-8z+9)}
(33) Solution:- (a) (15x2+7x-2)- (5x-1)
= 15x2+7x-2-5x+1
= 15x2+2x-1
(b) (15x2+7x-2) x (5x-1)
= 75x3+35x2-10x-15x2-7x+2
= 75x3+20x2-17x+2
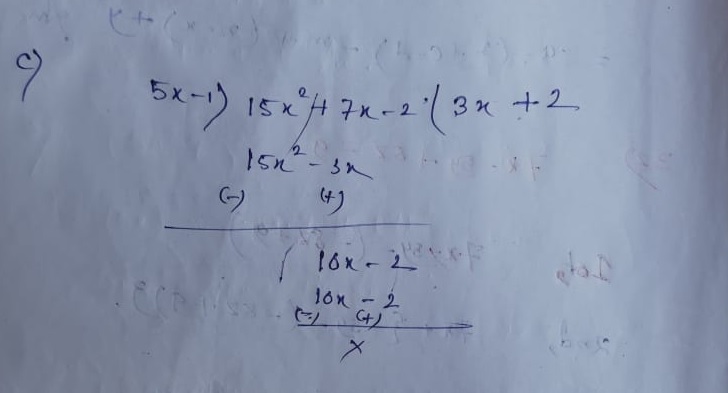
(34) Solution:- (a) A+B
= (x2-xy+y2) + (x2+xy+y2)
= (x2-xy+y2+x2+xy+y2)
= (2x2+2y2)
= 2 (x2+y2)
(b) Solution:- A x B
= (x2-xy+y2) x (x2+xy+y2)
= x4-x3 y+x2 y2+x3y-x2 y2+xy3+ x2 y2– xy3+y4
= (x4+ x2 y2+y4)