Warning: Undefined array key "https://nctbsolution.com/brilliants-composite-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Brilliant’s Composite Mathematics Class 8 Solutions Chapter 1 Squares and Square Roots
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Brilliant’s Composite Mathematics Class 8 Math Book, Chapter 1, Squares and Square Roots. Here students can easily find step by step solutions of all the problems for Squares and Square Roots, Exercise 1.1, 1.2 and 1.3 Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily.
Squares and Square Roots Exercise 1.1 Solution :
Question no – (1)
Answer :
(a) 2
= 22
= 2 × 2
= 4
(b) 21
= 212
= 21 × 21
= 441
(c) 21
= 212
= (20 + 1)2
= 202 + 20 × 12
= 400 + 40 + 1
= 441
(d) 29
= 292
= (30 – 1)2
= 302 – 2 × 30 × 1 + 11
= 900 – 60 + 1
= 641
(e) 111
= 1002 + 2 ×100 × 11 × 112
= 10000 + 2200 + 121
= 12,321
(f) 138
= 1382
= (140 – 2)2
=1402 – 2 × 140 × 2 + 22
= 19600 – 560 + 4
= 19044
(g) 37
= 372
= (40 – 3)2
= 402 – 2 × 40 × 3 + 32
= 1600 – 240 + 9
= 1369
(h) 48
= 482
= (50 – 2)
= 502 – 2 × 50 × 2 + 22
= 2500 – 200 + 4
= 2304
(i) 2/5
= 2/52
= 2/5 × 2/5
= 4/25
(j) 102/300
= 102/3002
= 102/300 × 102/300
= 289/2500
= 0.1156
(k) 0.7
= (0.7)2
= 7/10 × 7/10
= 49/100
= 0.49
Question no – (2)
Answer :
(a) Given number, 16
= 16 = 2 × 2 × 2 × 2 (Perfect square)
(b) 12
= 12 = 2 × 2 × 3 (Not perfect square)
(c) 20
20 = 2 × 2 × 5 (Not perfect square)
(d) 3125
= 3125 = 25 × 25 × 5 (Not perfect square)
(e) 2156
= 2156 = 14 × 14 × 11 (Not perfect square)
(f) 118
= 188 = 2 × 59 (Not perfect square)
(g) 350
= 350 = 5 × 7 × 5 × 2 (Not perfect square)
(h) 1600
= 1600 = 4 × 4 × 10 × 10 (perfect square)
(i) 252
= 252 = 2 × 2 × 3 × 3 × 7 (Not perfect square)
Question no – (3)
Solution :
(a) 25
= √25
= 5 (odd Number)
(b) 121
= √121
= 11 (odd Number)
(c) 64
= √64
= 8
(d) 100
= √100
= 10
(e) 256
= √256
= 16
(f) 1296
= √1296
= 36
(g) 36
= √36
= 6
(h) 6561
= √6561
= 81
Question no – (4)
Solution :
(a) 9
= √9
= 3
(b) 49
= √49
= 7
(c) 36
= √36
= 6
(d) 169
= √169
= 13
(e) 225
= √225
= 15
(f) 900
= √900
= 30
∴ They are the Squares of odd number.
Question no – (7)
Solution :
Given, 22050
= 2 × 5 × 5 × 21 × 21
Since there are only 2 left.
So, if multiplied by 2, it become perfect square.
Question no – (8)
Solution :
Given, 6000
= 10 × 10 × 2 × 2 × 15
∴ If we divide by 15 it become perfect square.
Question no – (9)
Solution :
(a) 182 – 172 = ____
= 182 – 172
= 324 – 289
= 35
(b) 242 – 232 = ____
= 242 – 232
= (24 + 23) (24 – 23)
= 47
(c) 322 – 312 = ____
= 322 – 312
= (32 + 31) (32 – 31)
= 63
(d) 5512 – 5502 = ____
= 5512 – 5502
= (551 + 550) (551 – 550)
= 1101
(e) 1012 – 1002 = ____
= 1012 – 1002
= (101 + 100) (101 – 100)
= 201
(f) 2012 – 2002 = ____
= 2012 – 2002
= (201 + 200) (201 – 200)
= 401
Question no – (10)
Solution :
(a) 552 = ____
= 552
= 55 × 55
= 3025
(b) 752 = ____
= 75 × 75
= 5625
(c) 952 = ____
= (100 – 5)2
= 1002 – 2 × 100 × 5 + 52
= 10000 – 100 + 25
= 9025
Question no – (11)
Solution :
(a) (1, 2, 3)
= 12 + 22
= 1 + 4
= 5 ≠ 32
∴ Not a Pythagorean triplet.
(b) (3, 4, 5)
= 32 + 42
= 9 + 16
= 25 = 52
∴ It is a Pythagorean triplet.
(c) (6, 8, 10)
= 62 + 82
= 36 + 64
= 100 = 102
∴ It is a Pythagorean triplet.
(d) (2, 2, 3)
= 22 + 22
= 4 + 4
= 8 ≠ 32
∴ Not a Pythagorean triplet.
(e) (1, 1, 1)
12 + 12
= 1 + 1
= 2 ≠ 12
∴ Not a Pythagorean triplet.
(f) (6, 7, 8)
= 62 + 72
= 36 + 49
= 85 ≠ 82
∴ Not a Pythagorean triplet.
Squares and Square Roots Exercise 1.2 Solution :
Question no – (1)
Solution :
(a) 100

100 = 2 × 2 × 5 × 5
∴ = √100 = 2 × 5
= 100
(b) 1225

1225 = 5 × 5 × 7 × 7
1225 = 5 × 5 × 7 × 7
∴ = √1225 = 5 × 7
= 35
(c) 625

625 = 5 × 5 × 5 × 5
∴ = √625 = 5 × 5
= 25
(d) 1296
1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
∴ = √1296 = 2 × 2 × 3 × 3
= 36
(e) 144

144 = 2 × 2 × 2× 2 × 3 × 3
∴ = √144 = 2 × 2 × 3
= 12
(f) 9/16
= √9/16
= = √3 × 3/2 × 2 × 2 × 2
= 3/2 × 2
= 3/4
(g) 4096

= 4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ = √4096 = 2 × 2 × 2 × 2 × 2× 2
= 64
(h) 529

= 529 = 23 × 23
∴ = √629
= 23
(i) 144/169
= √144/169
= = √2 × 2 × 2 × 2 × 3 × 3/13× 13
= 2 × 2 × 3/13
= 12/13
(j) 3844/196
= √3844/196
= √2 × 2 × 31 × 31/2 × 2 × 7 × 7
= 2 × 31/2 × 7
= 31/7
Question no – (3)
Solution :
(a) √45 + 4
= √45 + 4
= √45
= √ 7 × 7
= 7 …(Simplified)
(b) √520 + 9
= √520 + 9
= √524
= √23 × 23
= 23 …(Simplified)
(c) √49 + √169/√64 + √49
= √49 + √169/√64 + √49
= 7 + 13/8 + 7
= 20/15
= 4/3 …(Simplified)
(d) √1024 + √529/√4096 + √196
√1024 + √529/√4096 + √196
= 32 + 23/64 + 14
= 55/78 …(Simplified)
(e) √1764 + √400/√16 + √256
= 42 + 20/4 + 16
= 62/20
= 31/10 …(Simplified)
Question no – (4)
Solution :

So, 1100 = 2 × 2 × 5 × 5 × 11
We can see that 2 and 5 have pairs fret 11 doesn’t. So in order to get a perfect square either we have to divide 11.00 by 11 or multiply with 11.
In, first case,
= 1100 ÷ 11 = 100
and √100 = 10
In, second case,
1100 × 11 = 12100
and √12100 = 110
Question no – (5)
Solution :

∴ 9408 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 7 × 7
Clearly, only 3 doesn’t pair.
Therefore, to get a perfect square, we have to divide 9408 by 3.
Question no – (6)
Solution :

Let, the number of students be x
∴ x2 = 4096
∴ x = √4096
∴ x = 64
Now,
∴ 4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 2
∴ √4096 = 2 × 2 × 2 × 2 × 2 × 2
= 64
∴ There were 64 students in the school.
Squares and Square Roots Exercise 1.3 Solution :
Question no – (1)
Solution :
Given numbers, 64, 289, 169, 625, 4096.
√64
= √2 × 2 × 2 × 2 × 2 × 2
= 2 × 2× 2
= 8
√289
= √17 × 17
= 17
√169
= √13 × 13
= 13
√625
= √5 × 5 × 5 × 5
= 5 × 5
= 25
√4096
= √ 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2 × 2 × 2 × 2 × 2× 2
= 64
Question no – (2)
Solution :
(i) 3481

∴ √3481
= 59
(ii) 119025

∴ √119025
= 345
(iii) 152881

∴ √152881
= 391
(iv) 5776

∴ √5776
= 76
Question no – (3)
Solution :
(i) 363609
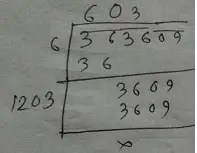
∴ √363609
= 603
(ii) 531441

∴ √ 531441
= 729
(iii) 22801

∴ √22801
= 151
(iv) 998001

∴ √998001
= 999
(v) 18662400

∴ √18662400
= 4320
(vi) 5803281

∴ √5803281
= 2409
(vii) 480249

∴ √480249
= 693
(viii) 63409369

∴ √63409369
= 7977
(ix) 9653449

∴ √9653449
= 3107
(x) 62504836

∴ √62504836
= 7906
Question no – (4)
Solution :

∴ To get a perfect square we have to subtracted 31 and the square root will be 127.
Question no – (5)
Solution :

∴ 464 should be added
Question no – (6)
Solution :

∴ To get a perfect square we have to subtracted 31 and the square root will be 127.
Question no – (7)
Solution :

∴ 489 should be added with 100000 to get a perfect square.
∴ 100489 is the least square number of 6 digits.
Question no – (8)
Solution :

∴ We have to subtract 198
∴ 9999 – 198
= 9801
Question no – (9)
Solution :

∴ There are 85 rows
Question no – (10)
Solution :
(i) 2 23/49
√2 23/49
= √(49 × 2) + 23/49
= √121/49
= √11 × 11/7 × 7
= 11/7
= 1 4/7
(ii) 256/625
= √256/625
= √2 × 2 × 2 × 2 × 2 × 2 × 2 × 2/5 × 5
= 2 × 2 × 2 × 2/5 × 5
= 16/5
(iii) 113 7/9
= √133 7/9
= √1024/9
= √2 v 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2/3 × 3
= 2 × 2 × 2 × 2 × 2/3
= 32/3
(iv) 29 4/25
= √ 29 4/25
= √729/25
= √3 × 3 × 3 × 3 × 3 × 3/ 5 × 5
= 3 × 3 × 3/5
= 27/5
(v) 21 51/169
= √21 51/169
= √3600/169
= √2 × 2 × 2 × 2 × 3 × 3 × 5 × 5/13 × 13
= 2 × 2 v 3 × 5/13
= 60/13
(vi) 21 2797/3364
= √73441/3364
= √ 271 × 271/58 × 58
= 271/58
Question no – (11)
Solution :
(i) 37.0881
∴ √37.0881
= 6.09
(ii) 0.1681
∴ √0.1681
= 0.41
(iii) 7260.7441
∴ √7260.7441
= 85.21
(iv) 1225.6004
Question no – (12)
Solution :
(i) 7
∴ √7
= 2.6457 ≈ 2.646
(ii) 14.01
∴ √14.01
= 3.7429 ≈ 3.743
(iii) 3.14
∴ √3.14
= 1.7708 ≈ 1.771
(iv) 25.6/52.9
= √256 × 10/529 × 10
= √256/529
= 16/23
(v) 71971.145
∴ √71971.145
= 268.2741 ≈ 268.274
Next Chapter Solutions :
| Chapter 2 | Chapter 3 | Chapter 4 | Chapter 5 | Chapter 6 | Chapter 7 |
| Chapter 8 | Chapter 9 | Chapter 10 | Chapter 11 | Chapter 12 | Chapter 13 |
| Chapter 14 | Chapter 15 | Chapter 16 | Chapter 17 | Chapter 18 |