Warning: Undefined array key "https://nctbsolution.com/brilliants-composite-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Brilliant’s Composite Mathematics Class 8 Solutions Chapter 12 Circle
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Brilliant’s Composite Mathematics Class 8 Math Book, Chapter 12, Circle. Here students can easily find step by step solutions of all the problems for Circle, Exercise 12.1, 12.2 and 12.3 Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily.
Circle Exercise 12.1 Solution
Question no – (1)
Solution :
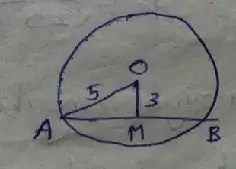
Since, ∆ AMO is a right angular triangle and ∠AMO is the right angle we have, AM2 + MO2 = AO2
Or, Am2 + 32 = 52
Or, AM2 = 25 – 9 = 16
∴ AM = √16 = 4 cm
∴ AB = 2.4 = 8 cm.
Question no – (2)
Solution :
Required Figure,
Here, ∆OCA is a right angular triangle and ∠OCA is the right angle. Here, OC = 6 cm, AC = 1/2 AB = 8cm. we have to find OA By Pythagoras theorem, OA2 = OC2 = AC2
Or, OA2 = 62 + 82 = 36 + 64 =100
∴ OA = √100 = 10
∴ The radius at the circle is 10 cm.
Question no – (3)
Solution :
Required figure,

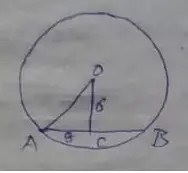
Here, OA = 5 cm, AC = 1/2 AB = 4 cm. ∆OAC is a right angular triangular
Triangle so we have OA2 = OC2 + AC2
Or, OC2 = OA2 – AC2
Or, OC2 = 52 – 32 = 25 – 16 = 9
∴ OC = √9 = 3 cm.
∴ The distance from the center to the chord is 3 cm.
Question no – (4)
Solution :
Required figure,

Here ∆ AOC is a right angular triangle in which AO is the hypogenous.
∴ By Pythagoras theorem we have AO2 = OC2 + AC2
Or, AC2 = AO2 – OC2
Or, AC2 = 132 – 122 = 169 – 144 = 25
∴ AC = √25 = 5 cm.
Question no – (5)
Solution :
Required figure,
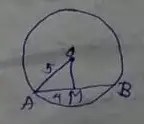
∆AMO is a right angular triangle, where AO is the hypotonus
∴ AO2 = AM2 + MO2
Or, MO2 = AO2 – AM2 = 52 – 42 = 25 – 16 = 9
∴ MO = √9 = 3 cm.
Question no – (6)
Solution :
Required Figure,

AM2 = OA2 – OM2 = 132 – 52 = 169 – 25
Or, AM2 = 144
∴ AM = √144 = 12 cm.
Since, AB = 2AM
∴ AB = 2 × 12 = 24 cm.
Question no – (7)
Solution :
The statement is True.
There are two different ways to think of it.
Firstly, starting from any point on a circle, if we draw a straight line in any direction, then we can observe that it touches at most one another point.
Secondly, if we cut any arc from a circle, then we can find that none of three points among them are colinear.
Question no – (8)
Solution :
Required Figure,

Suppose, AB and CD are two parallel chords. Lets draw a radius OP such that OP || AB || CD.
Since, O is the centre of the circle and E and F are mid-points of AB and CD
∴ ∠AEO = 90°
And, OP || AE ⇒ ∠EOP = 90°……(i)
Also, OP || CD, thus, ∠POF = 90° …..(ii)
From (i) and (ii), we have ∠EOP + ∠POF = 180°
⇒ EOF is a straight line.
Question no – (11)
Solution :
Draw two biggest chords and notice, where do they intersect. That is the centre.
Question no – (12)
Solution :
Required Figure,

AO = 1/2 AB = 3 cm
∴ In △AOM, we have AM² = AO² + OM²
Or, OM² = AM² – AO² = 5² – 3²
Or, OM² = 25 – 9 = 10
∴ OM = √16 = 4 cm
In △ANO, AN = AO + ON
Or, On = AN – AO
Or, ON = 4 – 3
= 16 – 9 = 7
∴ ON = √16 = 2.6 cm
∴ Distance between the centres,
= OM + ON
= 4 + 2.6
= 6.6 cm
Circle Exercise 12.2 Solution
Question no – (1)
Solution :
Required Figure,
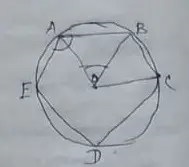
Since, there a re 5 sides and the pentagon is a regular one,
∴ Each of its angle are equal.
And, each of them is equal to 360°/58° = 72°
So, each inner angle = 180° – 72° = 108° = ABC
Since, OB is a bisector of ∠ABC,
∠OBA = ∠OAB = 108/2 = 54°
Now, in △ABO, ∠AOB
= 180° – (54° + 54°)
= 180° – 108°
= 72°
Therefore, each side of a regular pentagon is 72°
Question no – (2)
Solution :
Required Figure,
As we know square is a regular polygon of 4 sides.
So, each outer angle measures
= 360°/4
= 90°
Each inner angle
= 180° – 90°
= 90°
Now, AC is a bisector of ∠DAB
∠OAB = ∠OBA
= 90°/2 = 45°
∠AOB = 180° – (45° + 45°)
= 180° – 90°
= 90°
Therefore, each side will subtend 90° at the centre.
Question no – (3)
Solution :
| Angle | 72° | 36° | 20° | 45° | 30° |
| No of Sides | 360°/72° = 5° | 360°/36° = 10° | 360°/20° = 20° | 360°/45° = 8° | 360°/30° = 12° |
Question no – (4)
Solution :
Measure of each angle subtended at centre
= 360°/9
= 40°
Question no – (5)
Solution :
Measure of each angle subtend at centre,
= 360°/6
= 60°
Circle Exercise 12.3 Solution :
Question no – (1)
Solution :
Required Figure :

Comparing △AOB and △AOC we get,
(i) OAB = OAC [Since, OA = OB = OCC, △OAB, △OAC are isosceles]
(ii) ∠OAB = ∠OCA [Since, OA = OB = OCC, △OAB, △OAC are isosceles]
(iii) OA common side
Therefore, △AOB ≅ △AOC
Question no – (2)
Solution :
Required Figure :

Comparing △MSO and △NSO,
We get,
(i) ∠SNO = ∠SMO [both are right angle]
(ii) ∠OSM = ∠OSN [Given]
(iii) OS is common side.
Thus, △MSO ≅ △NSO ….(Proved)
Since, △MSO ≅ △ NSO, OM = ON …(Proved)
Question no – (3)
Solution :
Required Figure :

Comparing △OPQ and OPR
We have,
(i) ∠OPQ = ∠OPQ [OP is the bisector]
(ii) ∠ORB = ∠OQR [Both are 90]
(iii) OP is common side
∴ △OPQ ≅ △OPR
∴ OR = OQ [Similar sides of equal triangles]
∴ AB = CD [Equidistant chords of a circle]
Question no – (5)
Solution :
Required Figure :

Comparing ∆BOL and ∆BOM, we have,
(i) ∠OLB = COMB
(ii) ∠LBO = ∠ OBM
(iii) OB is common side
∴ ∆DLB2 = ∆OMB
∴ OL = OM
∴ AB = BC
Question no – (6)
Solution :
Required Figure :

Comparing ∆ADO and ∆AED, we have,
(i) ∠DAO = ∠EAO
(ii) ∠ODA = ∠OEA
(iii) AO is the common side.
SO, ∆ADO and ∆AEO are congruent.
∴ OD = OE
∴ AC = AB
Question no – (7)
Solution :
Required Figure :
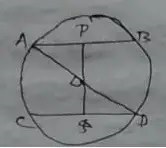
Comparing ∆APO and ∆DQO we have,
(i) OA = OD
(ii) AP = QD
(iii) ∠OPA = ∠OQD
∴ ∆APO2 = ∆DQO
∴ OP = OQ
Question no – (8)
Solution :
Required Figure :

Comparing ∆EFO and ∆EGO, we have,
(i) ∠OFE = ∠OGE
(ii) OF = OG
(iii) OE is common side
∴ ∆OFE2 = ∆OGE
Now, FE = GE
Or, FB + BE = GD + DE
Or, FB + BE = FB + PE
Or, BE = DE (Proved)
Previous Chapter Solution :