Warning: Undefined array key "https://nctbsolution.com/brilliants-composite-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Brilliant’s Composite Mathematics Class 8 Solutions Chapter 7 Compound Interest
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Brilliant’s Composite Mathematics Class 8 Math Book, Chapter 7, Compound Interest. Here students can easily find step by step solutions of all the problems for Compound Interest, Exercise 7.1, 7.2, 7.3, and 7.4 Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily.
Compound Interest Solution Exercise 7.1
Question no – (1)
Solution :
C.I. = 1200 [(1 + 5/100)3 -1 ] = 1200 [(1+1/20)3 -1 ]
= 1200 [(21/20)3 – 1] = 1200 [9261/8000-1]
= 1200 [ 9261 – 8000/8000] = 1200 [1261/8000]
= 3 × 1261/20 = 3783/20

∴ This compound interest is Rs 189.15 rupees .
Question no – (2)
Solution :
C.I. = 1000 [(1 + 4/100)2 – 1 ]
= 1000 [(1+1/25)2 – 1]
= 1000 [(26/25)2 -1]
= 1000 [ 676/625 -1 ]
= 1000 [51/625]
= 8 × 5/25 = Rs 408/5

∴ The compound interest is 81.6 .
Question no – (3)
Solution :
C.I. = 10000 [(1+10/100)3 -1 ] = 10000 [(11/10)3 – 1]
= 10000 [1331/1000 -1] = 10000 [331/1000]
= 10 × 331 = Rs 3310.
Question no – (6)
Solution :
A = 1000 (1+5/100)3
= 1000 (1+1/20) 3
= 1000 (21/20)3
= 1000 × 9261/8000

∴ The amount = Rs 1157.6
Question no – (7)
Solution :
Principal = 5000, interest rate 5%,
∴ Interest for first 6 months = 5000 × 6/12 × 5/100 = 125 rupees
Principal for next 6 months = 5000+125 = 5125 rupees. 1
∴ Interest = 5125 × 6/12 × 5/100
= 205 × 1/2 × 5/4 = 1025/8
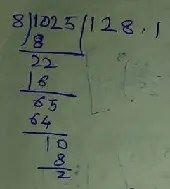
∴ Total interest,
= 125 + 128.1
= 253.1 rupees
Compound Interest Solution Exercise 7.2
Question no – (1)
(i) P = Rs 10000; R = 10% per annum; n = 3
Solution :
Amount = 10000 (1+10/100)3
= 10000 (11/10)3
= 10000 × 1331/1000
= 13310 rupees .
C.I. = Amount – Principal
= 13310 – 10000 = 3310 rupees
Therefore, amount will be Rs 13310 and Compound interest is Rs 3310.
Question no – (3)
Solution :
Principal = 64000, rate of interest = 2.5 paise per rupee = 2.5%
C.I. = 64000 [(1+2.5/100)3 – 1]
= 64000 [(1+1/40)3 – 1]
= 64000 [(41/40)3 -1]
= 64000 [68921/64000 – 1]
= 64000 [68921 – 64000/64000]
= 4921 rupees.
Hence, compound interest payable after 3 years will be Rs. 4921
Question no – (4)
Solution :
C.I. = 1000 [(1 + 3/2×10/100)3 – 1]
= 1000 [(1 + 15/100)3 – 1]
= 1000 [(23/20)3 – 1]
= 1000 [ 12167/8000 – 1]
= 1000 × 4167/-8000
= 4167/8
= Rs 157.62
Thus, the compound interest will be Rs 157.62
Question no – (6)
Solution :
Compound Interest = 15625 [( 1 + 1/4 × 16/100)3 – 1]
= 15625 [(1 + 1/25)3 – 1 ]
= 15625 [(26/25)3 – 1]
= 15625 [17576 – 15625/15625]
= Rs 1951
Therefore, the Compound Interest Rs 1951.
Question no – (10)
Solution :
The first man will pay = 1000 [(1 + 10.5/100)]
= 1000 × 110.5/100 = 1105 rupees
The second man will pay = 1000 [(1 + 1/2 × 10/100)2
= 1000 ( 1 + 5/100)2
= 1000 × 441/400
= 441 × 2.5 = 1102.5 rupees,
∴ 1105 b- 1102.5 = 2.5 rupees .
Therefore, the first person will pay 2.5 rupees more
Question no – (12)
Solution :
Compound interest = 12000 [(1 + 9/100 )2 – 1 ]
= 12000 [(109/100)2 -1 ]
= 12000 × 1881/10000
= 6 × 1881/8 = 1881 × 1.2 = 2257.2
S.I = 12000 × 9 × 2 /100 = 2160 rupees
∴ Difference,
= 2257.2 – 2160
= 97.2 rupees
Hence, the difference will be Rs 97.2.
Compound Interest Solution Exercise 7.3
Question no – (1)
Solution :
As per the question,
Amount = 164, rate = 5%, period = 2 years
∴ P (1 + 5/100)2 = 0164
Or , P (21/20)2 = 164
Or, P = 164 × 400/441
∴ P = 148.75
Question no – (2)
Solution :
P [(1 + 10/100)3 – 1] = 331
Or, P [(11/10 )3 – 1] = 331
Or, P [331/1000] = 331
Or, P = 331 × 1000/331
∴ P = Rs 1000
Question no – (3)
Solution :
1200 (1 + 5/100)n = 1323
Or, 1200 × (21/20)n = 1323
Or, ( 21/20)n = 1323/1200
Or, (21/20)n = 441/400 = (21/20)2
∴ n = 2
Question no – (4)
Solution :
64000 (1 + 1/2 × 5/100)2 = 68921
Or, 64000 (41/40)n = 68921
Or, (41/40)n = 68921/69000
Or, (41/40)n = (41/40)3
∴ n = 3
Question no – (5)
Solution :
800 (1 + 5/100)n = 882
Or, 800 (21/20)n = 882
Or, (21/20)n = 882/800
Or, (21/20 )n = 441/400
= (21/20)2
∴ n = 2
Question no – (6)
Solution :
2000 (1 + 1/2 × r/100)3 = 2315.25
Or, (1 + r/200)3 = 2315.25/2000
Or, (200 + r/200)3 = 1157.375/1000
Or, 200 + r/200 = 3√1157.375/1000
Or, 200 + r/200 = 10.5/10
Or, 10r + 2000 = 2100
Or, 10r = 100
Or, r = 10%
Question no – (7)
Solution :
1000 (1 + r × 1/2/100)12 = 2012.2
Or, (1 + r/200)12 = 2012.2/1000
Or, (1+r/200)12 = 2.012
Or, 1 + r/200 = 12√2.012
∴ r = (12√2.012 – 1) × 200
Question no – (8)
Solution :
5000 (1 + r × 1/2/100)10 = 10000
Or, (1 + r/200)10 = 10000/5000 = 2
Or, (1 + r/200) = 2
Or, 1 + r/200 = 10√2 = 1.072
Or, r/200 = 0.072
Or, r = 14.4%
Question no – (9)
Solution :
P (1 + (r/2) /100)3 = 9826
Or, P (1 + ( 5/4 )/100)3 = 9826
Or, P (1 + 1/80)3 = 9826
Or , P (81/80)3 = 9826
Or, P = 9826 × 80 × 80 × 80 / 81 × 81 × 81
Question no – (10)
Solution :
4400 (1 + 8/100)n = 4576
Or, (108/100)n = 4576/4400
Or, (27/20)n = 104/100
Or, (27/25)n = 26/25
Question no – (11)
Solution :
64000 (1 + ( 5/2 )/100)n = 68921
Or, 64000 (41/40)n = 68921
Or, (41/40)n = 68921/69000
Or, (41/40)n = (41/40)3
∴ n = 3
∴ The required period is = (6 × 3) = 18 months .
Question no – (12)
Solution :
10000 (1 + r/100)3 = 13310
Or, (1 + r/100)3 = 13310/10000 = 1331/1000
Or, (1 + r/100) =3√ 1331/1000 = 11/10
Or, r/100 = 11/10 – 1 = 1/10
∴ r = 10%
Question no – (13)
Solution :
2000 (1 + ( r/2)/100)3 = 2662
Or, (1 + r/200)3 = 2662/2000 = 1331/1000
Or, (1 + r/200 )3 = ( 11/10 )3
Or, 1 + r/200 = 11/10
Or, r/200 = 11/10 – 1 = 1/10
Or, r/200 = 1/10
Or, r = 20%
Question no – (14)
Solution :
Let the sum be P, then the amount will be 2p
∴ p ( 1 + r/100 )3 = 2p
Or, ( 1 + r/100 )3 = 2
Or, ( 1 + r/100 ) = 3 √ 2
Or, r = ( √2 – 1 ) × 200
Question no – (15)
Solution :
Let the sum be P
P ( 1 + ( 12.5/2 )/100 )3 = 4913
Or, P ( 17/16 )3 = 4913
Or, P = 4913 × 16 × 16 × 16/17 × 17 × 17
Or, P = 16 × 16 × 16 = 4096 rupees
Question no – (16)
Solution :
Let the sum be P
P [(1 + 10/100)2 – 1] – p × 10 × 2/100 = 500
Or, P [ 21/100 ] – p/5 = 500
Or, 21 p – 20 p/100 = 500
Or, p= 500 × 100 = 50000 rupees
Question no – (17)
Solution :
Interest on 7396 in 1 year
= 7950.70 – 7396
= 554.70 rupees
∴ rate of interest,
= 554.70/7396 × 100
= 15/2
= 7 1/2%
Compound Interest Solution Exercise 7.4
Question no – (1)
Solution :
Population after two years
= 16000 ( 1 + 5/100 )2 = 16000 ( 21/20 )2
= 16000 × 441/400
= 40 × 441
= Rs 17640
Question no – (2)
Solution :
Population after 2 years = 80000 ( 1 + 75/1000 )2
= 8000 (43/40 )2 = 8000 × 43 × 43/1000
= 5 × 1849
= Rs 9245
Question no – (3)
Solution :
Value after 2 years = 1,00,000 ( 1 – 10/100 )2 = 10000 ( 9/10 )2
= 100000 × 81/100 = 81000
∴ Deprecation = 100000 – 81000
= Rs 19000
Question no – (4)
Solution :
Value after 3 years = 7812.50 ( 1 – 12/100 )3 = 7812.50 × ( 22/25 )3
= 7812.5 × 22 × 22/25 × 25 × 25 = 5324
∴ Depreciation = 7812.50 – 5324
= 2488.50
Question no – (6)
Solution :
Final income = 32000 × (1 – 5/100) (1 + 10/100) (1 + 12.5/100)
= 32000 × 19/20 × 11/10 × 9/8
= 20 × 19 × 11 × 9 = 37620
∴ Profit = 37620 – 32000
= 5620 rupees
Question no – (8)
Solution :
Population after 2 years = 490000 ( 1 + 4/100 ) ( 1 + 3/100 )
= 490000 × 26/25 × 103/100 = 196 × 103
= 20188 × 26
= Rs 604888
Question no – (9)
Solution :
Let the previous value be x rupees .
x (1 – 10/100)3 =7290
Or, x (9/10)3 = 7230
Or, x = 7290 × 1000/729
Or, x = 10000 rupees
Question no – (12)
Solution :
Count of bacteria after 3 hours = 1312500 (1 + 10/100) (1 – 8/100) (1 + 12/100)
= 1312500 (11/10) (23/25) (28/25)
= 210 × 11 × 23 × 28
= Rs 1483240
Question no – (14)
Solution :
Population = 72000 (1 + 7/100) (1 – 10/100) = 72000 (107/100) (9/10)
= 72 × 107 × 9
= 648 × 107
= Rs 69336
Question no – (15)
Solution :
Final in come = 160000 (1 + 5/100) (1 + 10/100) (1 + 12.5/100)
= 160000 (21/20 (11/10) (9/8)
= 21 × 11 × 9 × 100 = 207900
∴ Profit = 207900 – 160000
= Rs 47900
Question no – (16)
Solution :
Since, annual birth rate = 3.3% and annual death rate 1.3%
∴ Population is increase by (3.3 – 1.3) = 2%
∴ Population after 3 years = 125000 (1 + 2/100 )3
= 125000 51 × 51 × 51/50 × 50 × 50
= 51 × 51 × 51
= 2601 × 21
= 132651
Therefore, the population after 3 years will be 132651.
Previous Chapter Solution :