Brilliant’s Composite Mathematics Class 8 Solutions Chapter 5

Warning: Undefined array key "https://nctbsolution.com/brilliants-composite-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192

Brilliant’s Composite Mathematics Class 8 Solutions Chapter 5 Division of Algebraic Expressions

Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Brilliant’s Composite Mathematics Class 8 Math Book, Chapter 5, Division of Algebraic Expressions. Here students can easily find step by step solutions of all the problems for Division of Algebraic Expressions, Exercise 5.1 and 5.2 Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily.

Division of Algebraic Expressions Exercise 5.1 Solution

Question no – (1)

Solution : 

Given, x – 4/x³ – 64

= (x – 4)/(x – 4) (x² + 4x + 16)

= 1/x² + 4x 16

Question no – (2) 

Solution : 

Given, 64y³ – 1000/ 8y – 20

= (4y)³ – (10)³/2(4y – 10)

= (4y – 10) (10y² + 40y + 100) / 2(4y – 10)

= 16y² + 40y + 100 / 2

= 2(8y² + 20y + 50) / 2

= 8y² + 20y + 50

Question no – (3) 

Solution : 

As per the question we get,

x² + 5x + 6/x² – 9

= x² + 3x + 2x + 6 / (x +3)(x – 3)

= (x + 3)(x + 2) / (x +3)(x – 3)

= x + 2 / x – 3

Question no – (4) 

Solution :  

According to the question, x² + 7x + 12/ x + 3

∴ x² + 4x  + 3x + 12/ x + 3

= (x + 4) (x + 3) / (x + 3)

= (x + 4)

Question no – (5) 

Solution : 

Given, 2y³ + 2y² – 24y/y³ + 2y² – 8y

= 2y (y² + y – 12)/y(y² + 2y – 4)

= 2(y² + 4y – 3y – 120/(y² + 4y – 2y – 4)

= 2[(y + 4)(y -3)]/(y + 4)(y – 2)

= y – 3/y – 2

Question no – (6) 

Solution : 

Given, x² – 25/x³ – 125

= (x – 5) (x + 5)/(x – 5) (x² + 5x + 25)

= x + 5 / x² + 5x + 25

Question no – (7) 

Solution : 

As per the question, x² – y²/x + y

= (x + y)(x – y)/(x + y)

= (x – y)

Question no – (8) 

Solution : 

Given, 27x³ + y³/9x² – 3xy + y²

= (3x)³ + (y)³/9x² – 3xy + y²

= (3x + y)(9x² – 3xy + y²)/(9x² – 3xy + y²)

∴ (3x + y)

Question no – (9) 

Solution : 

Given, 16x² – 9/4x – 3

= (4x + 3)(4x – 3)/(4x – 3)

= (4x + 3)

Division of Algebraic Expressions Exercise 5.2 Solution

Question no – (1) 

Solution : 

As per the question we know, Dividend = Divisor+ Remainder

Given, 9x² – 24x + 16 by 3x – 4

∴ Quotient = (3x – 4),

∴ Remainder = 0

Question no – (2) 

Solution : 

Given, 9x³ + 3x² – 5x + 7 by 3x – 1

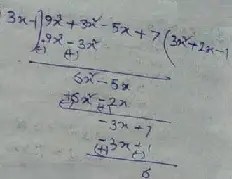
Therefore,

The quotient is = (3×2 + 2x – 1),

Ans the remainder is = 6

Question no – (3) 

Solution : 

As per the question, x² + 7x + 12 by x + 3.

Now,

∴ Quotient = (x + 4),

∴ Remainder = 0

Question no – (4) 

Solution : 

Given, 6x⁵ + 4x⁴ – 27x³ – 7x² – 27x – 6 by 2x² – 3

Now,

∴ Quotient = (3x³ + 2x² – 6x – 1/2),

∴ Remainder = (- 45x – 71/2)

Question no – (5) 

Solution : 

Given, – 10y³ – 2x² – 5x – 1 by 4x + 1

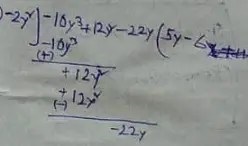
∴ Quotient is = (5y – 6),

∴ Remainder is = (- 22y)

Question no – (6) 

Solution : 

As per the question, -1 by x – 2

Now,

∴ Quotient = (x2 + 2x + 4),

∴ Remainder = 7

Question no – (7) 

Solution : 

Given, 8x³ – 2x² – 5x – 1 by 4x + 1

∴ Quotient = (2x² – x – 1),

∴ Remainder = 0

Question no – (8) 

Solution : 

Given, x⁵ – 94x by x² + 9x

Now,

∴ Quotient is = (x³ – 9x² + 81x – 729),

∴ Remainder is = + 6467x

Question no – (9) 

Solution : 

Given, 2x⁵ + 10x⁴ + 6x³ + x² + 5x + 3 by 2x³ + 1

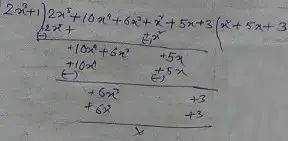
∴ Quotient = x² + 5x + 3

∴ Remainder = 0

Question no – (10) 

Solution : 

Given, 14x³ – 5x² + 9x – 1 by 2x – 1

Now,

∴ Quotient = (7x² + x + 5),

∴ Remainder = 4

Question no – (11) 

Solution : 

According to the given question,

x³ + 7x + 9 by x – 2

Now,

∴ Quotient is = (x² + 2x + 11),

∴ Remainder is = (31)

Question no – (12) 

Solution : 

Given, 27x³ + 1 by 9x² – 3x + 1

∴ Quotient is = (3x + 1),

∴ Remainder is = 0

Question no – (15) 

Solution : 

Given, x³ – 6x² + 11x – 6 by x² + x³

Now,

∴ Quotient = (x – 2)

∴ Remainder = 0

Question no – (16) 

Solution : 

According to the given question,

x⁴ + x² + 1 by x² + x 1

Now,

∴ Quotient is = (x² – x + 1)

∴ Remainder is = 0

Question no – (17) 

Solution : 

As per the given question,

∴ Quotient = (x² – x – 2),

∴ Remainder = 0

Since, Remainder = 0, (x – 3) is a factor of (x³ – 4x² + x + 6)

Question no – (20) 

Solution : 

∴ (14x – 10) must be subtracted from (8x⁴ + 14x³ – 2x² + 7x – 8) to get a divisible polynomial by (4x² + 3x – 2).

Question no – (21) 

Solution : 

According to the question,

Since, remainder ≠ 0,

Therefor (x² + 1) is not a factor of (x⁵ – x⁴ + 3x³ + 4x² + 4x + 6)

Question no – (22) 

Solution : 

As per the question,

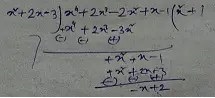
∴ The term, which have to added is,

= {(x² + 2x – 3) – (- x + 2)}

= {x² + 2x – 3 + x – 2}

= x² + 3x – 5

Question no – (24) 

Solution : 

According to the question,

Now, the term (x4 + x3 + 8×2 + ax b) will be divisible by (x2 + 1) if the remainder = (a – 1) = 0 and (b – 7) = 0

⇒ a = 1 and b = 7.

Previous Chapter Solution : 

👉 Chapter 4