Rd Sharma Solutions Class 7 Chapter 20 Mensuration – I Perimeter and the area of rectilinear figures
Welcome to NCTB Solution. Here with this post we are going to help 7th class students for the Solutions of Rd Sharma Class 7 Mathematics, Chapter 20, Mensuration I (Perimeter and the area of rectilinear figures). Here students can easily find Exercise wise solution for chapter 20, Mensuration – I (Perimeter and the area of rectilinear figures). Students will find proper solutions for Exercise 20.1 and 20.2. Our teachers solved every problem with easily understandable methods so that every students can understand easily. Here all solutions are based on the CBSE latest curriculum.
Mensuration – I (Perimeter and the area of rectilinear figures) Exercise 20.1 Solution
Question no – (1)
Solution :
(i) Given in the question,
Length = 5.5 m,
Breadth = 2.4 m
As we know that,
Area of rectangle = Length × Breadth
∴ Area of the rectangle,
= 5.5 × 2.4
= 13.2 m²
Therefore, Area of the rectangle of 13.2 m²
(ii) Given in the question,
Length = 180 cm,
Breadth = 150 cm
∴ Area of the rectangle,
= 180 × 150
= 27000 cm²
Hence, Area of the rectangle of 27000 cm²
Question no – (2)
Solution :
(i) In the given question,
Side = 2.6 cm
As we know that,
Area of a Square = Side × Side
∴ Area of square,
= (2.6)²
= 6.76 cm²
Hence, the area of the square will be 6.76 cm²
(ii) In the given question,
Side = 1.2 dm
∴ Area of the square
= (1.2)²
= 1.44 dm²
Thus, the Area of square will be 1.44 dm²
Question no – (3)
Solution :
Given in the question,
Side = 16.5 dam
∴ Area of the square,
= (16.5)² …(Area of a Square = Side × Side)
= 272.25 dm²
Therefore, the area of a square will be 272.25 dm²
Question no – (4)
Solution :
(i) From the given question,
Length = 200 m
Breadth = 125 m
We know, Area of rectangle = Length × Breadth
∴ Area of the rectangle,
= 125 × 200
= 250 m²
Thus, the Area of rectangle will be 250 m²
(ii) From the given question,
Length = 75 m 5 dm
Breadth = 120 m
∴ Area of the rectangle,
= 75.5 × 120 …(Area of rectangle = L× B)
= 9060 m²
Hence, the Area of rectangle will be 9060 m²
Question no – (5)
Solution :
(i) According to question,
Length = 125 m
Breadth = 400 m
As we know that,
Area of rectangle = Length × Breadth
∴ Area of the field,
= 125 × 400
= 50,000 m²
Thus, the area of the rectangle will be 50,000 m²
(ii) In the given question,
Length = 75 m 5 dm
Breadth = 120 m
∴ Area of the field,
= 75.5 × 120…(Area of rectangle = Length × Breadth)
= 9060 m²
Therefore, the area of the rectangle will be 9060 m²
Question no – (6)
Solution :
As per the given question,
Dimensions = 3 m × 2m and 10 m × 10m
∴ Area of the door,
= 3 × 2
= 6 m²
∴ Area of the wall,
= 10 × 10
= 100 m²
∴ Area to be painted wall,
= 100 – 6
= 94 m²
∴ Total cost for painting,
= 94 × 2.50
= 235
Therefore, the cost of painting will be 235 Rs.
Question no – (7)
Solution :
Let, each side be x cm
∴ Perimeter of rectangle = Perimeter of square
= 2 (40 + 22) = 4 × x
= x = 2 × 62/4
= x = 31
∴ Measure of each side,
= (31)²
= 961 cm²
Question no – (8)
Solution :
First, we find Area of pane,
= 25 × 16
= 400 cm²
Now, the total area of the window,
= 12 × 400
= 4800 cm²
= 0.48 m²
Hence, the window will required 0.48 m² glass.
Question no – (9)
Solution :
In the given question,
Marble tile measures = 10 cm × 12 cm
Wall of size = 3 m × 4 m
First we find area of tile,
= 10 × 12
= 120 cm²
Now, Area of wall,
= 3 × 4
= 12 cm²
∴ We need = 12 m² /120 m²
= 12 × 10000/120
= 1000 tiles
∴ Total cost for tiles,
= 1000 × 2
= 2000 Rs
Therefore, the total cost of the tiles will be 2000 Rs.
Question no – (10)
Solution :
As per the given question,
Length = 9 dm 5 cm
Breadth = 6 dm 5 cm
∴ Area of the table,
= 95 × 65
= 6175 cm²
∴ Total cost for polishing,
= 6175 × 20
= 1235
Hence, the cost of polish will be 1235 Rs.
Question no – (11)
Solution :
According to the question,
Length of room = 9.68 m 6.2 m
Breadth of room = 6.2 m
And, Length of tile = 22 cm
Breadth of tile = 10 cm
∴ Area of the room,
= 9.68 × 6.2
= 60.016 m²
∴ Area of the rectangle tile,
= 22 × 10
= 220 cm²
∴ Total no of tiles,
= 60.016 m²/220 cm²
= 6000160/220
= 2728
∴ Total cost for tiles,
= 2.50 × 2728
= 6820
Hence, total cost of the tiles is 6820 Rs.
Question no – (12)
Solution :
Area of the field,
= (179)²
= 32041 m²
∴ Then total cost for raising a lawn,
= 1.50 × 32041
= 48,061.50
Therefore, the cost of raising a lawn on the field will be 48,061.50 Rs.
Question no – (14)
Solution :
As per the given question,
Corridor of a school = 8 m long and 6 m wide
Canvas sheets = 2 m × 1 m
∴ Area of the corridor,
= 8 × 6
= 48 m²
∴ Area of canvas sheet,
= 2 × 1
= 2 m²
∴ Total no of sheets,
= 48/2
= 24
∴ Cost for canvas sheets,
= 24 × 8
= 192
Therefore, the cost of canvas sheets is 192 Rs.
Question no – (15)
Solution :
As per the question,
Playground = 62 m 60 cm and 25 m 40 cm
∴ Area of the play ground,
= 62.60 × 25.4
= 1590.04
∴ Cost of turfing,
= 2.5 × 1590.04
= 3975
Thus, the cost of turfing will be 3975 Rs.
Question no – (16)
Solution :
According to the question,
lane = 180 m long, 5 m wide
Bricks = length 20 cm, breadth 15 cm
∴ Area of lane,
= 5 × 180
= 900 m²
∴ Area of lane bricks,
= 20 × 15
= 300 cm²
Total no of bricks need,
= 900 m²/300 cm²
= 90000/300
= 30000
= 30 thousand
∴ Total cost,
= 750 × 30
= 22,500
Therefore, the cost of bricks that are required will be 22,500 Rs.
Question no – (17)
Solution :
Given in the question,
Sheet of paper = 125 cm by 85 cm
1 envelope required paper = 17 cm by 5 cm
∴ Area of sheet,
= 125 × 85
= 10,625 cm²
∴ Area of piece paper,
= 17 × 5
= 85 cm²
∴ No of envelope required,
= 10,625/85
= 125
Therefore, total 125 envelopes can be made.
Question no – (18)
Solution :
Let length = L
The area of cloth = 170L cm²
and total area for each diapers,
= 50 × 17
= 850 cm²
Then Given,
= 170L/850 = 25
= L = 25 × 850/170
= 125 cm
Therefore, 125 cm cloth will required to make 25 diapers.
Question no – (19)
Solution :
Given, Carpet for a room = 6.6 m by 5.6 m
∴ Area of the mean,
= 6.6 × 5.6
= 36.96 m²
Total cost given = 3960
∴ Cost of carpet metre,
= 3960/39.96 × 0.7
= 75 Rs.
Therefore, the cost of the carpet per metre will be 75 Rs.
Mensuration – I Exercise 20.2 Solution
Question no – (1)
Solution :
According to the question,
Grassy lawn measure = 40 m by 25 m
∴ Area of the grassy land,
= 40 × 25
= 100 m²
∴ Area of land with a path,
= 44 × 29
= 1276 m²
Then area of the path,
= (1276 – 1000)
= 276 m²
∴ Cost for leveling,
= 8.25 × 276
= 2277
Therefore, the cost of leveling the path will be 2277 Rs.
Question no – (2)
Solution :
Area of the grass with path,
= (30)²
= 900 m²
Area of the garden without path,
= (28)²
= 784 m²
Let rate per square = x
∴ Total cost,
= Area of garden x rate
= 1176 = 784 × x
= x = 1176/784
= 1.50
Hence, the rate per square metre will be 1.50 Rs.
Question no – (3)
Solution :
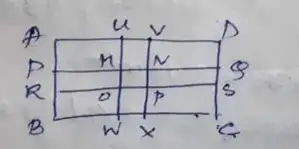
Area of the field,
= 90 × 60
= 5400 m²
Area of PQRS,
= 90 × 3
= 270 m²
Area of UVWX,
= 60 × 3
= 180 m²
Area of MNOP,
= 3 × 3
= 9 m²
∴ Total are of path,
= (270 + 180)
= 441 m²
Therefore, the total area covered by the two roads will be 441 m².
Question no – (4)
Solution :
As per the question,
Sheet of tin = 100 cm by 80 cm
Squares of side = 10 cm from each corner
∴ Area of rectangular sheet of tin,
= 100 × 80
= 8000 cm²
∴ Area of square of sheet,
= 10 × 10
= 100
∴ Total area of side square,
= 4 × 100
= 400 cm²
∴ Area of the remaining sheet,
= 8000 – 400
= 7600 cm²
Therefore, the area of the remaining sheet will be 7600 cm².
Question no – (5)
Solution :
According to the question,
Painting = 8 cm long and 5 cm wide
∴ Area of the cardboard,
= 8 × 5
= 40 cm²
New length,
= 8 – (1.5 + 1.5)
= 5 cm
New breadth,
= 5 – (1.5 + 1.5)
= 2 cm
∴ The area,
= 5 × 2
= 10
∴ Area of margin,
= 40 – 10
= 30 cm²
Therefore, the total area of the margin will be 30 cm².
Question no – (6)
Solution :
As per the given question,
Rakesh field = length 80 m and breadth 60 m
Garden = 10 m long and 4 m broad
Total area of field,
= 80 × 60
= 4800 m²
Area of garden,
= 10 × 4
= 40 m²
Area of bed,
= 4 × 1.5
= 6 m²
Total area for two beds,
= 6 × 2
= 12 m²
∴ Remaining area,
= 4800 – (12 + 40)
= 4748 m²
1 are = 100 m²
∴ 4748 m² = 47.48 areas
∴ Cost of applying manure,
= 300 × 47.48
= 14244
Therefore, the cost of applying the manures will be 14244 Rs.
Question no – (7)
Solution :
According to the question,
Each side of a square flower bed = 2 m 80 cm
Extended by digging a strip = 30 cm
∴ Area for flower bed,
= (2.80)²
= 7.84 m²
New side of flower bed,
= 2.80 + 0.3 + 0.3
= 3.4 m
Then area for flower bed,
= (3.4)²
= 11.56 m²
∴ Increase area of flower bed,
= 11.56 – 7.84
= 3.72 m²
Question no – (9)
Solution :
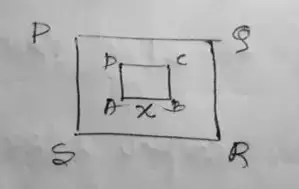
Let, side be x
The area of lawn = x²
and area of PQRS,
= (x + 2 + 2)
= (x + 4)²
Then, (x + 4)² – x² = 136
= x² + 8x + 16 – x² = 136
= 8x = 136 – 16
= x = 120/8
= x = 15
∴ Area of lawn,
= (15)²
= 225 m²
Therefore, the area of the lawn will be 225 m².
Question no – (10)
Solution :
As per the question,
Poster of size = 10 cm by 8 cm
∴ Area of posted,
= 10 × 8
= 80 cm²
∴ Area of cardboard,
= (10 + 1.75 + 1.75) × (8 + 1.75 + 1.75)
= 13.5 × 11.5
= 155.25 cm²
(i) Area of margin,
= 155.25 – 80
= 75.25 m²
(ii) Cost,
= 60× 155.25
= 93.15 Rs.
Question no – (11)
Solution :
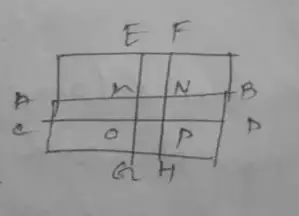
Area of the rectangle,
= 50 × 40
= 2000 m²
Area ABCD,
= 50 × 1.8
= 90 m²
Area EFGH,
= 40 × 2.5
= 100 m²
Area of MNOP,
= 2.5 × 1.8
= 4.5
∴ Then total area of need,
= (100 + 90) – 4.5
= 185.5
∴ Area of the remaining field,
= 200 – 185.5 m²
= 1814.5 m²
Question no – (13)
Solution :
In the given question,
hall = 22 m long and 15.5 m broad
∴ Area of the sheet hall,
= 22 × 15.5
= 341 m²
∴ Area of the carpet,
= (22 – 2 × 0.75) × (15.5 – 0.75)
= 20.5 × 14
= 287 m²
∴ Area of strip,
= 341 0 287
= 54 m²
Question no – (14)
Solution :
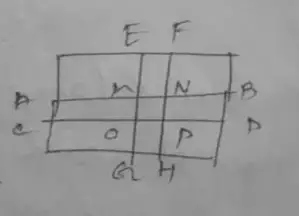
∴ Area of the park,
= 70 × 45
= 3150 m²
Area of ABCD,
= 70 × 5
= 350 m²
Area of EFGH,
= 45 × 5
= 225 m²
Area of MNOP,
= 5 × 5
= 25
Area of roads,
= (350 + 225) – 25
= 530 m²
∴ Cost for constructing roads,
= 550 × 105
= 57,750
Question no – (16)
Solution :
Let, side of lawn = x
Area of lawn = x²
With path area of lawn,
= (x + 2.5 + 2.5)²
= (x + 5)²
Then, x² = (x + 5)² – 165
= x² = x² + 10x + 25 – 165
= 10x = 140
= x = 14
Then side = 14x
∴ Area of law,
= (14)²
= 196 m²
Therefore, the area of the lawn will be 196 m²
Mensuration – I Exercise 20.4 Solution
Question no – (1)
Solution :
(i) In the given question,
Base = 18 cm,
Altitude = 3.5 cm
∴ Area triangle,
= 1/2 × 18 × 3.5
= 31.5 cm²
Therefore, the area will be 31.5 cm²
(ii) In the given question,
Base = 8 dm,
Altitude = 15 cm
∴ Area of triangle,
= 1/2 × 80 × 15
= 60 cm²
Hence, the area will be 60 cm².
Question no – (2)
Solution :
Let altitude = x
The 42 = 1/2 × x × 14
= x = 42 × 2/14
= x = 7
∴ Altitude = 7 cm
Therefore, the altitude of the triangle will be 7 cm.
Question no – (3)
Solution :
As per the given question,
Area of triangle = 50 cm².
Altitude = 8 cm,
Base = ?
We know that,
Altitude = 2 × area/base
∴ 2 × 50/8
= 12.5 cm
Therefore, the base is 12.5 cm.
Question no – (4)
Solution :
According to the question,
Right angle are of lengths = 20.8 m and 14.7 m
∴ Area of triangle,
= 1/2 × 20.8 × 14.7
= 152.88 m²
Therefore, the area of a right angled triangle is 152.88 m².
Question no – (6)
Solution :
As per the given question,
rectangular field = 48 m long ad 20 m wide
right angle measure = 12 m and 5 m can
∴ Area of rectangular field,
= 48 × 20
= 960 m²
∴ Area of triangular flower bed,
= 1/2 × 12 × 5
= 30 m²
∴ No of right triangular flower beds contains,
= 960/30
= 32
Therefore, there are 32 such triangular flower bed.
Question no – (7)
Solution :
Area of △ ADC
= 1/2 × 84 × 16.5
= 693 cm²
Area of △ABC
= 1/2 × 84 × 12
= 504 cm²
∴ Area of ABCD,
= 693 + 504 cm²
= 1197 cm²
Therefore, the area of the quadrilateral ABCD will be 1197 cm².
Question no – (8)
Solution :
As per the given question,
Measure = 48 m and 32 m
∴ Area of quadrilateral,
= 1/2 × 48 × 32 m²
= 768 m²
Therefore, the area of the quadrilateral ABCD will be 768 m².
Question no – (9)
Solution :
Area of rectangle ABCD,
= 32 × 18
= 576 m²
∴ Area of remaining land,
= 576 – 126 m²
= 450 m²
Therefore, the area of the shaded region will be 450 m².
Question no – (10)
Solution :
Required figure,
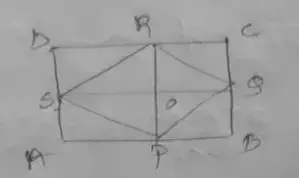
Then OP,
= 25/2
= 12.5
Then area of SRQ,
= 1/2 × 40 × 12.5
= 250 cm²
Then area of PQRS,
= 2 × 250
= 500 cm²
Therefore, Area of the shaded region will be 500 cm².
Question no – (11)
Solution :
First, Area of △ABC,
= 1/2 × 28 × (42 – 12)
= 1/2 × 28 × 30
= 420 cm²
Now, Area of △ABC
= 1/2 × 28 × 12
= 168 cm²
∴ Area of quadrilateral,
= 420 × 168
= 588 cm²
Therefore, the area of the quadrilateral ABCD will be 588 cm².
Question no – (14)
Solution :
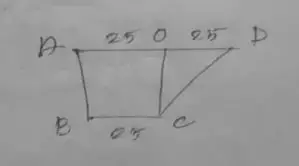
First, Area a ABCD,
= 25 × 30
= 750 m²
Now, Area of COD,
= 1/2 × 25 × 30
= 375 m²
∴ Area of ABCD
= 750 + 375
= 1125 m²
Therefore, the area of quadrilateral field ABCD will be 1125 m².
Question no – (15)
Solution :
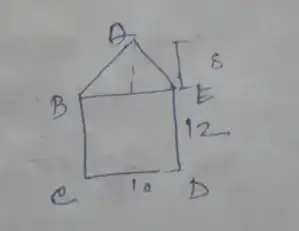
First, we need to find the Area of ABE,
= 1/2 × 10 × 8
= 40 cm²
Now, we find Area of BCDE,
= 10 × 2
= 120 cm²
∴ Area of ABCDE,
= 120 + 40
= 160 cm²
Therefore, the area of the pentagon ABCDE will be 160 cm².
Next Chapter Solution :
👉 Chapter 21 👈