Rd Sharma Solutions Class 7 Chapter 16 Congruence
Welcome to NCTB Solution. Here with this post we are going to help 7th class students for the Solutions of Rd Sharma Class 7 Mathematics, Chapter 16, Congruence. Here students can easily find Exercise wise solution for chapter 16, Congruence. Students will find proper solutions for Exercise 16.1, 16.2, 16.3, 16.4 and 16.5. Our teachers solved every problem with easily understandable methods so that every students can understand easily. Here all solutions are based on the CBSE latest curriculum.
Congruence Exercise 16.1 Solution
Question no – (1)
Solution :
Congruent : The word congruent means same shape and size, that is equal in every respect. Thus if two figure have exactly the same shape and size they are said to be congruent.
Question no – (2)
Solution :
(i) Two line segments are congruent if ‘they are of equal lengths’.
(ii) Two angles are congruent if ‘they measures are equal’.
(iii) Two squares are congruent if ‘the same side length’.
(iv) Two rectangles are congruent if ‘the dimensions are same’.
(v) Two circles are congruent if ‘they have Same radius’.
Question no – (3)
Solution :
Yes, we can say that ∠POR ≅ ∠QOS
Question no – (4)
Solution :
Angle which is congruent to ∠AOC is,
∠AOC is congruent to ∠DOB
Question no – (6)
Solution :
∠AOB is congruent to ∠FYQ.
Question no – (7)
Solution :
(i) All squares are congruent – (False).
(ii) If two squares have equal areas, they are congruent – (True).
(iii) If two rectangles have equal area, they are congruent – (False).
(iv) If two triangles are equal in area, they are congruent – (False).
Congruence Exercise 16.2 Solution
Question no – (1)
Solution :
Figure – (i)
Since in △ABC and △DEF
AB = DE, BC = EF and AC = DF
Thus, △ABC ≅ DEF
Figure – (ii)
In triangle △ABC and △ ABD
AD = AC and BC = BD
Hence, △ABC ≅ △ ABD
Figure – (iii)
In △ABD and △CEF
AB = EF and AD = CF
Therefore, △ABC ≅ △CEF
Figure – (iv)
In △ABO and △COD
AB = CD, AO = OC and BO = OD
So, △ABO ≅ △COD
Question no – (2)
Solution :
(i) Is △ABD ≅ △ CBD?
Since AD = DC
and AB = BC
So, △ ABD ≅ △ BDC.
(ii) The three pairs are,
AD = CP, BD = BD and AB = BC
Question no – (3)
Solution :
(i) Is △ ABC ≅ △CDA?
AB = DC
and BC = AD
Therefore, △ABC ≅ △CDA
(ii) What congruence condition have you used?
AB = DC,
BC = AD
and AC = AC
(iii) You have used some fact, not given in the question, what is that?
= AC = CA
Question no – (4)
Solution :
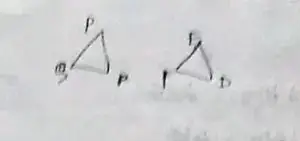
(i) Which side of △ POQ equals ED
= ED = PR
(ii) Which angle of △ POQ equals ∠E
= ∠ED = ∠QPR
Question no – (5)
Solution :
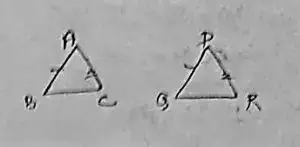
In △ ABC and △PR
FB = AC and PQ = PR
AB = PQ and BC = QR
Yes, △ ABC ≅ △ PQR
Question no – (6)
Solution :
AB = BD,
AC = DC
BC = BC
Therefore, △ABC ≅ △DBC
Question no – (8)
Solution :
As per the question,
△ADB and △ADC
∴ AB = AC
AD = AD
and BD = DC
Since, D is the mid-point of BC
Thus, △ ADB ≅ △ ADC
Question no – (9)
Solution :
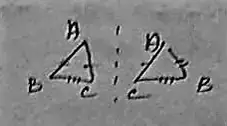
In △ABC and △ACB
AB = AC
BC = CB
AC = AB
Therefore, △ABC ≅ △ACB
Congruence Exercise 16.3 Solution
Question no – (1)
Solution :
Figure – (i)
△AOB ≅ △DOC
Figure – (ii)
△ADC ≅ △APB
Figure – (iii)
△ABD ≅ △BDC
Figure – (iv)
△ABC ≅ △PQR
Question no – (2)
Solution :
Figure – (i)
AB = AD
BC = CD
AC = AC
∴ SSS
Figure – (ii)
AC = BD
AD = BC
AB = AB
∴ SSS
Figure – (iii)
AD = AB
∠AC = ∠AB
AC = AC
∴ SAS
Figure – (iv)
AC = AC
∠DAC = ∠ACB
AD = BC
∴ SAS
Question no – (3)
Solution :
According to the question,
AO = BO
CO = DO
∠AOC = ∠BOD
△AOC ≅ △BOD
Therefore, (ii) △AOC ≅ △BOD
The three pairs of matching parts are,
AO,BO; CO, DO; ∠AOC, ∠BOD
Question no – (5)
Solution :
In the figure,
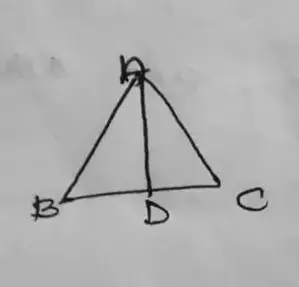
AB = AC
AD = AC
and ∠BAD = ∠CAD
Hence, △ABD ≅ △ADC
Question no – (6)
Solution :
(i) So, △ABC ≅ △ADC
(ii) (a) ∠ABC = ∠ADC
(b) ∠ACD = ∠ACB
(c) Line segment AC bisects ∠BAC and ∠BCD
Question no – (7)
Solution :
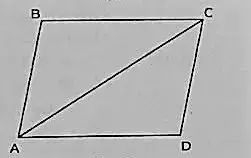
(i) In triangles △ACD and △CAB
∠BCA = ∠CAD
AC = AC
DC = AB
Thus, △ACD ≅ △CAB
(ii) The three pairs of matching parts,
AC, CA; DC, BA; ∠DCA, ∠BAC.
(iii) ∠CAD is equal to ∠ACB
(iv) Yes since ∠BAC = ∠ACD
Congruence Exercise 16.4 Solution
Question no – (1)
Solution :
Figure – (i)
In △ABD and △CDO
∠B = ∠D
∠BOA = ∠COD
AB = DC
So, △ABD ≅ △CDO
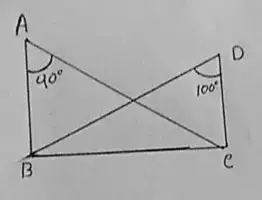
Figure – (ii)
∠C = 180 – (50 – 90)
= 40
∴ In triangle ABD and ADC
∠B = ∠C
AD = AC
AB = AC
So, △ABD ≅ △ADC`
Figure – (iii)
∠D = 180 – (90 + 60)
= 30
∠C = 180 – 90 – 30
= 60
∴ ∠A = ∠ D
AC = PR
∠C = ∠ R
∴ △ABC ≅ △PQR
Question no – (2)
Solution :
In given triangle ABD and ADC
AD = AD
BD = D
Since D ids midpoint BC
∠BAD = ∠DAC
Therefore, △ADB ≅ △ADC
(ii) Matching parts are,
∠ABC, ∠ACB; ∠ACB, ∠ABC; BC, CD
(ii) Yes BD = DC since AD ⊥ BC
Question no – (3)
Solution :

∠A = ∠R
AC = PR
∠C = ∠P
Question no – (4)
Solution :
(i) ∠B = ∠C
∴ AB = AC
AC = AB
Therefore, △ABC ≅ △ACB
(ii) Matching parts are,
∠ABC, ∠ACB; ∠ACB,∠ABC; BC,CD
(iii) Yes, it is true.
Question no – (5)
Solution :
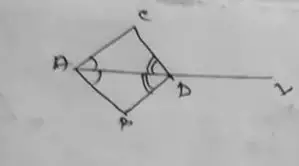
In triangle,
ACD and ABD
∠CAD = ∠BAD
AD = AD
and ∠ACD ≅ △ABD
Therefore, △ACD ≅ △ABD
Question no – (6)
Solution :
(i) Yes, △AOC ≅ △BOD
(ii) Matching pair,
AO = OB
∠A = ∠B
∠AOC = ∠BOD
(iii) Yes, it is true.
Congruence Exercise 16.5 Solution
Question no – (1)
Solution :
Figure – (i)
△ABD ≅ △ABC
Figure – (ii)
△ABD ≅ △ACD
Figure – (iii)
△AOB ≅ △DOC
Figure – (iv)
△ABC ≅ △ADC
Figure – (v)
△ABD ≅ △CBD
Question no – (2)
Solution :
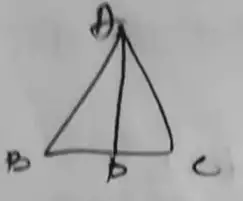
(i) Yes, △ABD ≅ △ACD
(ii) AB = AC
AD = AD
∠ADB = ∠ADC
(iii) Yes, it is true since AD ⊥ BC
Question no – (3)
Solution :
Yes, △ABD ≅ △ACD
BD is equal to CD
In △ADC ∠B = ∠C
Question no – (5)
Solution :
(i) Yes, △BCD ≅ △CBE
(ii) DD = CE
CB = CB
∠D = ∠E
Therefore, △BCD ≅ △CBE
Next Chapter Solution :
👉 Chapter 18 👈