Rd Sharma Solutions Class 6 Chapter 2 Playing With Numbers
Welcome to NCTB Solution. Here with this post we are going to help 6th class students for the Solutions of Rd Sharma Class 6 Mathematics, Chapter 2, Playing With Numbers. Here students can easily find Exercise wise solution for chapter 2, Playing With Numbers. Students will find proper solutions for Exercise 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 2.10 and 2.11. Our teachers solved every problem with easily understandable methods so that every students can understand easily. Here all solutions are based on the CBSE latest curriculum.
Playing With Numbers Exercise 2.1 Solution
Question no – (1)
Solution :
(i) A factor of a number is an exact division of that number.
(ii) A multiple of a number is a number obtained by multiplying it by a natural number.
Question no – (2)
Solution :
(i) 60
Factor of 60 are,
= 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
(ii) 76
Factors of 76 are,
= 1, 2, 3, 4, 19, 38, 76
(iii) 125
Factors of 125 are,
= 1, 5, 25, 125
(iv) 729
Factors of 729 are,
= 1, 3, 9, 27, 81, 243, 729
Question no – (3)
Solution :
(i) 25
∴ First 5 multiple of 25 are
= 25, 50, 75, 100, 125
(ii) 35
∴ First 5 multiple 35 are
= 35, 70, 105, 140, 175
(iii) 45
∴ First 5 multiple of 45 are
= 45, 90, 135, 180, 225
(iv) 40
∴ First 5 multiple of 40 are,
= 40, 80, 120, 160, 200
Question no – (4)
Solution :
15625 is the number have 15 as their factor.
Therefore, correct option is – (ii) 15625
Question no – (5)
Solution :
(i) 21063
= 2 + 1 + 0 + 6 + 3
= 12 ÷ 3
= 4
And, 63 ÷ 7
= 9
So, 21063 is divisible by 21
(ii) 20163
= 2 + 0 + 1 + 6 + 3
= 12 divisible by 3
Now, 2016 – (2 × 3)
= 2016 – 6
= 2010 is not multiple of 7
Therefore, it is not divisible by 21.
So, the correct option is – (ii) 20163.
Question no – (6)
Solution :
(i) 1111
Sum of digit of odd places
= 1 + 1
= 2
Sum of digit of e places
= 1 + 1
= 2
∴ Difference
= (2 – 2)
= 0
Therefore, 1111 is divisible by 11.
(ii) 11011
Sum of digits of odd places
= 1 + 0 + 1
= 2
Sum of digits of even place
= 1 + 1
= 2
∴ Difference
= (2 – 2)
= 0
Therefore, It is divisible by 11
(iii) 110011
Sum of digits of odd places
= 1 + 0 + 1
= 2
Sum of digits of even places
= 1 + 0 + 1
= 2
∴ Difference
= (2 – 2)
= 0
Therefore, 110011 is divisible by 11.
Question no – (7)
Solution :
(i) 55
Here the unit digit is 5,
Hence, 55 is divisible by 5.
(ii) 555
Here, the unit digit is 5
Thus, 555 is divisible by 5.
(iii) 5555
Here, the unit digit 5
So, it is divisible by 5.
(iv) 50005
Unit digit is 5
Therefore, it is divisible by 5.
Question no – (9)
Solution :
Between 1 to 100, there has exactly three factors are,
4, 9, 25, 49
Because 4 = 1, 2, 4
9 = 1, 3, 9
25 = 1, 5, 25
49 = 1, 7, 49
Question no – (10)
Solution :
The numbers which are divisible by 2 are even and which are not divisible by 2 ; odd numbers
Therefore, 42, 144 are even and 89, 321 89 are odd numbers.
Playing With Numbers Exercise 2.2 Solution
Question no – (1)
Solution :
(i) 15 and 25
15 = 1 × 15
= 3 × 5;
25 = 1 × 25
= 5 × 5
∴ Factors of 15 are = 1, 3, 5, 15
∴ Factors of 25 are = 1, 5, 25
Therefore, Common factors are 1, 8, 5
(ii) 35 and 50
35 = 1 × 35
= 5 × 7
50 = 1 × 50
= 2 × 25
= 5 × 10
Therefore, Common factors are 1 and 5
(iii) 20 and 28
20 = 1 × 20
= 2 × 10
= 4 × 5
28 = 1 × 28
= 2 × 14
= 4 × 7
Therefore, Common factors are 1, 2, 4
Question no – (2)
Solution :
(i) Given, 5, 15 and 25
Here, factors of 5 are 5
= 1 × 5 (1, 5)
Factor of 15 = 1 × 15
= 3 × 5
Are (1, 3, 5, 15)
Factor of 25 = 1 × 25
= 5 × 5
Are, (1, 5, 25)
Therefore, Common factors are (1 and 5)
(ii) Given 2, 6 and 8
Here, Factors of 2 = 1 × 2
Factors of 6 = 1 × 6
= 2 × 3
Factors of 8 = 1 × 8
= 2 × 4
Therefore, Common factors of 2, 6, 8 are 1 and 2
Question no – (3)
Solution :
Multiples of 6 are,
= 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78
Factors of 8 are,
= 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96………..
Therefore, First three common multiples are 24, 48, 72.
Question no – (4)
Solution :
Multiples of 12 are,
12, 24, 36, 46, 60, 72, 84, 96, 108, 120
Multiples of 18 are,
= 18, 36, 54, 72, 90, 108, 126………….
Hence, First two common multiples are 36, 72.
Question no – (5)
Solution :
Here, Factors of 7 = 1 × 7 (1, 7)
Factor of 17 = 1 × 16
= 2 × 8
= 4 × 4
Factor are (1, 2, 4, 8, 16)
Thus, the Common Factor of 7 and 16 is 1 and the number is divisible by 1
Question no – (6)
Solution :
Factors of 24 are 24 = 1 × 24
= 2 × 12
= 3 × 8
= 4 × 6
24 factors are 1, 2, 3, 4, 6, 8, 12, 24
∴ The number is divisible by 1, 2, 3, 4, 6, 8, and 12.
Playing With Numbers Exercise 2.3 Solution
Question no – (1)
Solution :
A number is called a prime number it it has no factor other than 1 and the number itself.
∴ Between 1 to 30 prime number are,
= 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Question no – (2)
Solution :
(i) 10 and 50
The prime numbers between 10 and 50 are,
= 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47
(ii) 70 and 90
Prime numbers between 70 and 90 are,
= 71, 73, 79, 83, 89
(iii) 40 and 85
Prime numbers between 40 and 85 are,
= 41, 43, 47, 53, 59, 61, 67, 71, 79, 83
(iv) 60 and 100
Prime numbers between 60 and 100 are,
= 61, 67, 71, 73, 79, 83, 97
Question no – (3)
Solution :
2 is smallest prime number,
Yes, it is an even number.
Question no – (4)
Solution :
3 is the smallest odd prime number
No, every odd numbers is not a prime number
Example – 9 is an odd number having factors 1, 3, and is not a prime.
Question no – (5)
Solution :
A number is called a composite number if it has at least one factor other than 1 and number itself.
Example – 4, 6, 8, etc.
Yes, a composite number can be odd.
‘9’ is the smallest odd composite number.
Question no – (6)
Solution :
Two prime numbers are known as twin primes if there is only one composite number between them.
Example – (3, 5), (5, 7), (11, 13)
Between 50 to 100 twin primes are,
= (59, 61) (71, 73)
Question no – (7)
Solution :
Two numbers are said to be co-prime if they do not have a common factor. Other than 1.
Five pairs of co-prime are,
= (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)
Question no – (8)
Solution :
(i) Two prime numbers are always co-prime to each other
Example : – 7 and 11
(ii) One prime and composite number are not always co-prime
Example : – 3 and 21 not co-prime
(iii) Two composite numbers are always co-prime to each other.
Question no – (9)
Solution :
(i) 13
= 3 + 3 + 7
(All prime numbers)
(ii) 130
= 59 + 71
(All prime numbers)
(iii) 180
= 101 + 79
(All prime numbers)
Question no – (10)
Solution :
(i) 36
= 29 + 7
(Sum of odd prime numbers)
(ii) 42
= 5 + 37
(Sum of odd prime numbers)
(iii) 84
= 17 + 67
(Sum of odd prime numbers)
Question no – (11)
Solution :
(i) 31
∴ Odd prime numbers,
= 5 + 7 + 19
= 31
(Sum of odd prime numbers)
(ii) 35
∴ Odd prime numbers,
= 5 + 7 + 23
= 35
(Sum of odd prime numbers)
(iii) 49
∴ Odd prime numbers,
= 3 + 5 + 41
= 49
(Sum of odd prime numbers)
Question no – (12)
Solution :
(i) 36
Now, Sum of twin primes,
= 17 + 19
= 36
(ii) 84
Now, Sum of twin primes,
= 41 + 42
= 84
(iii) 120
Now, Sum of twin primes,
= 59 + 61
= 120
Question no – (13)
Solution :
(i) 29
Possible missing twins are,
= 31 and 27
(ii) 89
= 87 and 91 possible
∴ Both numbers are not prime
89 has no twin
(iii) 101
= Possible missing twins 99 and 103
∴ 99 is not prime
So, 103 is the missing twin.
Question no – (14)
Solution :
(i) Two number are said to be co-prime if they do not have a common factor other than 1
Here, all numbers are co-prime.
(ii) A number is called a prime number if it has no factor other 1 and no itself
Example :- (59, 61), 71, 73.
(iii) A numbers is called composite number if it has at least one factor other than 1 and the number itself .
Example :- 55, 57; 63, 65.
Question no – (15)
Solution :
The possible digit in the units place to be prime can be 1, 3, 7 or 9.
Example :- 11, 13, 17, 19 etc.
Question no – (16)
Solution :
Seven consecutive composite numbers less than 100,
The required numbers are,
= 90, 91, 92, 93, 95, 96
Question no – (17)
Solution :
(i) Given statement is False.
(ii) Given statement is True.
(iii) Given statement is False.
(iv) Given statement is False.
(v) Given statement is False.
(vi) Given statement is False.
(vii) Given statement is True.
Question no – (18)
Solution :
(i) A number having only two factors is called a Prime number.
(ii) A number having more than two factors is called a Composite number.
(iii) 1 is neither prime nor composite.
(iv) The smallest prime number is 2.
(v) The smallest composite number is 4
Playing With Numbers Exercise 2.4 Solution
Question no – (1)
Solution :
In these (ii) 70 = 2 × 5 × 7 is a prime factorization.
Because 2, 5, 7 are prime numbers.
Question no – (2)
Solution :
(i) Given number, 216
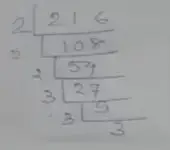
∴ Prime factorization of 216 is
= 2 × 2 × 2 × 3 × 3 × 3
(ii) Given number, 420
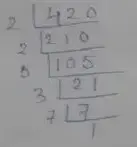
∴ Prime factorization of 420 is
= 2 × 2 × 5 × 3 × 7
(iii) Given number, 468
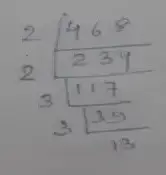
∴ Prime factorization of 468 is
= 2 × 2 × 3 × 3 × 13
(iv) Given number, 945

∴ Prime factorization of 945 is
= 3 × 3 × 3 × 5 × 7
(v) Given number, 7325
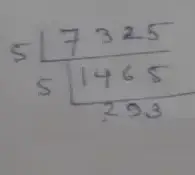
∴ Prime factorization of 7325 is
= 5 × 5 × 293
(vi) Given number, 13915
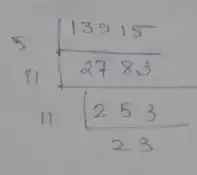
∴ Prime factorization of 13915 is
= 5 × 11 × 11 × 23
Question no – (3)
Solution :
As we know,
Smallest 4 digit number is 1000,
Prime factorization of 1000,
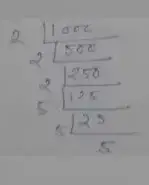
∴ 1000 = 2 × 2 × 2 × 5 × 5 × 5
Question no – (4)
Solution :
As we know,
The largest 4 digit number is 9999
Prime factorization of 9999
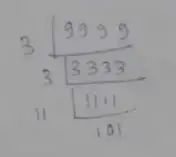
∴ 9999 = 3 × 3 × 11 × 101
Question no – (5)
Solution :
Given number, 1729
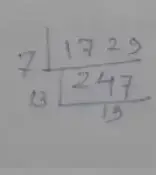
∴ 1729 = 7 × 13 × 19
Each factor is 6 more than the previous factor.
Question no – (6)
Solution :
1 and the no itself are not included in the prime factorization of a composite number.
Example : the number is 4 because 4 = 2 × 2
(Both are prime numbers)
Question no – (7)
Solution :
Missing numbers for Tree (i) are,
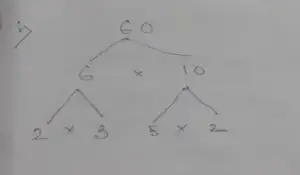
Missing numbers for Tree (ii) are,
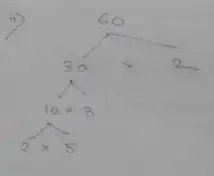
Playing With Numbers Exercise 2.5 Solution
Question no – (1)
Solution :
We know that,
A natural number is divisible by 2 if its unit digit place 0, 2, 4, 6 or 8
Therefore,
(i) 6250 is divisible by 2
(ii) 984325 is not divisible by 2
(iii) 367314 is divisible by 2.
Question no – (2)
Solution :
As we know that,
A number is divisible by 3 if the sum of digits is divisible by 3.
(i) 70335
= 7 + 0 + 3 + 3 + 5
= 18 ÷ 3
= 6
∴ It is divisible by 3
(ii) 607439
= 6 + 0 + 7 + 4 + 3 + 9
= 29 ÷ 3
= 6
∴ It is not divisible by 3
(iii) 9082746
= 9 + 0 + 8 + 2 + 7 + 4 + 6
= 36 ÷ 3
= 12
∴ It is divisible by 3
Question no – (3)
Solution :
As we know that,
A number is divisible by 6 if it is divisible by 2 and 3.
(i) 7020
= 7020 – Unit digit 0 so it divisible by 2
= 7 + 0 + 2 + 0 = 9 ÷ 3 = 3
So, it is divisible by 3
(ii) 56423
Here, the unit digit 3 so it not divisible by 2
and, 5 + 6 + 4 + 2 + 3 = 20 it is not divisible by 3
So, it is not divisible by 6
(iii) 732510
Here, unit digit is ‘0’ so it divisible by 2,
and, 7 + 3 + 2 + 5 + 1 + 0 = 18 ÷ 3 = 6
So, it is divisible by 6
Question no – (4)
Solution :
We know that,
A number is divisible by 4 if the last two digit of the number is divisible by 4
So, the number is divisible by 4,
(i) 786532
= 32 ÷ 4 = 8
Hence, it is divisible by 4
(ii) 1020531
= 31 ÷ 4 = not divisible
Hence, is not divisible by 4.
(iii) 9801523
= 23 ÷ 4 = not divisible
Hence, it is not divisible by 4
Question no – (5)
Solution :
As we know that,
A number is divisible by 8 it the last three digits of the number is divisible by 8.
(i) 8364
= 364 ÷ 8 is not divisible
∴ It is not divisible by 8
(ii) 7314
= 314 is not divisible by 800
∴ The number is not divisible by 8,
(iii) 36712
= 712 is divisible by 8
So, 36712 is divisible by 8.
Question no – (6)
Solution :
We know that,
A number divisible by 9 if the sum of the digits is divisible by 9.
(i) 187245
= 1 + 8 + 7 + 2 + 4 + 5 = 27 is divisible.
So, 187245 is divisible by 9
(ii) 3478
= 3+ 4 + + 7 + 8 = 22 is not divisible by 9
So, 3478 is not divisible
(iii) 547218
= 54218 = 5 + 4 + 7 + 2 + 1 + 8 = 27 is divisible by, 9
So, 547218 is divisible by 9.
Question no – (7)
Solution :
As we know that,
A number is divisible by 11 if the sum of odd place and the sum of even place. And then their difference is divisible by 11.
(i) 5335
= Sum of digits at even place
3 + 5 = 8 ‘
Sum of odd place digit = 5 + 3 = 8
∴ (8 – 8) = 0
∴ 5335 is divisible by 11
(ii) 70169803
= Sum of digits of odd place
= 7 + 1 + 9 + 0 = 17
Sum of digits even place = 0 + 6 + 8 + 3 = 17
∴ (17 – 17) = 0
(iii) 10000001
= Sum of digits at even place
0 + 0 + 0 + 1 = 1
Sum of odd place digit
= 1 + 0 + 0 + 0 = 1
∴ (1 – 1 ) = 0
∴ 10000001 is divisible by 11.
Question no – (8)
Solution :
(i) 75 * 5
= 7 + 5 + 5
= 17 + 1
= 18 ÷ 3 = 6
∴ So, 7515 this no divisible by 3.
(ii) 35 * 64
= 3 + 5+ 6 + 4
=18 + 3
= 21 ÷ 3 = 7 ‘
∴ 25 364 is divisible by 3
(iii) 18 * 71
= 1 + 8 + 7 + 1
= 17 + 1
= 18 ÷ 3 = 6
∴ The number is 18171
Question no – (11)
Solution :
(i) 2 but not by 4.
= The number is 10.
(ii) 3 but not by 6.
= The number is 15
(iii) 4 but not by 8.
= The number is 28.
(iv) both 4 and 8 but not by 32.
= The number is 48
Question no – (12)
Solution :
(i) Given statement is False.
(ii) Given statement is True.
(iii) Given statement is False.
(iv) Given statement is True.
(v) Given statement is False.
(vi) Given statement is True.
(vii) Given statement is False.
(viii) Given statement is True.
(ix) Given statement is False.
(x) Given statement is True.
Playing With Numbers Exercise 2.6 Solution
Question no – (1)
Solution :
(i) Given number, 144, 198
Prime factorization of 144,
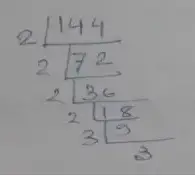
∴ 144 = 2 × 2 × 2 × 2 × 3 × 3× 13
Prime factorization of 198,
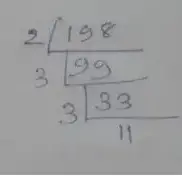
∴ 198 = 2 × 3 × 3 × 11
∴ H.C.F is = 2 × 3 × 3 = 18
So, HCF of 144 and 198 is 18
(ii) Given number, 81.117
Prime factorization of 81,
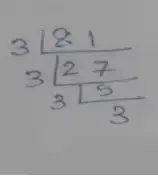
∴ 81 = 3 × 3 × 3 × 3
Prime factorization of 117,
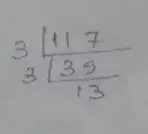
∴ 117 = 3 × 3 × 13
∴ H.C.F is = 2 × 7 = 14
So, HCF of 81 and 117 is 14.
(iii) Given number, 84, 98
Prime factorization of 84,
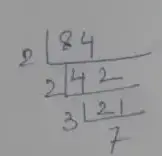
∴ 84 = 2 × 2 × 3 × 7
Prime factorization of 98,
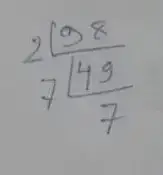
∴ 98 = 2 × 7 × 7
∴ H.C.F is = 2 × 7 = 14
So, HCF of 84 and 98 is 14.
(iv) Given number, 225, 450
Prime factorization of 225,

∴ 225 = 5 × 5 × 3 × 3
Prime factorization of 450,
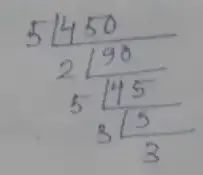
∴ 450 = 5 × 2 × 5 × 3 ×
∴ H.C.F is = 5 × 5 × 3 × 3 = 225
So, HCF of 225 and 450 is 225.
(v) Given number, 170, 238
Prime factorization of 170,
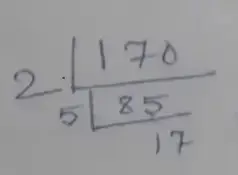
∴ 170 = 2 × 5 × 17
Prime factorization of 238,
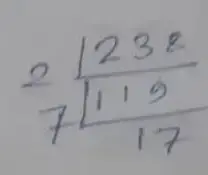
∴ 238 = 2 × 7 × 17
∴ H.C.F is = 2 × 17 = 34
So, HCF of 170 and 238 is 34.
(vi) Given number, 504, 980
Prime factorization of 504,

∴ 504 = 2 × 2 × 2 × 2 × 3 × 3 × 7
Prime factorization of 980,

∴ 980 = 2 × 7 × 7 × 2 × 5
∴ H.C.F is = 2 × 2 × 7 = 28
So, HCF of 504 and 980 is 28
(vii) Given number, 150, 140, 210
Prime factorization of 150,

∴ 150 = 2 × 5 × 5 × 3
Prime factorization of 140,
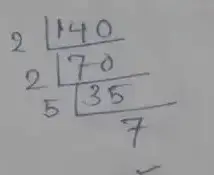
∴ 140 = 2 × 2 × 5 × 7
Prime factorization of 210,

∴ 210 = 3 × 2 × 5 × 7
∴ H.C.F is = 2 × 5 = 10
Therefore, HCF of 150, 140 and 210 is 10.
(viii) Given number, 84, 120, 138
Prime factorization of 84,
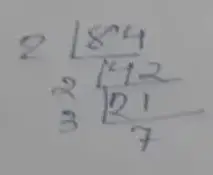
∴ 84 = 2 × 2 × 3 × 7
Prime factorization of 120,
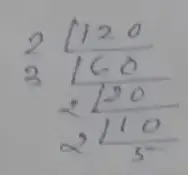
∴ 120 = 2 × 3 × 2 × 2 × 5
Prime factorization of 138,
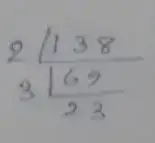
∴ 138 = 2 × 3 × 23
∴ H.C.F is = (2 × 3) = 6
So, HCF of 84, 120 and 138 is 6.
Question no – (2)
Solution :
HCF of two consecutive numbers is 1.
HCF of two consecutive Even numbers is 2.
HCF of two consecutive Odd numbers is 1.
Question no – (3)
Solution :
Here, 4 = 2 × 2 and 15 = 3 × 5
No, it is wrong the H.C.F of two co-prime numbers is 1. 4and 15 are co-prime numbers heavy common faction 1?
Playing With Numbers Exercise 2.7 Solution
Question no – (1)
Solution :
(i) Given, 300, 450

∴ H.C.F of 300, 450 is 150
(ii) Given, 399, 437
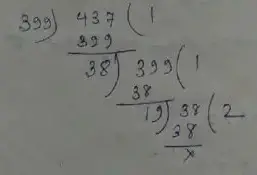
∴ H.C.F of 399, 437 is 19
(iii) Given, 1045, 1520
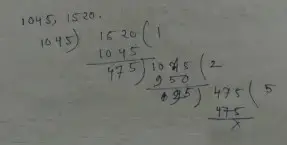
∴ H.C.F of 1045, 1520 is 95
Question no – (2)
Solution :
(i) Given pair, 59, 97
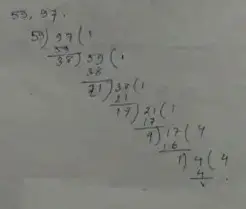
Here, the last divisor is 1.
Therefore, the number 59, 97 are co-prime.
(ii) Given numbers, 875, 1859
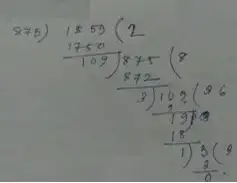
∴ Last divisor is 1.
Therefore, the numbers 875 and 1859 are co-prime.
(iii) Given, 288, 1375

Here, the last divisor is 1.
∴ The numbers 288 and 1375 are co-prime.
Question no – (3)
Solution :
HCF of two consecutive numbers is 1.
Because there is no common factor between two consecutive numbers.
Question no – (4)
Solution :
(i) Given statement is True.
(ii) Given statement is True.
(iii) Given statement is False.
(iv) Given statement is True.
(v) Given statement is False.
Playing With Numbers Exercise 2.8 Solution
Question no – (1)
Solution :
Here, (615 – 6) = 609
and (963 – 6) = 957
So, now,
609 = 3 × 7 × 29
957 = 3 × 11 × 29
∴ H.C.F is = (3 × 29) = 87
Therefore, the required number is 87.
Question no – (2)
Solution :
Here, (285 – 9) 276
And (1249 – 7) = 1242
∴ Now,
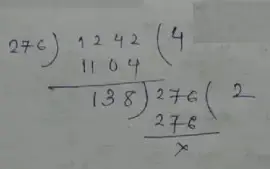
∴ H.C.F is = 138
Therefore, the required number is 138.
Question no – (3)
Solution :
Here,
(626 – 1) 625 (3127 – 2) = 3125
And, (15628 – 3) = 15625
∴ Now,
625 = 5 × 5 × 5 × 5
3125 = 5 × 5 × 5 × 5 × 5
15625 = 5 × 5 × 5 × 5 × 5 × 5
∴ H.C.F is = (5 × 5 × 5 × 5) = 625
Therefore, the required number is 625.
Question no – (4)
Solution :
In the question,
Room, Length = 8m 25 cm = 825 cm
breadth = 6 m 75 cm = 657 cm
Height = 4 cm 50 cm = 450
∴ Now,
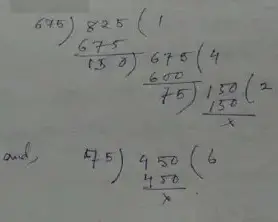
Therefore, the length of the required rod is 75 cm.
Question no – (5)
Solution :
Given Courtyard,
length = 2016 cm.
breadth = 1560 cm.
Now,
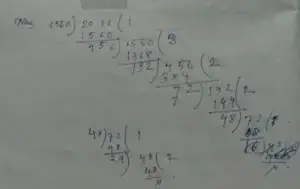
∴ H.C.F is = 24
Therefore, least possible number of stones is 24.
Question no – (6)
Solution :
Here,
length of tapes are 7 m, 3m 85 cm, 12 m 95 cm
= 700 m, 385 cm, 1295 cm,
Now, the Factors of,
= 700 = 2 × 2 × 5 × 7 × 5
= 385 = 5 × 11 × 7
= 1295 = 5 × 7 × 37
∴ The H.C.F is,
= (5 × 7)
= 35
Therefore, the length of longest tape will be 35 cm.
Question no – (7)
Solution :
Acceding to the question,
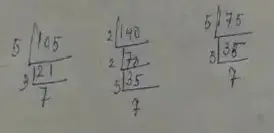
∴ 105 = 5 × 3 × 7
∴ 140 = 2 × 2 × 5 × 7
∴ 175 = 5 × 5 × 7
∴ H.C.F is = (5 × 7) = 35
Hence, 35 animals went in each thief.
Question no – (8)
Solution :
According to the question,
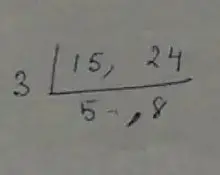
∴ L.C.M is = 3 × 5 × 8 = 120
∴ 120 chocolates should be purchased.
∴ No of boxes of A should be purchased,
= 120 ÷ 24
= 5
∴ No of boxes of B should be purchased,
= 120 ÷ 15
= 8
Question no – (9)
Solution :
According to the question,
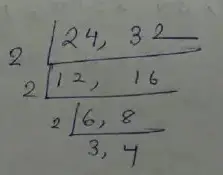
∴ L.C.M is = 2 × 2 × 2 × 3 × 4
= 96
∴ 96 pencils each bought.
∴ 96 ÷ 24 = 4 pack of color pencils
∴ 96 ÷ 32 = 3 pack of crayons.
Question no – (10)
Solution :
(i) 161/207
= 161/207
= 161 ÷ 23/207 ÷ 23
= 7/9
For more better understand :
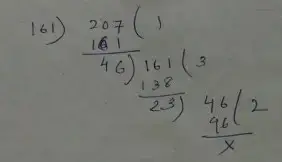
(ii) 296/481
= 296/481
= 296 ÷ 37/481 ÷ 37
= 8/13
For more better understand :
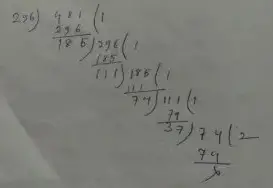
Playing With Numbers Exercise 2.9 Solution
Question no – (1)
Solution :
(i) Given numbers, 48 and 60
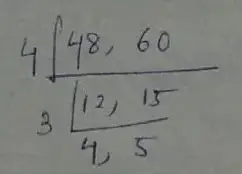
∴ L.C.M is,
= 4 × 3 × 4 × 5
= 240
Thus, the LCM of 48 and 60 is 240.
(ii) Given number, 42, 63
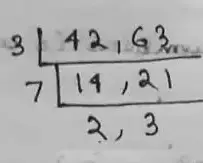
∴ L.C.M is,
= 3 × 7 × 2 × 3
= 126
Therefore, the LCM of 42 and 63 is 126.
(iii) Given number, 18 and 17
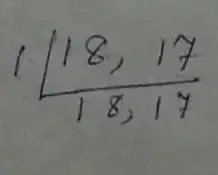
∴ L.C.M is,
= 18 × 17
= 306
Thus, the L.C.M. of 18 and 17 is 306.
(iv) Given number, 15, 30 and 90

∴ L.C.M is,
= 3 × 5 × 2 × 3 × 1
= 90
Thus, the L.C.M of 15, 30 and 90 is 90.
(v) Given numbers, 56, 65 and 85
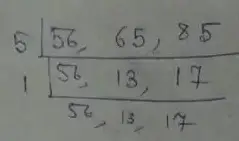
∴ L.C.M is
= 5 × 56 × 13 × 17
= 61880
Hence, the LCM of 56, 65 and 85 is 61880.
(vi) Given numbers, 180, 384, 144
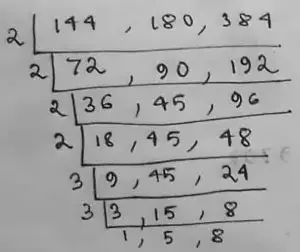
∴ L.C.M is,
= 2 × 2 × 2 × 2 × 3 × 3 × 5 × 8
= 5760
Hence, L.C.M of 144, 180 and 384 is 5760.
(vii) Given numbers, 108, 135, 162
Now,

∴ LCM is
= 2 × 2 × 3 × 3 × 5 × 9
= 1620
Thus, the LCM of 108, 135, and 162 is 1620.
(viii) Given numbers, 28, 36, 45, 60

∴ LCM is,
= 2 × 2 × 3 × 3 × 5 × 7
= 1260
Hence, the LCM is 28, 36, 45, 60 is 1260.
Playing With Numbers Exercise 2.10 Solution
Question no – (1)
Solution :
According to the question,

∴ L.C.M is = 6 × 2 × 3 × 2 × 3
= 216
∴ The required number is 216
Now,
Required smallest number is,
= (216 +5)
= 221
Therefore, the smallest number is 221.
Question no – (2)
Solution :
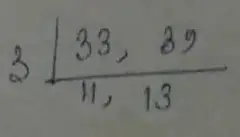
∴ L.C.M is,
= 8 × 11 × 13
= 429
∴ Required smallest no is,
= 429 + 56
= 434
Thus, the smallest number is 434.
Question no – (4)
Solution :
According to question,
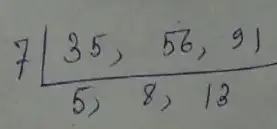
∴ L.C.M is,
= (7 × 5 × 8 × 13)
= 3640
∴ Required smallest no is,
= (3640 + 7)
= 3647
Thus, the smallest number is 3647
Question no – (5)
Solution :
According to question,
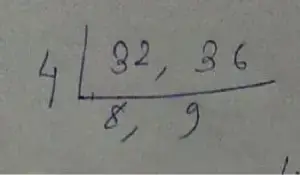
∴ L.C.M is
= (4 × 8 × 9)
= 288 books
Therefore, the minimum 288 books required.
Question no – (6)
Solution :
According to question,

∴ L.C.M is
= 5 × 2 × 8 × 17 × 9
= 12240 cm
= 122 m 40 cm
Therefore, the minimum distance each should walk is 122 m 40 cm.
Question no – (7)
Solution :
According to the question,

∴ L.C.M is,
= 3 × 5 × 8 × 7
= 840
Now,
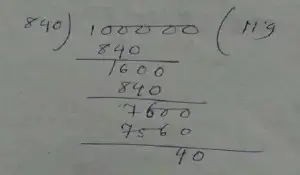
∴ The required no is,
= 100000 + (840 – 40)
= 100000 + 800
= 100800
Therefore, the required number is 100800.
Question no – (8)
Solution :
According to the question,
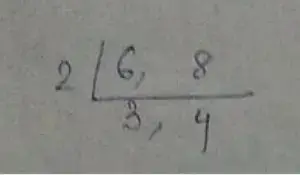
∴ L.C.M is,
= (2 × 3 × 4)
= 24
= 24th block.
So, at 24th block bus stop both of them will stop.
Question no – (9)
Solution :
According to the question,
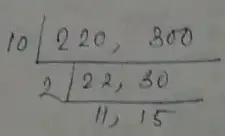
∴ L.C.M is
= 10 × 2 × 11 × 15
= 3300
Therefore, the next heap which lies at the foot of a pole is 3300 m.
Question no – (10)
Solution :
According to the question,

∴ L.C.M is
= (4 × 7 × 8)
= 224
∴ (28 – 8) = 20
And (32 – 12) = 20
∴ Required no is,
= (224 – 20)
= 204
Therefore, the smallest number is 204.
Playing With Numbers Exercise 2.11 Solution
Question no – (1)
Solution :
(i) Given numbers, 25, 65

∴ L.C.M is = (5 × 5 × 13) = 325
∴ H.C.F is = 5
∴ product of numbers = 25
∴ H.C.F × L.C.M
= (5 × 325)
= 1625
(ii) Given numbers, 117, 221
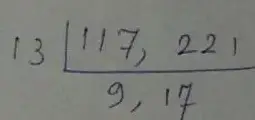
∴ H.C.F is = 13
∴ L.C.M is = 13 × 9 × 17 = 1989
∴ Product of numbers
= (117 × 221)
= 25857
∴ Product of H.C.F and L.C.M
= (13 × 1989)
= 25857
(iii) Given numbers, 35, 40
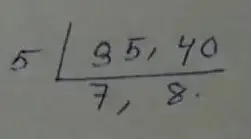
∴ H.C.F is = 5
∴ L.C.M is = (5 × 7 × 8) = 280
∴ Product of numbers
= 35 × 40
= 1400
∴ Product of H.C.F and L.C.M
= 5 × 280
= 2400
Question no – (2)
Solution :
(i) Given numbers, 117, 221

∴ H.C.F is = 13
∴ L.C.M is
= (13 × 9 × 17)
= 1989
Therefore, the HCF is 13 and LCM is 1989.
(ii) Given numbers, 234, 572

∴ L.C.M is
= 2 × 117 × 286
= 5148
Therefore, LCM is 5148.
(iii) Given numbers, 145, 232
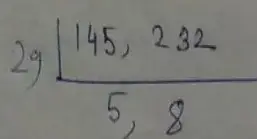
∴ H.C.F is = 29
∴ L.C.M. is
= 29 × 5 × 8
= 1160
Therefore, the HCF is 29 and LCM is 1160.
Question no – (3)
Solution :
In the question,
L.C.M and H.C.F. of two numbers = 180 and 6 respectively
One of the numbers = 30
Other number = ?
∴ Other no is,
= 6 × 180/30
= 36
Therefore, the other number is 36.
Question no – (4)
Solution :
In the given question,
H.C.F. of two numbers is 16 and their product is 3072
L.C.M = ?
∴ L.C.M is
= 3072/16
= 192
Hence, their L.C.M. is 192.
Question no – (5)
Solution :
From the question we get,
H.C.F. of two numbers is 145
L.C.M. is 2175
One number is 725
Other number = ?
∴ The other number is,
= 145 × 2175/725
= 435
Thus, the other number is 435.
Question no – (6)
Solution :
As we know that,
16 does not divide 380.
So, no such numbers can exist with 16 as H.C.F and 380 as L.C.M.
Previous Chapter Solution :
👉 Chapter 1 👈