Warning: Undefined array key "https://nctbsolution.com/ncert-exemplar-solutions-class-6-mathematics/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Ncert exemplar Solutions Class 6 Mathematics Integers
Welcome to NCTB Solutions. Here with this post we are going to help 6th class students for the Solutions of NCERT Class 6 Mathematics Book, Unit 3, Integers. Here students can easily find step by step solutions of all the problems for Integers, Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get Unit 3 solutions.
Integers Unit 3 Solution :
Multiple Choice Questions :
Question no – (1)
Every integer less than 0 has the sign
Solution :
Every integer less than 0 has the Negative (-) sign.
Hence the correct answer is option – (B) –
Question no – (2)
The integer ‘5 units to the right of 0 on the number line’ is
Solution :
On right side of 0 on number line positive integers are there.
On left side of 0 on number line negative integers are there.
‘5 units to the right of 0 on the number line’ = + 5
Thus, correct answer is option (A) +5
Question no – (3)
The predecessor of the integer –1 is
Solution :
The predecessor of any number is the previous number of the given number.
The predecessor of the integer -1 is -2 because -2 is less than -1.
So, the correct answer is option (C) -2
Question no – (4)
Number of integers lying between –1 and 1 is
Solution :
Number of integers lying between –1 and 1 is 0.
Thus, correct answer is option (D) – 0
Question no – (5)
Number of whole numbers lying between –5 and 5 is
Solution :
The number of integers lying between –5 and 5 is -4,-3,-2,-1, 0, 1, 2, 3, 4
Hence, the number of integers lying between –5 and 5 is 9
Question no – (6)
The greatest integer lying between –10 and –15 is
Solution :
The integer lying between –10 and –15 is –11,-12,-13,-14.
-11 is greatest integer lying between –10 and –15.
Therefore,
The correct answer is option (B) –11
Question no – (7)
The least integer lying between –10 and –15 is
Solution :
The integer lying between – 10 and – 15 is -11,-12,-13,-14.
-14 is least integer lying between -10 and -15.
Hence, correct answer is option (D) -14
Question no – (8)
On the number line, the integer 5 is located
Solution :
On right side of 0 on number line positive integers are there.
5 is the positive integer which lies to the right of 0.
Thus, the correct answer is option (B) to the right of 0
Question no – (9)
In which of the following pairs of integers, the first integer is not on the left of the other integer on the number line?
Solution :
Negative integers are at Left side of 0 on number line.
Positive integers are at Right side of 0 on number line.
(–1, 10), (–5, –3), (–6, 0) in all these first integer is on the left of the other integer on the number line.
But in (–3, – 5) in this the first integer is not on the left of the other integer on the number line.
The correct answer is option (B) (–3, –5)
Question no – (10)
The integer with negative sign (–) is always less than
Solution :
The integer with negative sign (–) is always less than Zero (0).
Hence, correct answer is option (A) 0
Question no – (11)
An integer with positive sign (+) is always greater than
Solution :
An integer with positive sign (+) is always greater than Zero (0).
Thus, the correct answer is option (A) 0
Question no – (12)
The successor of the predecessor of –50 is
Solution :
The successor of any number is the next number of that number.
The predecessor of any number is the previous number of that number.
Predecessor of –50 = -51
The successor of the predecessor of –50 i.e.
The successor of -51 is – 50
Thus, correct option – (C) –50
Question no – (13)
The additive inverse of a negative integer
Solution :
Two integers whose sum is zero are called additive inverses of each other.
The additive inverse of a negative integer is always positive.
Hence, correct answer is option (B) is always positive.
Question no – (14)
Amulya and Amar visited two places A and B respectively in Kashmir and recorded the minimum temperatures on a particular day as –4°C at A and –1°C at B. Which of the following statement is true?
Solution :
Amulya and Amar visited two places A and B respectively in Kashmir.
A place temperature = –4°C
B place temperature = –1°C
From above,
A place is cooler than B place.
Therefore, the correct answer is option (A) A is cooler than B
Question no – (15)
When a negative integer is subtracted from another negative integer, the sign of the result
Solution :
When a negative integer is subtracted from another negative integer, the sign of the result depends on the numerical value of the integers
E.g. -4 – (-9)
= -4 + 9 (- x – = +)
= 5
Thus, the correct answer is option (D) Depends on the numerical value of the integers
Question no – (16)
The statement “When an integer is added to itself, the sum is greater than the integer” is
Solution :
“When an integer is added to itself, the sum is greater than the integer” is true only when the integer is positive.
E.g. 4 + 4 = 8
But, When negative integers are there,
-4 + (-4) = -4 -4 = -8 which is less integer.
Hence, correct answer is option – (C) true only when the integer is positive.
Question no – (17)
Which of the following shows the maximum rise in temperature?
Solution :
0°C to 10°C = 10°C rise in temperature.
-4°C to 8°C = 12°C rise in temperature.
-15°C to –8°C = 7°C rise in temperature.
-7°C to 0°C =7°C rise in temperature.
-4°C to 8°C = 12°C rise in temperature. Which has maximum rise in temperature.
Hence, the correct answer is option – (B) -4°C to 8°C
State True Or False :
Question no – (18)
The smallest natural number is zero
Solution :
Natural number means positive integer. It starts from +1
Zero is not a natural number.
Thus, the statement is False.
Question no – (19)
Zero is not an integer as it is neither positive nor negative
Solution :
This statement is (B) False.
Because zero is an integer as it is neither positive nor negative.
Question no – (20)
The sum of all the integers between -5 and -1 is -6
Solution :
The successor of the integer 1 is 0 – This statement is False.
Because the successor of any integer is the next number of that integer.
Hence the successor of the integer 1 is 2.
Question no – (21)
The successor of the integer 1 is 0
Solution :
The successor of the integer 1 is 0 – This statement is False.
Because the successor of any integer is the next number of that integer.
Hence the successor of the integer 1 is 2.
Question no – (22)
Every positive integer is larger than every negative integer
Solution :
Given statement is – True.
In the number every positive integer lies right of the Zero and all negative integer and they are larger than negative integer.
Question no – (23)
The sum of any two negative integers is always greater than both the integers.
Solution :
Because when negative integers are there,
-4 + (-4) = -4 -4 = – 8 which is less integer.
Hence, the sum of any two negative integers is always smaller than both the integers.
Or,
Two negative integer -5, – 2,
Sum of these = (- 5) + ( – 2)
= – 5 – 2
– 7
= ( – 7 ) < ( – 5) and ( – 2)
In the number line the sum of those integer ( – 7) is in the left. That means (- 7) is smaller than (- 5) and (- 2)
Question no – (24)
Every positive integer is larger than every negative integer
Solution :
Because when negative integers are there,
-4 + (-4) = -4 -4 = – 8 which is less integer.
Hence, the sum of any two negative integers is always smaller than both the integers.
Question no – (25)
The sum of any two negative integers is always greater than both the integers
Solution :
Given statement is – True.
Two positive integer = + 2 and + 5
Sum of these integer = (+ 2) + (+ 5)
= 2 + 5
= 7
7 is greater than 5 and 2
Therefore sum of all positive integer lies in the right of the number link of those integer
So, the sum is greater than both the integer.
Question no – (26)
All whole numbers are integers
Solution :
Given statement is True.
Whole number starts from 0 to 1, 2, …. and does not certain only decimal and fractions
Therefore, all whole number are integer.
Question no – (27)
All integers are whole numbers
Solution :
All integers are whole numbers – This statement is False.
All integers are not whole numbers because
Negative integers are not whole numbers.
Question no – (28)
Since 5 > 3, therefore –5 > –3
Solution :
Since 5 > 3, therefore –5 > –3 – This statement is False.
Because,
5 > 3 this is a positive integers.
But in negative integers sign changes.
-ve sign containing large number is smaller and -ve sign containing small number is larger.
–5 < –3
Question no – (29)
Zero is less than every positive integer
Solution :
Given statement is True.
Every positive integer lies in the right of the Zero
Therefore, zero is less than every positive integer.
Question no – (30)
Zero is less than every positive integer
Solution :
Given statement is True.
In the number Zero lies in the right of every negative integer.
Therefore, zero is larger than every negative integer.
Question no – (31)
Zero is neither positive nor negative
Solution :
Given, statement is True.
Zero is a natural number. It is neither negative nor positive.
Question no – (32)
On the number line, an integer on the right of a given integer is always larger than the integer.
Solution :
Given statement is True.
In the number line is in the right of zero. 1 is greater than 0
2 is in the right of the 1
2 is greater than 1
-1 is in the right of -3
∴ An integer on the right of a given integer is always greater than the integer.
Question no – (33)
-2 is to the left of -5 on the number line
Solution :
Given statement is False.
(-2) is in the right of (- 5) in the number line.
Question no – (34)
The smallest integer is 0
Solution :
Given statement is False.
In the number line there are many integer such as -5, -3, -2, -1 smaller than zero.
Therefore 0 is not the smallest integer.
Question no – (35)
6 and -6 are at the same distance from 0 on the number line.
Solution :
Given statement is True.
6 and (- 6) are at same distance from 0 on the number line.
Question no – (36)
The difference between an integer and its additive inverse is always even
Solution :
Given statement is True.
Let, us an integer is 3
Its addition inverse is = – 3
Difference to integer and its additive inverse is,
= 3 (- 3)
= 3 + 3
= 6 (Even)
Let, us another integer = 4
its additive integer = – 4
Difference of integer its additive inverse is,
= 4 – (- 4)
= 4 + 4
= 8 (Even)
Question no – (37)
The sum of an integer and its additive inverse is always zero
Solution :
Given statement is True.
Let, us take an integer = 4
additive inverse of it = – 4
Sum of integer 4 and its additive inverse is,
= 4 + (- 4)
= 0
Question no – (38)
The sum of two negative integers is a positive integer.
Solution :
Given statement is False.
Let, Us take two negative integer -3, -4,
Sum of them,
= (- 3) + (- 4)
= – 3 – 4
= -7 is also a negative.
Question no – (39)
The sum of three different integers can never be zero.
Solution :
Given statement is False.
Let, Us take there integer + 3, – 1, – 2,
Sum of them = 3 + (- 1) + (- 2)
= 3 – 1 – 2
= 3 – 3
= 0
Therefore, sum of there difference integer can be zero.
Fill in the blanks :
Question no – (40)
Solution :
On the number line, –15 is to the Left of zero.
Because the negative integers to the left of 0 on the number line.
Question no – (41)
Solution :
On the number line, 10 is to the Right of zero.
Because all the positive integers lie to the right of 0.
Question no – (42)
Solution :
The additive inverse of 14 is -14
Two integers whose sum is zero are called additive inverses of each other.
They are also called the negatives of each other.
14 + ? = 0
? = 0 – 14
? = – 14
Question no – (43)
Solution :
The additive inverse of –1 is 1.
Two integers whose sum is zero are called additive inverses of each other.
They are also called the negatives of each other.
(-1) + ? = 0
? = 0 – (-1)
? = 1
Question no – (44)
Solution :
The additive inverse of 0 is 0.
Question no – (46)
Solution :
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= (–11) + (–2) + (–1) = -11 -2 -1
= – 14
= (–11) + (–2) + (–1) = -14
Question no – (47)
Solution :
? + (–11) + 111 = 130
? -11 = 130 – 111(when there is 2 equations and = sign between them when shifting any number
its sign changes.)
? – 11 = 19
? = 19 + 11
? = 30
30 + (–11) + 111 = 130
Question no – (48)
Solution :
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
(– 80) + 0 + (– 90) =
= (– 80) + (– 90)
= -80 – 90
= – 170
(–80) + 0 + (–90) = – 170
Question no – (49)
Solution :
(-5454) – 3456 = -8910
Fill in the blanks using <, = or > :
Question no – (50)
Solution :
On a number line, numbers on left side is smaller than numbers on right side.
Negative integers are at Left side of 0 on number line.
Positive integers are at Right side of 0 on number line
First we add (–11) + (–15)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
-11 – 15 = -26
Now we add 11 + 15
11 + 15 = 26
-26 < 26
∴ (–11) + (–15) < 11 + 15
Question no – (51)
Solution :
On a number line, numbers on left side is smaller than numbers on right side.
Negative integers are at Left side of 0 on number line.
Positive integers are at Right side of 0 on number line.
First we add (– 71) + (+ 9)
When numbers having + and – sign and addition is there.
We subtract smaller number from larger number and give larger number sign.
= – 71 + 9
= – 62
Now we add (– 81) + (– 9)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= (– 81) + (– 9)
= – 81 – 9
= – 90
– 62 > – 90
∴ (–71) + (+9) > (–81) + (–9)
Question no – (52)
Solution :
∴ 0 < 1
Question no – (53)
Solution :
∴ –60 < 50
Question no – (54)
Solution :
∴ –10 > –11
Question no – (55)
Solution :
∴ –101 > –102
Question no – (56)
Solution :
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
First we add (–2) + (–5) + (–6)
= -2 -5 -6 = -13
Now, we add (–3) + (–4) + (–6)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= -3 -4 -6
= -13
-13 = -13
∴ (–2) + (–5) + (–6) = (–3) + (–4) + (–6)
Question no – (57)
Solution :
∴ 0 < –2
Question no – (58)
Solution :
On a number line, numbers on left side is smaller than numbers on right side.
Negative integers are at Left side of 0 on number line.
Positive integers are at Right side of 0 on number line.
First we add 1 + 2 + 3
= 1 + 2 + 3 = 6
Now, we add (–1) + (–2) + (–3)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= (– 1) + (– 2) + (– 3)
= -1 – 2 – 3 = – 6
6 > – 6
∴ 1 + 2 + 3 > (– 1) + (– 2) + (– 3)
Question no – (59)
Solution :
| Column I | Column I |
| (i) The additive inverse of + 2 | (b) -2 |
| (ii) The greatest negative integer | (e) – 1 |
| (iii) The smallest positive integer | (d) 1 |
| (iv) The smallest integer greater than every negative integer. | (a) 0 |
| (v) Sum of predecessor and successor of +1 | (c) 2 |
Question no – (60)
Compute each of the following :
Solution :
(a) 30 + (–25) + (–10)
= 30 + (–25) + (–10)
= 30 – 25 – 10
= -5
(b) (–20) + (–5)
= (–20) + (–5)
= -20 – 5
= -25
(c) 70 + (–20) + (–30)
= 70 + (–20) + (–30)
= 70 – 50
= 20
(e) 1 + (–2) + (– 3) + (– 4)
First we add (– 2) + (– 3) + (- 4)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= (– 2) + (– 3) + (- 4)
= – 2 – 3 – 4
= – 9
Now we add 1 + (- 9)
When numbers having + and – sign and addition is there.
We subtract smaller number from larger number and give larger number sign.
=1 + (- 9)
= 1 – 9
= – 8
Therefore, 1 + (– 2) + (– 3) + (– 4) = – 8
(f) 0 + (– 5) + (– 2)
First we add (–5) + (–2)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= (– 5) + (– 2)
= -5 – 2
= – 7
Now we add 0 + (- 7)
= -7
Therefore, 0 + (– 5) + (– 2) = – 7
(g) 0 – (–6) – (+6)
= 30 + (–25) + (–10)
= 30 – 25 – 10
= -5
(h) 0 – 2 – (–2)
First we add (– 2) + (– 3) + (- 4)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= (– 2) + (– 3) + (- 4)
= – 2 – 3 – 4
= – 9
Now we add 1 + (- 9)
When numbers having + and – sign and addition is there.
We subtract smaller number from larger number and give larger number sign.
=1 + (- 9)
= 1 – 9
= – 8
Therefore, 1 + (– 2) + (– 3) + (– 4) = – 8
Question no – (61)
Solution :
(a) 200 m above sea level
We denote the height of a place above sea level by a positive integer
200 m above sea level = + 200 m
(b) 100 m below sea level
We denote depth below the sea level by a negative integer.
100 m below sea level = – 100 m
(c) 10 m above sea level
We denote the height of a place above sea level by a positive integer
10 m above sea level = +10 m
(d) Sea level
Sea level = 0 m
Question no – (62)
Solution :
(a) Opposite of Decrease in size
= Increase in size
(b) Opposite of Failure
= Success
(c) Opposite of Profit of Rs.10
= loss of Rs. 10
(d) Opposite of 1000 A.D.
= 1000 B.C.
(e) opposite of Rise in water level
= Fall in water level
(f) Opposite of 60 km south
= 60 km North
(g) Opposite of 10 m above the danger mark of river Ganga
= 10 m below the danger mark of river Ganga.
(h) Opposite of 20 m below the danger mark of the river Brahmaputra
= 20 m above the danger mark of river Brahmaputra.
(i) Opposite of Winning by a margin of 2000 votes
= Losing by a margin of 2000 votes.
(j) Opposite of Depositing Rs.100 in the Bank account
= Withdrawing Rs 100 from the Bank.
(k) Opposite of 20°C rise in temperature.
= 20°C fall in temperature.
Question no – (63)
Solution :
Temperature of a place at 12:00 noon was +5°C.
Temperature increased by 3°C in first hour.
Temperature of a place at 1:00 noon = + 5°C + 3°C
Temperature of a place at 1:00 noon = + 8°C
Decreased by 1°C in the second hour.
Temperature of a place at 2:00 pm = + 8°C – 1°C
Temperature of a place at 2:00 pm is + 7°C
Or,
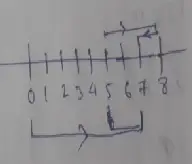
The temperature at 2 : 00 pm is 7°C
Question no – (64)
Solution :
We are arranging numbers 0 to 9 in such way that we get result 3.
(1) 0 – 1 – 2 – 3 – 4 – 5 – 6 + 7 + 8 + 9
= – 21 + 24
= 3
(2) 0 – 1 – 2 – 3 + 4 + 5 – 6 + 7 + 8 – 9
= First we add -1-2-3-6-9
= – 21
Now we add + 4 + 5 + 7 + 8
= 24
= – 21 + 24
= 3
Or,
= 0 – 1 – 2 – 3 – 4 – 6 + 7 + 8 + 9 = 3
= – 21 + 24
= 3
Question no – (65)
Solution :
0 is the only integer which is its own additive inverse.
Two integers whose sum is zero are called additive inverses of each other.
They are also called the negatives of each other.
0 + 0 = 0
Or,
‘Zero’ (0) is its own additive inverse.
Question no – (66)
Solution :
Six distinct integers whose sum is 7 are as follows
(1) 1 + 6
(2) 2 + 5
(3) 3 + 4
(4) 13 + (– 6)
(5) 12 + (– 5)
(6) 11 + (- 4)
Or,
= 1 + 2 + 3 + 6 + (- 2) + (- 3)
= 7
Question no – (67)
Solution :
Let ‘X’ be the integer.
Then ‘– X’ is its additive inverse.
Given that the integer which is 4 more than its additive inverse.
Let ‘X’ = 2
Then additive inverse ‘– X’ = – 2
Difference between additive inverse and integer on number line is 4.
The integer is – 2 + 4 = 2
The integer is 2.
Or,
2 is 4 more than its additive inverse.
So, required integer is 2.
Question no – (68)
Solution :
Let ‘X’ be the integer.
Then ‘–X’ is its additive inverse.
Given that the integer which is 2 less than its additive inverse.
Let ‘X’ = -1
Then additive inverse ‘–X’ = 1
Difference between additive inverse and integer on number line is 2.
The integer is 1 – 2 = -1
The integer is -1.
Or,
-1 is 2 less than its additive inverse.
So, the required integer is -1.
Question no – (69)
Solution :
We write two integers whose sum is less than both the integers.
= – 1 + (- 2)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= – 1 + (-2)
= – 1 – 2
= – 3
Which is less than – 1 and – 2.
Two integers are – 1 and – 2.
Or,
Two integers whose sum is less than both the integers is,
= -2, -3
Question no – (70)
Solution :
We write two distinct integers whose sum is equal to one of the integers.
= 4 + 0
= 4
We adding 4 and 0 whose sum is equal to one (4) of integer.
The integers are 4 and 0.
Or,
Two distinct integers whose sum is equal to one of the integers are,
= 2, 0
Question no – (71)
Solution :
(a) Negative integers are left side.
(b) Positive integers are in right side.
(c) The number on the right is greater.
Question no – (72)
Solution :
= 1 + 2 – 3 + 4 + 5 – 6 + 7 + 8 – 9 = – 5
= 1 + 2 – 3 + 4 + 5 – 6 + 7 + 8 – 9
= 3 – 3 + 9 – 6 + 15 – 9
= 27 – 18
= 9
Question no – (73)
Solution :
Given numbers, -2, 1, 0, -3, +4, -5
In the ascending order = -5, -3, -2, 0, 1, + 4
Question no – (74)
Solution :
Given numbers, -3, 0, -1, -4, -3, -6
In the descending order = 0, -1, -3 , -3 , -4, -6
Question no – (75)
Solution :
We write two integers whose sum is 6 and difference is also 6.
We taking 0 and 6 are two integers.
Adding this two integers
= 0 + 6 = 6
Subtracting this two integers
= 6 – 0 = 6
The two integers are 0 and 6.
Question no – (76)
Solution :
We write five integers which are less than –100 but greater than –150.
-135,-130,-123,-134,-110,-101,-143 these are some answers.
Or,
Five integers which are less than -100 but greater than -150 are,
= -140, -130, -120, -110, -100
Question no – (77)
Solution :
Four pairs of integers which are at the same distance from 2.
(i) 0 and 4 is at same distance from 2 (0, 4) is a pair.
(ii) -1 and 5 is at same distance from 2 (-1, 5) is a pair.
(iii) 1 and 3 is at same distance from 2 (1, 3) is a pair.
(iv) -2 and 6 is at same distance from 2 (-2, 6) is a pair.
Question no – (78)
Solution :
As per the question,
The sum of two integers is = 30.
If one of the integers = -42,
The other integer is = ?
Now, Second integer + (- 42) = 30
∴ Second integer,
= 30 – (- 42)
= 30 + 42
= 72
Thus the other integer is 72
Question no – (79)
Solution :
Sum of two integers is –80.
One of the integers is –90.
Other integer =
= – 90 +? = – 80
? = – 80 + 90
When numbers having + and – sign and addition is there.
We subtract smaller number from larger number and give larger number sign.
? = 90 – 80
? = 10
The other integer is 10.
Or,
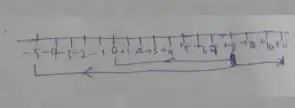
= – 90 + 10
= – 80
∴ The other integer is -10
Question no – (80)
Solution :
(a) –5
We are at 8 on the number line.
We have to move left to reach at -5.
(b) 11
We are at 8 on the number line.
We have to move right to reach at 11.
(c) 0
We are at 8 on the number line.
We have to move left to reach at 0.
Or,
(a) (- 5) to reach -5 we have to move left.
(b) to reach 11 we have to make right.
(c) to reach 0 we have to move left.
Question no – (81)
Solution :
(a) 4 more than – 5
4 more than – 5
We have to add 4 in – 5.
= – 5 + 4
When numbers having + and – sign and addition is there.
We subtract smaller number from larger number and give larger number sign.
= – 5 + 4
= – 1
(b) 3 less than 2
3 less than 2
We have to subtract 3 from 2.
= 2 – 3
= – 1
(c) 2 less than – 2
2 less than – 2
We have to subtract 2 from – 2.
= – 2 – 2
= – 4
Question no – (82)
Solution :
Given, 49 – (– 40) – (– 3) + 69.
= 49 – (– 40) – (– 3) + 69.
= 49 + 40 + 3 + 69 (We doing – x – = +)
= 89 + 72
= 161
Therefore, the value will be 161.
Or,
= 49 – (-40) – (-3) + 69
= 49 + 40 + 3 + 69
= 161
Thus, the value is 161
Question no – (83)
Solution :
We first add [(– 2100) + (– 2001)]
(– 2100) + (– 2001)
= – 2100 – 2001 (We doing + x – = -)
When numbers having same sign and addition is there.
We adding all smaller and larger number and give same (-ve) sign.
= – 2100 – 2001
= – 4101
Now we subtract – 5308 from – 4101
= – 4101 – (– 5308)
= – 4101 + 5308(We doing – x – = +)
When numbers having + and – sign and addition is there.
We subtract smaller number from larger number and give larger number sign.
= 5308 – 4101
= 1207
Therefore, the answer will be 1207.
Next Chapter Solution :