Warning: Undefined array key "https://nctbsolution.com/ncert-exemplar-solutions-class-6-mathematics/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Ncert exemplar Solutions Class 6 Mathematics Fractions and Decimals
Welcome to NCTB Solutions. Here with this post we are going to help 6th class students for the Solutions of NCERT Class 6 Mathematics Book, Unit 4, Fractions. Here students can easily find step by step solutions of all the problems for Fractions, Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get Unit 4 solutions.
Fractions Unit 4 Solution :
Multiple Choice Questions :
Question no – (1)
The fraction which is not equal to 4/5 is
Solution :
40 /50 we divide by 10 we get 4 / 5.
12/ 15 we divide by 3 we get 4 / 5.
16/ 20 we divide by 4 we get 4 / 5.
9 /15 we divide by 3 we get 3 / 5.
The fraction which is not equal to 4/ 5 is 9 /15
Hence, correct answer is option – (D) 9 /15
Question no – (2)
The two consecutive integers between which the fraction 5/7 lies are
Solution :
When numerator is less than denominator then the value of fraction is less than 1.
5/7 here, numerator is less than denominator then the value of fraction is less than 1.
The two consecutive integers between which the fraction 5/7 lies are 0 and 1
Thus, the correct answer is option – (B) 0 and 1
Question no – (3)
When 1/4 is written with denominator as 12, its numerator is
Solution :
When 1/4 is written with denominator as 12, its numerator is 3.
Thus, the correct option is – (A) 3
Question no – (4)
Which of the following is not in the lowest form?
Solution :
Lowest form = after simplification the fraction is not divided by any number.
7 /5, 13/ 33, 27/ 28 is in its lowest form.
But in 15/ 20 it is divided by 5 we get 4/ 5. 15/20 is not in lowest form.
Hence, the correct answer is option – (B) 15/ 20
Question no – (5)
If 5/8 = 20/p = then value of p is
Solution :
5/8 =20/ p
By cross multiplication,
P x 5 = 20 x 8
P x 5 = 160
P = 160 / 5
P = 32
Hence, correct answer is option – (C) 32
Alternative Solution,
5/8 = 20/p
= 5p = 20 × 8
= p = 20 × 8/5
= p = 32
= 32
The correct option is – (C) 32
Question no – (6)
Which of the following is not equal to the others?
Solution :
When numerator of all fractions are same then those fraction have small denominator is the greatest fraction and those fraction having large denominator is smaller fraction.
5/ 6 is a small denominator hence it is greatest fraction.
The correct answer is option – (B) 5/ 6
Question no – (7)
Which of the following fractions is the greatest?
Solution :
When numerator of all fractions are same then those fraction have small denominator is the greatest fraction and those fraction having large denominator is smaller fraction.
5/ 6 is a small denominator hence it is greatest fraction.
Hence, the correct answer is option – (B) 5/ 6
Question no – (8)
Which of the following fractions is the smallest?
Solution :
When denominator is same then those fractions having larger numerator is greatest fraction and those fraction having small numerator is smaller fraction.
3/ 8 having smaller numerator hence, it is smaller fraction.
Hence, correct answer is option – (C) 3/ 8
Question no – (9)
Sum of 4/17 and 15/17 is
Solution :
When denominator is same we doing addition and subtraction of fractions.
4 /17 + 15/ 17 = 19 / 17
Thus, the correct answer is option – (A) 19/17
Alternative Solution,
= 4/17 + 15/17
= 4 + 15/17
= 19/17
The correct option is – (A) 19/17
Question no – (10)
On subtracting 5/9 from 19/9, the result is
Solution :
When denominator is same we doing addition and subtraction of fractions.
19/9 – 5/9 = 14/9
So, the correct answer is option – (B) 14/9
Alternative Solution,
= 19/9 – 5/9
= 19 – 5/9
= 14/9
The correct option is – (B) 14/9
Question no – (11)
0.7499 lies between
Solution :
0.7499 lies between 0.749 and 0.75
Thus, the correct answer is option – (C) 0.749 and 0.75
Question no – (12)
0.023 lies between
Solution :
0.023 lies between 0.02 and 0.03
Hence, correct answer is option – (B) 0.02 and 0.03
Question no – (13)
11/7 can be expressed in the form
Solution :
11/7 = we expressed in mixed fraction.
We divide by 7 we get,
[1 x 4/7]
Hence, the correct answer is option – (C) 1 4/7
Question no – (14)
The mixed fraction 5 4/7 can be expressed as
Solution :
The mixed fraction 5 4/ 7 can be expressed as
First we do multiplication and then addition.
= [5 x 4/ 7] = [5 x 7] + 4 / 7
= 35 + 4 / 7
= 39/7
The correct answer is option – (B) 39/7
Question no – (15)
0.07 + 0.008 is equal to
Solution :
Addition of decimal
We put decimal point below of each other and then addition is then.
0.070
+ 0.008
—————-
0.078
The correct answer is option – (C) 0.078
Question no – (16)
Which of the following decimals is the greatest?
Solution :
0.182 lies between 0.1 to 0.2
0.0925 lies between 0.01 to 0.1
0.29 lies between 0.2 to 0.3
0.038 lies between 0.01 to 0.1
From above 0.29 is the greatest decimal.
Hence, correct answer is option (C) 0.29
Alternative Solution,
0.0182 = 182/1000, 0.0925
= 925/10000, 0.29
= 29/100, 0.038
= 38/1000
= 10000 ÷ 1000 = 10 182 ×10/1000 × 10 = 1820/10000
= 10000 ÷ 10000 = 1 = 925 × 1/10000 × 1 = 925/10000
= 10000 ÷ 100 = 100 = 29 × 100/100 × 100 = 2900/10000
= 10000 ÷ 1000 = 10 = 38 × 10/1000 × 10 = 380/10000
∴ Greatest is 2900/10000 i.e. 0.29
Question no – (17)
Which of the following decimals is the smallest?
Solution :
0.27 lies between 0.2 to 0.3
1.5 lies between 1 to 2
0.082 lies between 0.01 to 0.1
0.103 lies between 0.1 to 1
From above 0.082 is the smallest decimal.
Thus, the correct answer is option – (C) 0.082
Alternative Solution,
0.27 = 27/100, 1.5 = 15/10, 14.5 = 145/100, 13.6 = 136/10
100 ÷ 100 = 1 = 27 × 1/100 × 1 = 27/100
100 ÷ 10 = 10 = 15 × 10/10 × 10 = 150/100
100 ÷ 10 = 10 = 145 × 10/10 × 10 = 1450/100
100 ÷ 10 = 10 = 136 × 10/10 × 10 = 1360/100
∴ The smallest 27/100 i.e. = 0.27
Question no – (18)
13.572 correct to the tenths place is
Solution :
13.572 correct to the tenths place =
At tenth place 7 is there. Which is greater than 5.
Hence,
13.572 correct to the tenths place = 13.6
So, the correct answer is option – (D) 13.6
Question no – (19)
15.8 – 6.73 is equal to
Solution :
Subtraction of decimal,
We put decimal point below of each other and then subtraction is then.
15.80
– 6.73
————–
9.07
The correct answer is option – (B) 9.07
Question no – (20)
The decimal 0.238 is equal to the fraction
Solution :
0.238 having value less than one.
Value less than one is only when numerator is less than denominator.
119/500 is the only option having numerator is less than denominator.
Hence, correct answer is option – (A) 119/500
Fill in the blanks :
Question no – (21)
Solution :
A number representing a part of a whole is called a fraction.
E.g. 5/ 7
Denominator is 7 which is Total (whole) parts of any.
Numerator is 5 which is 5 parts out of whole (total).
Question no – (22)
Solution :
A fraction with denominator greater than the numerator is called a Proper fraction.
E.g. 5/8
Denominator 8 is greater than numerator 5.
Question no – (23)
Solution :
Fractions with the same denominator are called Like fractions.
E.g. 2 /18 and 4/18
Question no – (24)
Solution :
13 5/18 is a mixed fraction.
= [13 5/18]
= 13 x 18 + 5 / 18
= 239/18
Question no – (25)
Solution :
18/5 is an improper fraction.
Question no – (26)
Solution :
7/19 is a Proper fraction.
A fraction with denominator greater than the numerator is called a Proper fraction.
Question no – (27)
Solution :
5/8 and 3/8 are Like proper fractions.
Fractions with the same denominator are called Like fractions.
Question no – (28)
Solution :
6/11 and 6/13 are Unlike proper fractions.
Fractions with the same numerator are called Unlike fractions.
Question no – (29)
Solution :
The fraction 6/15 in simplest form is
6/15 = we divide both numerator and denominator by 3.
We get, 2/ 5
The fraction 6/15 in simplest form is 2/5
Question no – (30)
Solution :
The fraction 17/34 in simplest form is 1/ 2
17/34 = we divide both numerator and denominator by 17.
We get,1/ 2.
The fraction 17/34 in simplest form is 1/ 2.
Question no – (31)
Solution :
18/135 and 90/675 are proper, unlike and Equivalent fractions.
18/135 we multiply given fraction by 5.
We get, 18 x 5 /135 x 5 = 90/675
This are called Equivalent fraction.
Question no – (32)
Solution :
8 2/7 is equal to the improper fraction 58/7.
[8 2/7] is a mixed fraction. We convert it as improper fraction.
[8 2/7] = 7 x 8 + 2 / 7
[8 2/7] = 56 + 2 /7
[8 2/7] = 58 /7
Question no – (33)
Solution :
87/7 is equal to the mixed fraction 12 3/7
87/7 is improper fraction we convert it as mixed fraction.
87/7 = we divide it by 7.
We get, 12 x 3 / 7
= [12 3 / 7]
Question no – (34)
Solution :
9 + 2/10 + 6/100 is equal to the decimal number 9.26
Decimal fraction is divided by 10, then decimal-sign moves one decimal place left side.
We are moving 1 decimal sign left side.
2/10 = 0.2
Decimal fraction is divided by 100, then decimal-sign moves two decimal place left side.
We are moving 2 decimal sign left side.
= 6/100 = 0.06
= 9 + 0.2 + 0.06
= 9.26
Question no – (35)
Solution :
Decimal 16.25 is equal to the fraction 65/4.
Given, 16.25
There is 2 decimal point. We divide by 100
1625 /100 this is improper fraction.
We divide both by 25
1625 /100 = 65/4
16.25 = 65/4
Question no – (36)
Solution :
Fraction 7/25 is equal to the decimal number 0.28
7/25 is a fraction.
We multiply both numerator and denominator by 4
We get,
7 x 4 /25 x 4 = 28 / 100
28 / 100
Decimal fraction is divided by 100, then decimal-sign moves two decimal place left side.
We are moving 2 decimal sign left side.
28 / 100 = 0.28
Fraction 7/25 is equal to the decimal number 0.28.
Question no – (37)
Solution :
17/9 + 41/9 = 58/9
When denominator is same we do addition or subtraction.
= 17 /9 + 41/9 = 17 + 41 / 9
= 58 / 9 or [6 x 4 / 9]
= 17 /9 + 41/9
= 58 / 9 or [6 x 4/9]
Question no – (38)
Solution :
When denominator is same we do addition or subtraction.
= 67 /14 – 24/14
= 67 – 24/14
= 43 / 14 or [3 x 1/14]
= 67 /14 – 24/14
= 43/14 or [3 x 1/14]
Question no – (39)
Solution :
First we convert mixed fraction into improper fraction.
3 1/2 = 3 x 2 + 1 / 2
3 1/2 = 7 / 2
Now we add 17/2 + 7 / 2
When denominator is same we do addition or subtraction.
= 17/2 + 7 / 2 = 17 + 7 /2
= 24 / 2
= 12
= 17/2 + 3 1/2 = 12
Question no – (40)
Solution :
9 1/4 – 5/4 = 8
First we convert mixed fraction into improper fraction.
9 1/4 = 9 x 4 + 1/4
9 1/4 = 37/4
Now we subtract 5/4 from 37/4
37/4 – 5/4
When denominator is same we do addition or subtraction.
= 37/4 – 5/4
= 37- 5/4
= 32/4
= 8
Question no – (41)
Solution :
4.55 + 9.73 = 14.28
We adding 4.55 + 9.73
4.55
+ 9.73
————
14.28
Question no – (42)
Solution :
8.76 – 2.68 = 6.08
We subtract 8.76 – 2.68
8.76
– 2.68
————–
6.08
Question no – (43)
Solution :
The value of 50 coins of 50 paisa = Rs.25
50 coins of 50 paisa = 50 x 50 = 2500 paise
We know, 1 rupees = 100 paise
2500 paise = 2500/100 = 25 Rupees.
The value of 50 coins of 50 paisa = Rs.25
Question no – (44)
Solution :
3 Hundredths + 3 tenths = 0.33.
3 Hundredths = 3 / 100
Decimal fraction is divided by 100, then decimal-sign moves two decimal place left side.
We are moving 2 decimal sign left side.
3 / 100 = 0.03
3 tenths = 3/10
Decimal fraction is divided by 10, then decimal-sign moves one decimal place left side.
We are moving 1 decimal sign left side.
3/10 = 0.3
Addition of 0.03 + 0.3
= 0.03 + 0.3
= 0.33
3 Hundredths + 3 tenths = 0.33
State whether the statement is true or false :
Question no – (45)
Solution :
Fractions with same numerator are called like fractions – False
Correct statement :
Fractions with same denominator is called like fractions.
Question no – (46)
Solution :
Fraction 18/39 is in its lowest form – False.
Because,
Fraction 18/39 is not in its lowest form.
18/39 we divide both by 3.
18/39 = 6/13
6/13 is lowest form.
Question no – (47)
Solution :
Fractions 15/39 and 45/117 are equivalent fractions – True.
15/39 = we multiply both by 3
We get,
= 15 x 3/39 x 3
= 45/117
Fractions 15/39 and 45/117 are equivalent fractions
Alternative Solution,
15/13 = 5/13
45/117 = 5/13
The lowest form of two fractions are same.
So, the two fractions are equivalent fractions.
Thus, the statement is True.
Question no – (48)
Solution :
The sum of two fractions is always a fraction – False.
Because,
The sum of two fractions is not always a fraction.
E.g.
= 2/3 + 1/3
= 3/3
= 1 (is not a fraction)
Question no – (49)
Solution :
The result obtained by subtracting a fraction from another fraction is necessarily a fraction – False.
Because,
The result obtained by subtracting a fraction from another fraction is not necessarily a fraction.
E.g. = 4/3 – 1/3
= 3/3
= 1
Alternative Solution,
Given statement is False.
Let, two fraction 1/2 and 5/2
Sum of them = 1/2 + 5/2
= 1 + 5/2
= 6/2
= 3 which is not a fraction
Therefore, sum of two fraction is not always fractions.
Question no – (50)
Solution :
Given statement is False.
Let, the us take two fraction 5/2, 1/2
Subtracting them,
= 5/2 – 1/2
= 5 – 7/2
= 4/2
= 2 which is not a fraction.
Therefore, result obtained by subtractions a fraction from another fraction is not necessarily a fraction.
Question no – (51)
Solution :
Given statement is False.
Let, us take a digit = 54
The digit of one’s place is 4
and the place value of digit tenth’s place = 50
= 50 is not 10 time of 4.
Alternative Solution,
Given statement is False,
Because, The place value of a digit at the tenths place is not 10 times the same digit at the ones place.
Question no – (52)
Solution :
Given statement is True.
Let, us take a digit = 550
The place value of tenth place is = 50
The place value of hundred place is = 500
∴ 500 × 1/10 = 50
Question no – (53)
Solution :
Given statement is False.
3.725 = 3.73
Therefore, 3.725 is not equal to 3.72 correct to two decimal places.
Question no – (54)
Solution :
Given statement is True.
= 25/8 ÷ 25 = 13.125
∴ 25/8 = 3.125
Question no – (55)
Solution :
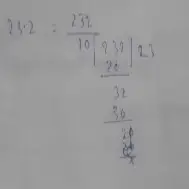
The decimal 23.2 = 23 2/5 – This statement is False.
Because,
= 23.2 here, 1 decimal point we divide by 10.
= 232 / 10
= [23 2/10]
The decimal 23.2 = [23 2/10]
Alternative answer,
Given statement is False.
23.2
∴ 23.2 = 23 2/10
Question no – (58)
Solution :
25/19 + 6/19 = 31/38 – This solution is False.
Because,
When denominator is same we do addition and subtraction.
25 /19+ 6/19 = 31/19
Question no – (59)
Solution :
Given statement is False.
Because, 8/18 – 8/15
= 40 – 48/90
= -8/90
Question no – (60)
Solution :
7/12 + 11/12= 3/2 – This solution is True.
Because,
When denominator is same we do addition and subtraction.
7 /12 + 11/12= 7 + 11 /12 = 18 /12
We divide both by 6 we get,
= 3/2
= 7 /12 + 11/12 = 3/2
Question no – (61)
Solution :
3.03 + 0.016 = 3.019 – This solution is False.
Because,
3.030
+ 0.016
—————–
3.046
3.03 + 0.016 = 3.046
Question no – (62)
Solution :
Given statement is True.
42.28
-3.19
———-
39.09
Question no – (63)
Solution :
16/25 > 13/25 – This statement is True.
Question no – (64)
Solution :
19.25 < 19.053 – This statement is False.
Because, here, 19.25 is greater than, 19.053 19.25 > 19.053
Question no – (65)
Solution :
Given statement is True.
13.730 = 13.73
Fill in the blanks using ‘>’, ‘<’ or ‘=’ :
Question no – (66)
Solution :
Given, 11/16 _ 14/15
= 240 ÷ 16 = 15 11 × 15/16 × 15 = 165/240
= 240 ÷ 15 = 16 14 × 16/15 × 16 = 224/240
∴ 11/16 < 14/15
Question no – (67)
Solution :
Given, 8/15 _ 95/14
= 210 ÷ 15 = 14 8 × 14/15 × 14 = 112/210
= 210 ÷ 14 = 15 95 × 15 /14 × 15 = 1425/210
∴ 8/15 < 95/14
Question no – (68)
Solution :
Given, 12/75 _ 32/200
= 600 ÷ 75 = 8 12 × 8/75 × 8 = 96/600
= 600 ÷ 200 = 3 32 × 3/200 × 3 = 96/600
∴ 12/75 = 32/200
Question no – (69)
Solution :
Given, 3.25 _ 3.4
= 3.25 = 325/100
= 3.4 = 34/10
= 100 ÷ 100 = 1 325 × 1/100 × 1 = 325/100
= 100 ÷ 10 = 10 34 × 10/10 × 10 = 340/100
∴ 3.25 < 3.4
Question no – (70)
Solution :
Given, 18/15 _ 1.3
= 18/15 = 6/5,
= 1.3 = 13/10
= 10 ÷ 5 = 2 6 × 2/56 × 2 = 12/10
= 10 ÷ 10 = 1 13 × 1/10 × 1 = 13/10
∴ 18/15 < 1.3
Question no – (71)
Solution :
Given, 6.25 _ 25/4
= 6.25 = 625/100,
= 25/4 = 25/4
= 200 ÷ 100 = 2 625 × 2/100 × 2 = 1250/200
= 200 ÷ 4 = 50 25 × 50/4 × 50 = 1250/200
∴ 6.25 = 25/4
Question no – (72)
Solution :
The fraction represented by the shaded portion of the adjoining figure is 7/8
Question no – (74)
Solution :
Ali divided one fruit cake equally among six persons.
Denominator is 6.
Part of the cake he gave to each person = each person get 1 part of cake.
Numerator is 1.
Part of the cake he gave to each person = 1/6
Thus, he gave 1/6 part of the cake to each person.
Question no – (75)
Solution :
Given, 12, 142, 12, 124, 12.104, 12,401 , 12, 214
= 12142/1000, 12124/1000, 12104/1000, 12401/1000, 12214/1000
∴ In ascending order,
12,104, 12124, 12,142, 12.214, 12, 401
Question no – (76)
Solution :
Largest four digit decimal number using digits 1, 5, 3 and 8 once = 0.8531
Question no – (77)
Solution :
Smallest four digit decimal number using digits 2, 4, 5 and 3 once = 0.2345
Question no – (78)
Solution :
11/20 we multiply given fraction by 5
We get, 11 x 5 /20 x 5 = 55 / 100
Decimal fraction is divided by 100, then decimal-sign moves two decimal place left side.
We are moving 2 decimal sign left side.
= 55 / 100 = 0.55
= 11/20 = 0.55
Question no – (79)
Solution :
6 2/3 this is mixed fraction we convert it into improper fraction.
[6 x 2/3] = 3 x 6 + 2 / 3
[6 x 2/3] = 18 + 2 / 3
[6 x 2/3] = 20 / 3
Question no – (80)
Solution :
3 2/5 this is mixed fraction we convert it into improper fraction.
[3 x 2/5] = 5 x 3 + 2 / 5
[3 x 2/5] = 15 + 2 / 5
[3 x 2/5] = 17 / 5
Now, we multiply given fraction by 20
We get,
= 17 x 20 / 5 x 20
= 85 / 100
Decimal fraction is divided by 100, then decimal-sign moves two decimal place left side.
We are moving 2 decimal sign left side.
85 / 100 = 0.85
3 2/5 = 0.85
Question no – (81)
Solution :
0.041 is a decimal fraction we convert it into fraction.
0.041 containing 3 decimal point.
We divide by 1000
0.041 = 41 / 1000
Question no – (82)
Solution :
6.03 is a decimal fraction we convert it into mixed fraction.
6.03 containing 2 decimal point.
We divide by 100
= 6.03 = 603/100
= 603/100 = [6 x 3/100]
= 6.03 = [6 x 3/100]
Question no – (83)
Solution :
As we know, 1000 gm. = 1 Kg.
1 g = 1 /1000 Kg.
5201 g = 5201 / 1000 kg
5201 g = 5.201 kg
Question no – (84)
Solution :
We know, 100 paise = 1 Rupees
1 paise = 1 / 100 Rupees
2009 paise = 2009 / 100 Rupees
= 2009 / 100 Rupees
We divide by 100
We get, 2009 paise = [20 x 9/100]
Alternative Solution,
Given, 2009 paise
= 2009/100 Rupees
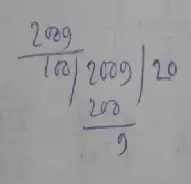
∴ 20 9/100
Question no – (85)
Solution :
We know, 100 cm. = 1 m.
1 cm = 1 /100 m.
1537 cm = 1537 /100 m
1537 /100 m this is improper fraction.
Now, Decimal fraction is divided by 100, then decimal-sign moves two decimal place left side.
We are moving 2 decimal sign left side.
= 1537 /100 m = 15.37 m
Alternative Solution,
We know that, 1 m = 100 cm
∴ 1537/100 m
= 15.37 m
Question no – (86)
Solution :
We know,
1000 m. = 1 Km.
1 m = 1 /1000 Km.
2435 m = 2435 /1000 m
2435 /1000 m this is improper fraction.
We divide by 1000
We get, 2435 /1000 = [2 x 435 /1000]
Alternative Solution,
Given, 2435 m
= 2435/1000 km
= 2.435 km
= 2 435/1000 km
Question no – (87)
Solution :
Ascending order is the order in which fractions are arranged from smaller to larger.
2/3, 3/4, 1/ 2 and 5/6
We are using cross multiplication method.
We multiply 2 with 4.
We multiply 3 with 3.
We multiply 1 with 6.
We multiply 2 with 5.
(i) 2 x 4 = 8
(ii) 3 x 3 = 9
(iii) 1 x 6 = 6
(iv) 2 x 5 = 10
We are arranging in Ascending order.
(iii) < (i) < (ii) < (iv)
1/2 < 2/3 < 3/4 < 5/6
Alternative Solution,
Given, 2/3, 3/4, 1/2 , 5/6
= 12 ÷ 3 = 4 2 × 4/3 × 4 = 8/12
= 12 ÷ 4 = 3 3 × 3/4 × 3 = 9/12
= 12 ÷ 2 = 6 1 × 6/2 × 6 = 6/12
= 12 ÷ 6 = 2 5 × 2/6 ×2 = 10/12
∴ In ascending order,
= 1/2 , 2/3, 3/4., 5/6
Question no – (88)
Solution :
Descending order is the order in which fractions are arranged from larger to smaller.
6 /7, 7/ 8, 4/5 and 3/4
We are using cross multiplication method.
We multiply 6 with 8.
We multiply 7 with 7.
We multiply 4 with 4.
We multiply 5 with 3.
(i) 6 x 8 = 48
(ii) 7 x 7 = 49
(iii) 4 x 4 = 16
(iv) 5 x 3 = 15
We are arranging in descending order.
(ii) > (i) > (iii) > (iv)
7/8 > 6/7 > 4/5 > 3/4
Alternative Solution,
Given, 6/7, 7/8, 4/5, 3/4
= 280 ÷ 7 = 40 6 × 40/7 × 40 = 240/280
= 280 ÷ 8 = 35 7 × 35/8 × 35 = 245/280
= 280 ÷ 5 = 56 4 × 56/5 × 56 = 224/280
= 280 ÷ 4 = 70 3 × 70/4 ×70 = 210/280
∴ In descending order,
= 7/8, 6/7, 4/5, 3/4,
Question no – (89)
Solution :
3/4 as a fraction with denominator 44
To get denominator 44 we multiply both by 11.
We get, 3 x 11 /4 x 11
= 33 / 44
= 33 / 44
Alternative Solution,
3/4 as a fraction with denominator 44,
= 3 × 11/4 × 11
= 33/44
Question no – (90)
Solution :
5/6 as a fraction with numerator 60.
To get numerator 60 we multiply both by 12
We get, 5/6 = 5 x 12 /6 x 12
= 60 / 72
Alterunative solution,
5/6 as a fraction with numerator 60,
= 5 × 12/6 × 12
= 60/72
Question no – (91)
Solution :
Given, 129/8
We convert given fraction into mixed fraction.
We divide fraction by 8.
We get, 129/8 = [16 x 1/8]
Question no – (92)
Solution :
Given, 20.83
We have to rounding off it to nearest tenths
0.83 is less than 0.85
We rounding off 20.83 at tenth place = 20.8
Question no – (93)
Solution :
Given, 75.195
We have to rounding off it to nearest hundredths.
0.195 is greater than 0.150
We rounding off 75.195 nearest hundredths is 75.200
Question no – (94)
Solution :
Given, 27.981
We have to rounding off it to nearest tenths.
0.98 is greater than 0.50
We rounding of it as 1
We add this 1 in 27
27.981 = 28.00
We rounding off 27.981 at tenth place = 28.00
Question no – (95)
Solution :
Addition of 3/8 and 2/3.
Here, denominator of both the fractions are different. So, we add them by converting into like fraction.
For this, we find LCM of 8 and 3.
Factor of 8 = 1 x 8
Factor of 3 = 1 x 3
LCM is multiplication of common and uncommon factors.
LCM of 8 and 3 = 1 x 8 x 3 = 24
LCM of 8 and 3 is 24.
Making denominator of both fractions is 24.
3/8 = 3 x 3 / 8 x 3 = 9/24
(Multiplying numerator and denominator by 3, to make the denominator 24.)
2 / 3 = 2 x 8 / 3 x 8 = 16 / 24
(Multiplying numerator and denominator by 8, to make the denominator 24.)
Now, 9/24 and 16 /24 are like fractions.
9/24 + 16/24 = 25 / 24
= [1 1/24]
Addition of 3/8 + 2/3 is 25 / 24 or [1 1/24]
Alternative solution,
Given, fractions 3/8 and 2/3.
∴ 3/8 + 2/3
= 9 + 16/24
= 25/24
Question no – (96)
Solution :
First we convert mixed fraction into fraction.
= 6 3/4 = 6 x 4 + 3 / 4
= 27 /4
We add 3/8 + 27 / 4
Here, denominator of both the fractions are different. So, we add them by converting into like fraction.
For this, find LCM of 4 and 8.
Factor of 4 = 1 x 2 x 2
Factor of 8 = 1 x 2 x 2 x 2
LCM is multiplication of common and uncommon factors.
LCM of 4 and 8 = 2 x 2 x 2 = 8
LCM of 4 and 8 is 8.
Making denominator of both fractions is 8.
27/4 = 27 x 2 / 4 x 2 = 54 /8
(Multiplying numerator and denominator by 2, to make the denominator 8.)
3 / 8 = 3 x 1 / 8 x 1 = 3 /8
(Multiplying numerator and denominator by 1, to make the denominator 8.)
Now, 54/8 and 3 /8 are like fractions.
54/8 + 3/8 = 57 / 8
= [7 1/8]
Addition of 3/8 + 6 3/4.is 57 / 8 or [7 1/8]
Alternative Solution,
Given, fractions 3/8 and 6 3/4.
∴ 3/8 + 6 3/4
= 3/8 + 27/4
= 3 + 54/8
= 57/8
= 7 1/8
Question no – (97)
Solution :
Given, 1/2 – 1/6
Here, denominator of both the fractions are different. So, we Subtract them by converting into like fraction.
For this, find LCM of 2 and 6.
Factor of 2 = 1 x 2
Factor of 6 = 1 x 2 x 3
LCM is multiplication of common and uncommon factors.
LCM of 2 and 6 = 1 x 2 x 3 = 6
LCM of 2 and 6 is 6.
Making denominator of both fractions is 6.
1/2 = 1 x 3 / 2 x 3 = 3/6
(Multiplying numerator and denominator by 3, to make the denominator 6.)
1 / 6 = 1 x 1 / 6 x 1 = 1 /6
(Multiplying numerator and denominator by 1, to make the denominator 6.)
Now, 3/6 and 1 /6 are like fractions.
3/6 – 1/6 = 2/ 6
= 1/3
Subtraction of 1/2 – 1/6 is 1/3.
Alternative Solution,
Given, 1/6 from 1/2.
∴ 1/2 – 1/6
= 6 – 2/12
= 4/12
= 1/3
Question no – (98)
Solution :
First we convert mixed fraction into fraction.
8 1/3. = 8 x 3 + 1 / 3
= 25 / 3
We subtract 25/3 from 100/ 9
100/9 – 25 / 3
Here, denominator of both the fractions are different. So, we Subtract them by converting into like fraction.
For this, find LCM of 9 and 3.
Factor of 9 = 1 x 3 x 3
Factor of 3 = 1 x 3
LCM is multiplication of common and uncommon factors.
LCM of 9 and 3 = 1 x 3 x 3 = 9
LCM of 9 and 3 is 9.
Making denominator of both fractions is 9.
100/9 = 100 x 1 / 9 x 1 = 100 /9
(Multiplying numerator and denominator by 1, to make the denominator 9.)
25 / 3 = 25 x 3 / 3 x 3 = 75 /9
(Multiplying numerator and denominator by 3, to make the denominator 9.)
Now, 100/9 and 75 /9 are like fractions.
100/9 – 75/9 = 25/ 9
= 25/9 = [2 7/9]
Subtraction of 100/9 – 25 / 3 is 25/9 or [2 7/9]
Alternative Solution,
Given, 8 1/3 from 100/9.
∴ 100/9 – 8 1/3
= 100/9 – 25/3
= 100 – 75/9
= 25/9
= 2 7/9
Question no – (99)
Solution :
First we convert mixed fraction into fraction.
= 1 1/4. = 1 x 4 + 1 / 4
= 5 / 4
= 6 1/2 = 6 x 2 + 1 / 2
= 13 / 2
= 13 / 2 – 5 / 4
Here, denominator of both the fractions are different. So, we subtract them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
13/2 = 13 x 2 / 2 x 2 = 26 /4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
5 / 4 = 5 x 1 / 4 x 1 = 5 /4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
Now, 26/4 and 5 /4 are like fractions.
26/4 – 5/4 = 21/ 9
= 21/9 = [2 1/3]
Subtraction of 13 / 2 – 5 / 4 is 21/9 or [2 1/3]
Alternative Solution,
Given, 1 1/4 from 6 1/2.
∴ 6 1/2 – 1 1/4
= 13/2 – 5/4
= 26 – 5/4
= 21/4
= 5 1/4
Question no – (100)
Solution :
First we convert mixed fraction into fraction.
∴ 1 1/4. = 1 x 4 + 1 / 4 = 5 / 4
∴ 6 1/2 = 6 x 2 + 1 / 2 = 13 / 2
= 5/4 + 13 /2
Here, denominator of both the fractions are different. So, we subtract them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
∴ 5 / 4 = 5 x 1 / 4 x 1 = 5 /4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
∴ 13/2 = 13 x 2 / 2 x 2 = 26 /4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
Now, 5/4 and 26 /4 are like fractions.
= 5/4 + 26/4 = 31 /4
= 31 /4 = [7 ¾]
Addition of 5/4 + 13 /2 is 31 /4 or [7 3/4]
Alternative Solution,
Given, 1 1/4 and 6 1/2
∴ 1 1/4 + 6 1/2
= 5/4 + 13/2
= 5 + 26/4
= 31/4
= 7 3/4
Question no – (101)
Solution :
Katrina rode her bicycle 6 1/2 km in the morning.
In fraction 6 1/2 km
= 6 x 2 + 1 /2
= 13 / 2 km
Katrina rode her bicycle 8 3/4km in the evening.
In fraction 8 3/4km
= 8 x 4 + 3 / 4
= 35 /4 km
The distance travelled by her altogether on that day = 13 / 2 km + 35 /4 km
Here, denominator of both the fractions are different.
So, we subtract them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
13/2 = 13x 2 / 2 x 2 = 26 /4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
35 / 4 = 35 x 1 / 4 x 1 = 35 /4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
Now, 26 /4 and 35 /4 are like fractions.
26/4 + 35/4 = 61 /4
= 61 /4
= [15 1/4]
The distance travelled by her altogether on that day is [15 1/4] km.
Alternative Solution,
The distance travelled by Katrina is,
= 6 1/2 km + 83/4 km
= (13/2 + 35/4) km
= 26 35/4 km
= 61/4 km
= 15 1/4 km
Question no – (102)
Solution :
A rectangle is divided into certain number of equal parts.
1/4 fraction = 16 parts of rectangle.
Total parts of rectangle = 16 x 4 = 64.
Total parts of rectangle is 64.
Alternative Solution,
1/4 = 16/?
= 1 × 16/4 × 16
= 16/64
∴ The rectangle bas been divided 64 path.
Question no – (103)
Solution :
Grip size of a tennis racquet is 11 9/80 cm.
11 9/80 cm, we convert this fixed fraction into improper fraction.
11 9/80 cm = 11 x 80 + 9 / 80
= 889 / 80 cm
= 11 9/80 cm = 889 / 80 cm
Alternative Solution,
Given, 11 9/80 cm
∴ 11 9/80 cm
= 889/80 cm
Question no – (104)
Solution :
On an average 1/10 of the food eaten is turned into organism’s own body and is available for the next level of consumer in a food chain.
Total 10 parts out of only 1 is turned into organism’s own body and is available for the next level of consumer in a food chain.
Out of 10 parts 9 parts is not available for the next level.
Fraction of the food eaten is not available for the next level is 9/10.
Question no – (105)
Solution :
Mr. Rajan got a job at the age of 24 years.
He got retired from the job at the age of 60 years.
His total job years = 60 – 24 = 36 years.
Out of 60 years he is doing 36 years job.
Fraction of his age till retirement was he in the job
= 36/60
= 3/5
Fraction of his age till retirement was he in the job is 3/5.
Alternative Solution :
The fraction of his age till retirement in the Job is,
= 60 – 24/60
= 36/60 = 6/10
= 6/10 = 3/5
= 3/5
Question no – (106)
Solution :
In days there are total 24 hours.
The food we eat remains in the stomach for a maximum of 4 hours.
Fraction of a day, does it remain there = 4 / 24 = 1/6 hours.
Alternative Solution :
We know, A day = 24 hour
∴ 4/24
= 1/6 of a day, does it remain there.
Question no – (107)
Solution :
Let ‘X’ be added 25.5 to get 50
X + 25.5 = 50
X = 50 – 25.5
50.0
– 25.5
————-
24.5
X = 24.5
24.5 is added to 25.5 to get 50.
Alternative Solution :
As per question, (50 – 25.5)
50
25.5
———–
24.5
∴ 24.5 be added to 25.5 to get 50.
Question no – (108)
Solution :
Alok purchased 1 kg 200 g potatoes,250 g dhania, 5 kg 300 g onion,500 g palak and 2 kg 600 g tomatoes.
total weight of his purchases in kilograms = 1 kg 200 g potatoes +250 g dhania + 5 kg 300 g onion + 500 g palak + 2 kg 600 g tomatoes.
1 kg 200 g
+ 250 g
+ 5 kg 300 g
+ 500 g
+ 2 kg 600 g
————————
9 kg 850 g
Total weight of his purchases in kilograms is 9 kg 850 g
Question no – (109)
Solution :
Given, 0.011, 1.001, 0.101, 0.110
= 11/1000, 1001/100, 101/1000, 110/1000
∴ In ascending order,
= 0.011, 0.10, 0.110, 1001
Question no – (110)
Solution :
20.02
+ 2.002
————–
22.022
So, the sum is 22.022
Question no – (111)
Solution :
(i) The quantity of diesel saved to the quantity of petrol saved.
33000 tonnes of CNG, 3300 tonnes of diesel and 21000 tonnes of petrol was saved by the end of year 2007.
Fraction of quantity of diesel saved to the quantity of petrol saved.
Quantity of diesel saved = 3300 tonnes
Quantity of petrol saved = 21000 tonnes
Fraction of quantity of diesel saved to the quantity of petrol saved.
= 3300 /21000
Fraction of quantity of diesel saved to the quantity of petrol saved.
= 33/210
= 11/70
Fraction of quantity of diesel saved to the quantity of petrol saved is 11/70.
(ii) The quantity of diesel saved to the quantity of CNG saved.
Quantity of diesel saved = 3300 tonnes
Quantity of CNG saved = 33000 tonnes
Fraction of quantity of diesel saved to the quantity of CNG saved = 3300 /33000
Fraction of quantity of diesel saved to the quantity of CNG saved = 1/10
Fraction of quantity of diesel saved to the quantity of CNG saved is 1/10
Alternative Solution,
(i) The fraction of the quantity of diesel saved to the quantity of patrol saved,
= 3300/21000
= 11/70
(ii) The fraction of the quantity of diesel saved to the quantity of CNG saved,
= 3300/33000
= 1/10
Question no – (112)
Solution :
Which food provides the least energy and which provides the maximum?
= Milk provides the least energy and Rice provides the maximum energy.
Express the least energy as a fraction of the maximum energy.
Least energy = 3.0 joule
Maximum energy = 5.3 joule
Fraction of least to maximum energy
= 3.0/5.3
= 30/53
Question no – (113)
Solution :
A cup is 1/3 full of milk.
Total 3 part of cup. Out of which 1 part is filled with milk.
Remaining part is still left to full the glass by milk
= 3/3 – 1/3
= 2/3
= 2/3 part is still left to full the glass by milk.
Alternative Solution,
1 – 1/3
= 3 – 1/3
= 2/3
∴ 2/3 of cup is to be filled by milk to make it full.
Question no – (114)
Solution :
Mary bought 3 1/2 m of lace.
In fraction, 3 1/2 m = 3 x 2 + 1/2 = 7/2 m
She used 1 3/4 m of lace for her new dress.
In fraction, 1 3/4 m = 1 x 4 + 3 /4 = 7/4 m
Lace is left with her = 7/2 m – 7/4 m
Here, denominator of both the fractions are different. So, we subtract them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
7/ 2= 7 x 2 / 2 x 2 = 14 / 4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
7 / 4 = 7 x 1 / 4 x 1 = 7 / 4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
Now, 14/4 and 7 /4 are like fractions.
= 14/4 – 7 /4
= 7/4
= 1 3/4 m
Lace is left with her is 1 3/4 m
Alternative Solution,
= (3 1/2 – 1 3/4) m
= (7/2 – 7/4) m
= 14 – 7/4
= 7/4 m
= 1 3/4
∴ 1 3/4 m lace is left with her.
Question no – (115)
Solution :
= 46 3/8 + 1 1/4
= 371/8 + 5/4
= 371 + 10/8
= 381/8
= 47 5/8
∴ Her weight was 47 5/8 kg on Monday
Question no – (116)
Solution :
Sunil purchased 12 1/2 litres of juice on Monday
In fraction, 12 1/2 litres = 12 x 2 + 1/2 = 25 /2 Litre.
14 3/4 litres of juice on Tuesday.
In fraction, 14 3/4 litres = 14 x 4 + 3 /4 = 59/4 Litre.
Litres of juice did he purchase together in two days = 25 /2 Litre + 59/4 Litre.
Here, denominator of both the fractions are different. So, we add them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
25/ 2 = 25 x 2 / 2 x 2 = 50 / 4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
59 / 4 = 59 x 1 / 4 x 1 = 59 / 4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
Now, 50/4 and 59 /4 are like fractions.
50/4 + 59 /4 = 109 / 4
= 27 1/4 Litre
= 27 1/4 Litres of juice did he purchase together in two days.
Alternative Solution,
12 1/52 + 14 3/4
= 25/2 + 59/4
= 50 + 59/4
= 109/4
= 27 1/4 litres
So, he purchase 27 1/4 litres together in two days.
Question no – (117)
Solution :
Nazima gave 2 3/4 litres out of the 5 1/2 litres of juice she purchased to her friends
Total purchased juice = 5 1/2 litres = 5 x 2 + 1 / 2 = 11/2 Litre
She gave to friend = 2 3/4 litres = 2 x 4 + 3/4 = 11/4 Litre.
11/2 Litre – 11/4 Litre.
Here, denominator of both the fractions are different. So, we subtract them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
11/ 2 = 11 x 2 / 2 x 2 = 22 / 4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
11 / 4 = 11 x 1 / 4 x 1 = 11 / 4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
Now, 22/4 and 11 /4 are like fractions.
22/4 – 11 /4
= 11/4
= 2 3/4 Litre.
2 3/4 litres of juice is left with her
Alternative Solution,
5 1/2 – 2 3/4
= 11/2 – 11/4
= 22 – 11/4
= 11/4
= 2 3/4 litres
Thus, 2 3/4 litres of juice is left with her.
Question no – (118)
Solution :
Roma gave a wooden board of length 150 1/4 cm to a carpenter for making a shelf.
In fraction, 150 1/4 cm = 150 x 4 + 1 / 4 = 601 / 4 cm.
The Carpenter sawed off a piece of 40 1/5 cm from it.
In fraction, 40 1/5 cm = 40 x 5 + 1 / 5 = 201 / 5 cm
Length of the remaining piece = 601 / 4 cm. – 201 / 5 cm
Here, denominator of both the fractions are different. So, we subtract them by converting into like fraction.
For this, find LCM of 4 and 5.
LCM of 4 and 5 is 20.
Making denominator of both fractions is 20.
601/ 4 = 601 x 5 / 4 x 5 = 3005 / 20
(Multiplying numerator and denominator by 5, to make the denominator 20.)
201 / 5 = 201 x 4 / 5 x 4 = 804 / 20
(Multiplying numerator and denominator by 4, to make the denominator 20.)
Now, 3005/20 and 804 /20 are like fractions.
3005/20 – 804 /20
= 2201/20
= 110 1/20 cm
Length of the remaining piece is 110 1/20 cm.
Alternative Solution,
(150 1/4 – 40 1/5) cm
= 601/4 – 201/5) cm
= 3005 – 804/20
= 2201/20 ÷ 2201 = 110
= 110 1/20 cm
∴ Length of the remaining piece 110 1/20 cm.
Question no – (119)
Solution :
Nasir travelled 3 1/2 km in a bus.
In fraction, 3 1/2 km = 3 x 2 + 1 / 2= 7/2 km
Walked 1 1/8 km to reach a town.
In fraction, 1 1/8 km = 1 x 8 + 1 / 8 = 9 /8 km.
He travel to reach the town = 7/2 km + 9 /8 km.
Here, denominator of both the fractions are different. So, we add them by converting into like fraction.
For this, find LCM of 2 and 8.
LCM of 2 and 8 is 8.
Making denominator of both fractions is 8.
7/ 2= 7 x 4 / 2 x 4 = 28 / 8
(Multiplying numerator and denominator by 4, to make the denominator 8.)
9 / 8 = 9 x 1 / 8 x 1 = 9 / 8
(Multiplying numerator and denominator by 1, to make the denominator 8.)
Now, 28/8 and 9 /8 are like fractions.
28/8 + 9 /8
= 37 / 8
= 4 5/8 km.
He travel to reach the town is 4 5/8 km.
Alternative Solution,
3 1/2 + 1 1/8
= 7/2 + 8/9
= 28 + 9/8
= 4 5/8
∴ He travel 4 5/8 km to reach the town.
Question no – (120)
Solution :
The fish caught by Neetu was of weight 3 3/4 kg.
In fraction, 3 3/4 kg = 3 x 4 + 3 / 4 = 15 / 4 kg.
The fish caught by Narendra was of weight 2 1/2 kg.
In fraction, 2 1/2 kg = 2 x 2 + 1 / 2 = 5 / 2 kg.
How much more did Neetu’s fish weight than that of Narendra =
We have to subtract 5 / 2 kg. From 15 / 4 kg.
Here, denominator of both the fractions are different. So, we subtract them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
15 / 4 = 15 x 1 / 4 x 1 = 15 / 4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
5/ 2 = 5 x 2 / 2 x 2 = 10 / 4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
Now, 15/4 and 10 /4 are like fractions.
15/4 – 10 /4
= 5/4
= 1 1/4 kg.
Neetu’s fish weight 1 1/4 kg. than that of Narendra.
Alternative Solution,
3 3/4 kg – 2 1/2 kg
= (15/4 – 5/2) kg
= 15 – 10/4
= 5/4 kg
= 1 1/4 kg
Thus, Neetu’s fish weighs 1 1/4 kg more than Narendra.
Question no – (121)
Solution :
Neelam’s father needs 1 3/4 m of cloth for the skirt of Neelam’s new dress.
In fraction. 1 3/4 m = 1 x 4 + 3 / 4 = 7/4 m
And 1/2 m for the scarf.
Cloth must he buy in all = 7/4 m + 1/2 m
Here, denominator of both the fractions are different. So, we add them by converting into like fraction.
For this, find LCM of 2 and 4.
LCM of 2 and 4 is 4.
Making denominator of both fractions is 4.
7 / 4 = 7 x 1 / 4 x 1 = 7 / 4
(Multiplying numerator and denominator by 1, to make the denominator 4.)
1/ 2 = 1 x 2 / 2 x 2 = 2 / 4
(Multiplying numerator and denominator by 2, to make the denominator 4.)
Now,
7/4 and 2 /4 are like fractions.
7/4 + 2 /4
= 9 / 4
= 2 1/4 m
Cloth must he buy in all is 2 1/4 m
Alternative Solution,
(1 3/4 + 1/2)
= 7/4 + 1/2
= 7 + 2/4
= 9/4
= 2 1/4 m
∴ 2 1/4 Cloth he must buy.
Question no – (122)
Solution :
Equation – (a)
8 1/2 = 8 2/4
+ 4 1/4 = 4 1/4
—————————
= 12 3/8
Equation – (b)
6 1/2
+ 2 1/4
—————————
= 8 2/6 = 8 1/3
Question no – (123)
Solution :
1 metre 40 centimetres + 60 centimetres
We know, 100 cm = 1 metre
1 metre 40 centimetres = 140 cm
1 metre 40 centimetres + 60 centimetres = 140 + 60 = 200 cm
200 cm = 2 metre.
2 metre < 2.6 metres.
Alternative Solution,
1 metre 40 cm
+ 60 cm
———————–
1 metre 100 cm = 2 metre
∴ 2.6 metres is greater.
Question no – (125)
Solution :
0 is the whole number.
0, 1, 2, 3, 4, 5. = There are total 6 numbers out of 5 are natural numbers.
Fraction that represents the number of natural numbers to total numbers in the collection =
Total natural number / Total numbers = 5 / 6.
(ii) Fraction that represents the number of whole numbers to total numbers in the collection
= Total whole number / Total numbers
= 6 / 6
= 1
Question no – (126)
Solution :
Numbers – 3, – 2, – 1, 0, 1, 2, 3
Total 7 numbers out of which 3 are natural numbers (1, 2, 3)
(i) Fraction representing the total number of natural numbers in the collection of numbers
Total natural number / Total numbers = 3 / 7
(ii) Total whole numbers are 4 (0, 1, 2, and 3)
Fraction representing the total number of whole numbers in the collection of numbers
Total whole number / Total numbers = 4 / 7
(iii) All numbers are integers.i.e.7
Fraction representing the total number of integers in the collection of numbers =
Total integers / Total numbers = 7/ 7
Question no – (127)
Solution :
Let X be the first term.
Let Y be the Second term.
X + Y = 7/11 ——- (i) and X – Y = 2/11. ———– (ii)
Adding equation 1 and 2, we get,
2 x X = 7/11 + 2/11
2 x X = 9/11
X = 9/11 x 2 = 9 /22
The first term is X = 9/22
We put this value in equation 1.
X + Y = 7/11 ——- (i)
9/22 + Y = 7/11
Y = 7/11 – 9/22
We make denominator 22
7/11 multiply this by 2 we get,
7 x 2/11 x 2 = 14 / 22
Y =14 / 22 – 9/22
Y = 5/22
9 /22 and 5/ 22 are the pair of fractions.
Alternative Solution,
Let, the fractions be x, y
x + y = 7/11
+ x – y = 2/11
——————————–
2x = 7/11 + 2/11
= 2x = 9/11
∴ X = 9/22
Y = 7/11 – 9/22
= 14 – 9/22
= 5/22
∴ Pair of a fractions 9/22 and 5/22
Question no – (128)
Solution :
Straight angle having measure 180°
Right angle having measure 90°
Fraction of a straight angle is a right angle
= 90°/180°
= 1/2
Alternative Solution,
= 90 °/180 °
= 1/2
∴ Fractions of a straight angle is right angle.
Question no – (129)
Solution :
| Cards : | Bags : |
| (i) 3/7 | < 1 – Bag I |
| (ii) 4/4 | = 1 – Bag – II |
| (iii) 9/8 | > 1 – Bag – III |
| (iv) 8/9 | < 1 – Bag I |
| (v) 5/6 | < 1 – Bag I |
| (vi) 6/11 | < 1 – Bag I |
| (vii) 18/18 | = 1 – Bag – II |
| (viii) 19/25 | < 1 – Bag I |
| (ix) 2/3 | < 1 Bag I |
| (x) 13/17 | < 1 – Bag I |
Next Chapter Solution :