Maths Wiz Solutions Class 7 Chapter 3 Playing with Numbers
Welcome to NCTB Solutions. Here with this post we are going to help 7th class students for the Solutions of Maths Wiz Class 7 Math Book, Chapter 3, Playing with Numbers. Here students can easily find step by step solutions of all the problems for Playing with Numbers, Self Practice 3A, 3B, 3C, 3D, 3E, 3F, 3G, 3H, 3I and 3J Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 3 solutions. Here in this post all the solutions are based on ICSE latest Syllabus.
Playing with Numbers Self Practice 3A Solution :
Question no – (1)
Solution :
(a) All the Factors of 12,
= 1 × 12
= 2 × 6
= 3 × 4
∴ 1, 12, 2, 3, 6, 4
So, all the factors of 12 is 1, 12, 2, 3, 6, 4
(b) All the factors of 14
= 2 × 7
= 1 × 14
= 1, 2, 7, 14
Thus, al the factors of 14 are 1, 2, 7, 14.
(c) Factors of 19
= 1 × 9
∴ 1, 9
Hence, all the factors of 19 is 1, 9
(d) Factor of 21
= 1 × 21
= 3 × 7
∴ 3, 7
Therefore, all the factors of 21 is 3, 7
(e) Factors of 24
= 1 × 24
= 2 × 12
= 3 × 8
= 4 × 6
∴ 1, 2, 3, 4, 6, 8, 12, 24,
Thus, all the factors of 24 is 1, 2, 3, 4, 6, 8, 12, 24.
(f) Factors of 23
= 1 × 23
∴ 1, 2, 3
Hence, all the factors of 23 is 1, 2, 3.
(g) Factors of 42
= 1 × 42
= 2 × 24
= 3 × 14
= 6 × 7
∴ 1, 2, 3, 6, 7, 14, 24, 42
Thus, all the factors of 42 is 1, 2, 3, 6, 7, 14, 24, 42
(h) Factors of 85
= 1 × 85
= 5 × 17
∴ 1, 5, 17, 85
So, all the factors of 85 is 1, 5, 17, 85
(i) Factors of 73
= 1 × 73
∴ 1, 73
So, all the factors of 73 is 1, 73
(j) Factors of 92
= 1 × 92
= 2 × 46
= 4 × 23
∴ 1, 2, 4, 23, 46, 92
Therefore, all the factors of 92 is 1, 2, 4, 23, 46, 92.
Question no – (2)
Solution :
(a) The first 5 multiples of 2 are 2, 4, 6, 8, 10
(b) The first 5 multiples of 4 are 4, 8, 12, 16, 20
(c) The first 5 multiples of 6 are 6, 12, 18, 24, 30
(d) The first 5 multiples of 9 are 9, 18, 27, 36, 45
(e) The first 5 multiples of 10 are 10, 20, 30, 40, 50
Question no – (3)
Solution :
The multiples of 7 between 1 and 75 are
1 × 7 = 7
2 × 7 = 14
3 × 7 = 21
4 × 7 = 28
5 × 7 = 35
6 × 7 = 42
7 × 7 = 49
7 × 8 = 56
7 × 9 = 63
7 × 10 = 70
Question no – (4)
Solution :
The multiples of 9 upto 100
Multiples of 9 = 9 × 1, 9 × 2, 9 × 3, 9 × 4, 9 × 5 , 9 × 6 ,9 ×7 ,9 × 8, 9 × 9 ,9 × 10 , 9 × 11.
Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99
Question no – (5)
Solution :
(a) The ninth multiple of 75 is 675
= 75 × 9
= 675
(b) The multiples of 10 between 150 and 200 are –
15 × 10 = 150
16 × 10 = 160
17 × 10 = 170
180 × 10 = 180
19 × 10 = 190
20 × 10 = 200
Question no – (6)
Solution :
Addition Facts :
Addition = (E).
Example : 2 + 8 = 10
Odd + Odd = (E).
Example : 3 + 5 = 8
Even + Odd = (o).
Example : 6 + 5 = 11
Multiplication Facts :
Even × Even = (E)
Example : 2 × 6 = 12
Odd × Odd = (E)
Example : 7 × 9 = 63
Even × Odd = (O)
Example : 8 × 3 = 2
Playing with Numbers Self Practice 3C Solution :
Question no – (1)
Solution :
(a) 35 = Composite
(b) 29 = Prime
(c) 23 = Prime
(d) 57 = Composite
(e) 61 = Prime
(f) 19 = Prime
(g) 63 = Composite
(h) 93 = Composite
(i) 102 = Composite
(j) 89 = Prime
(k) 99 = Composite
(l) 48 = Composite
(m) 79 = Prime
(n) 53 = Prime
(o) 105 = Composite
(p) 47 = Prime
(q) 83 = Prime
Question no – (2)
Solution :
(a) Prime and Composite numbers less than 20.
| Prime : | Composite : |
| 2 | 4 |
| 3 | 6 |
| 7 | 8 |
| 5 | 9 |
| 11 | 10 |
| 13 | 12 |
| 17 | 14 |
| 19 | 15 |
| 16 | |
| 18 |
(b) The largest prime number between 1 and 10 is 7
(c) 7 consecutive numbers, none of which is prime 90, 91, 92, 93, 94, 95, 96
Question no – (3)
Solution :
Here, the pair of co-primes are,
(b) 18 and 35
= Co-primes
(c) 56 and 45
= Co-primes
Question no – (4)
Solution :
The pair of twin primes are,
(b) 5, 7
= Twin primes
(c) 59, 61
= Twin primes
Playing with Numbers Self Practice 3D Solution :
Question no – (1)
Solution :
(a) 12 as the sum of two primes
= 5 + 7
= 12
(b) 30 as the sum of two primes
= 11 + 19
= 30
(c) 68 as the sum of two primes
= 31 + 37
= 68
(d) 72 as the sum of two primes
= 31 + 41
= 72
Question no – (2)
Solution :
(a) 12 as sum of two odd primes
= 5 + 7
= 12
(b) 30 as sum of two odd primes
= 13 + 17
= 30
(c) 78 as sum of two odd primes
= 37 + 41
= 78
(d) 90 as sum of two odd primes
= 47 + 53
= 90
Question no – (3)
Solution :
(a) 15 as sum of three odd primes
= 3 + 5 + 7
= 15
(b) 23 as sum of three odd primes
= 5 + 11 + 7
= 23
(c) 35 as sum of three odd primes
= 5 + 7 + 23
= 35
(d) 55 as sum of three odd primes
= 13 + 19 + 23
= 55
Question no – (4)
Solution :
The five pairs of prime numbers are,
(i) 2, 13)
(ii) (3, 17)
(iii) (3, 7)
(iv) (2, 3)
(v) (13, 17)
Question no – (5)
Solution :
(a) Given number, 151
= Yes, it is a prime number.
(b) 69
= No, it is not a prime number.
(c) 241
= Yes, it is a prime number.
(d) 265
= No, it is not a prime number.
Question no – (6)
Solution :
Given number, 385
= 5 × 7 × 11
Therefore, the three prime numbers are 5, 7, and 11.
Question no – (7)
Solution :
If two numbers are co-prime, at least one of the must be prime
This statement is False.
Playing with Numbers Self Practice 3E Solution :
Question no – (1)
Solution :
(a) 24
∴ 24 = 2 × 2 × 2 × 3
(b) 36
∴ 36 = 2 × 2 × 3 × 3
(c) 210
∴ 210 = 3 × 7 × 5 × 2
(d) 180
∴ 180 = 2 × 3 × 3 × 2 × 5
For more better understanding :

Question no – (2)
Solution :
(a) Given number, 32
∴ 32 = 2 × 2 × 2 × 2 × 2
= 25
(b) 48
∴ 48 = 2 × 2 × 2 × 2 × 3
= 22 × 3
(c) 66
∴ 66 = 2 × 3 × 11
= 66
(e) 84
∴ 84 = 2 × 2 × 3 × 7
= 22 × 3 × 7
(f) 100
∴ 100 = 2 × 2 × 5 × 5
= 22 × 52
(g) 840
∴ 840 = 2³ × 3 × 5 × 7
(h) 504
∴ 504 = 2 ×2 × 2 × 3 × 3 × 7
= 23 × 32 × 7
(i) 2904
∴ 2904 = 2 × 2 × 2 × 3 × 11 × 11
= 23 × 3 × 112
(j) 19845
∴ 19845 = 3 × 3 × 3 × 5 × 7 × 7
= 33 × 5 × 72
Question no – (3)
Solution :
Prime factorisation of 343
∴ 343 = 7 × 7 × 7
= 73
Therefore, the Prime factorisation of 343 will be 73
Question no – (4)
Solution :
(a) When all the factors are prime and their product is the origin.
(b) Prime factor of a number are all prime number where factor of a number don’t have to be prime.
Playing with Numbers Self Practice 3F Solution :
Question no – (1)
Solution :
(a) 18, 27
HCF of 18, 27

∴ HCF = 3 × 3 = 9
∴ HCF of 18, 27 is 9
(b) 32, 72
HCF of 32, 72

∴ HCF = 2 × 2 × 2 = 8
Therefore, HCF of 32, 72 is 8
(c) 60, 84
HCF 60, 84

∴ HCF = 2 × 2 × 3 = 12
Thus, HCF of 60, 84 is 12.
(d) 44, 66
HCF of 44, 66

∴ HCF = 12 × 2 = 22
Hence, the HCF of 44, 66 is 22.
(e) 80, 112
HCF of 80, 112

∴ HCF = 2 × 2 × 2 × 2
= 16
Hence, HCF of 80, 112 is 16
(f) 21, 306
HCF of 21, 306

∴ HCF = 3
Thus, HCF of 21, 306 will be 3.
(g) 28, 70
HCF of 28, 70

∴ HCF = 2 × 7 = 14
Thus, the HCF of 28, 70 is 14.
(h) 35, 105
HCF of 35, 105

∴ HCF = 5 × 7 = 35
Therefore, the HCF of 35, 105 is 35.
Question no – (2)
Solution :
(a) Given number, 16, 24, 40
HCF of 16, 24, 40

∴ HCF = 2 × 2 × 2 = 8
Thus, the HCF of 16, 24, 40 is 8
(b) 28, 35, 49
HCF of 28, 35, 49

∴ HCF = 7
Hence, the HCF of 28, 35, 49 is 7.
(c) 15, 30, 60
HCF of 15, 30, 60

∴ HCF = 5 × 3 × 2 = 30
Thus, the HCF of 15, 30, 60 is 30.
(d) 75, 225, 150
HCF of 75, 225, 150

∴ HCF = 25 × 3 = 75
Hence, the HCF of 75, 225, 150 is 75.
Question no – (3)
Solution :
(a) Given number, 198, 342
HCF of 198, 342 by long division method

∴ HCF = 18
Thus, the HCF of 198, 342 is 18.
(b) 345, 506
HCF of 345, 506 by long division method

∴ HCF = 23
Hence, the of 345, 506 is 23.
(c) 325, 390, 455
HCF of 325, 390, 455 by long division method

∴ HCF = 65
So, the HCF of 325, 390, 455 is 65.
(d) 318, 848, 689
HCF of 318, 848, 689 by long division method

∴ HCF = 4
Therefore, HCF of 318, 848, 689 is 4.
Question no – (4)
Solution :
(a) Two consecutive natural numbers = 2, 3
∴ HCF of 2, 3 = 1
(b) Two consecutive even numbers = 6, 8
∴ HCF of 6, 8
= 2 ÷ 6 = 3
= 2 ÷ 8 = 4
∴ HCF = 2
(c) Two consecutive odd numbers = 5, 7
∴ HCF of 5, 7
= 5 ÷ 1 = 5
= 7 ÷ 1 = 7
∴ HCF of 5, 7 is = 1
Playing with Numbers Self Practice 3G Solution :
Question no – (1)
Solution :
HCF of 30, 24, 12 = 12

∴ HCF = 2 × 3 = 6
∴ Max number of basket = 6
Therefore, the the maximum number of 6 baskets Karishma will make.
Question no – (2)
Solution :
HCF of 27, 45, 99, 117

∴ HCF = 3 × 3 = 9
Therefore, the number of row in garden will be 9
Question no – (3)
Solution :
Remainder 2 in both case
∴ (110 – 2) = 108
And (128 – 2) = 126
∴ HCF of 108 and 126

∴ HCF = 2 × 9 = 18
Hence, the greatest number is 18.
Question no – (4)
Solution :
Remainder 3 for 307
∴ (307 – 7) = 304
Remainder 3 for 330
∴ (330 – 7) = 323
∴ HCF of 304 and 323

∴ HCF = 19
Therefore, the required greatest number is 19.
Question no – (5)
Solution :
HCF of 40, 32

∴ HCF = 2 × 2 × 2 = 8
∴ No of team = 8
∴ No of boys in each team = 40/8 = 5 boys
∴ No of boys in each team = 32/8 = 4 girls
Therefore, the number girls are 4 and boy’s are 5
Question no – (6)
Solution :
First, 8 m 25 cm
= (8 × 100 + 25)
= 825 cm
Second, 6 m 75 cm
= (6 × 100 + 75)
= 75 cm
Third, 4 m 50 cm
= (4 × 100 + 50)
= 450 cm
HCF of 825, 675, 450

∴ HCF = 75
Therefore, the required longest tap will be 75 cm
Question no – (7)
Solution :
Length = 20 m 16 cm
= (20 × 100 + 16)
= 2016
Breadth = 15 m 60 cm
= (15 × 100 + 60)
= 1560 cm
∴ HCF of 2016 and 1560

∴ HCF = 24
∴ No of stone,
= 2016 × 156/ 24 × 24
= 5460
Therefore, the least possible number of such stones 5460.
Question no – (8)
Solution :
Remainder 11
= (3026 – 11)
= 3015
Remainder 13
= (5053 – 13)
= 5040
∴ HCF of 3015 and 5040

∴ HCF = 45
Therefore, required greatest number is 45.
Question no – (9)
Solution :
First, HCF of 24, 36, 60

∴ HCF = 12
∴ Number of row,
= 24/12 + 36/2 + 60/12
= 2 + 3 + 5
= 10
Hence, 10 rows are required to arrange the fruits.
Playing with Numbers Self Practice 3H Solution :
Question no – (1)
Solution :
(a) Given, Multiples of 2 = 2, 4, 6, 8,
Multiples of 3 = 3, 6, 9, 12
∴ LCM of 2 and 3
= 2 × 3
= 6
Therefore, the LCM of 2 and 3 = 6
(b) As per the given question,
6 = 2 × 3
10 = 2 × 5
∴ LCM of 6 and 10
= 2 × 3 × 2 × 5
= 2 × 3 × 5
= 30
(c) Given in the question,
9 = 3³
15 = 3 × 5
∴ LCM of 9 and 15,
= 32 × 3 × 5
= 3 × 3 × 5
= 45
(d) Given, 4 = 2²
14 = 2 × 7
∴ LCM of 4 and 14,
= 2 × 2 × 2 × 7
= 2 × 2 × 7
= 28
(e) Given, 12 = 2² × 3
32 = 2⁵
∴ LCM of 12 and 32,
= 2 × 2 × 3 × 25
= 2 × 3 × 2 × 2 × 2 × 2
= 96
(f) As per the question,
25 = 5²
100 = 5² × 2²
LCM of 25 and 100,
= 2 × 2 × 52 × 52 ×
= 2 × 52
= 50
Question no – (2)
Solution :
(a) Given number, 7 and 14
∴ LCM of 7, 14,
= 7 × 7 × 2
= 7 × 2
= 14
Therefore, the LCM of 7 and 14 is 14.
(b) 5 and 7
∴ LCM of 5 and 7,
= 5 × 7
= 35
Thus, the LCM of 5 and 7 is 35.
(c) 13 and 26
∴ LCM of 13, 26 ,
= 13 × 13 × 2
= 13 × 2
= 26
Hence, the LCM of 13 and 26 is 26.
(d) 4 and 5
∴ LCM of 4, 5,
= 4 × 5
= 20
So, the LCM of 4 and 5 is 20.
(e) 4 and 10
∴ LCM of 4, 10,
= 2 × 2 × 2 × 5
= 2 × 2 × 5
= 20
Thus, the LCM of 4 and 10 is 20.
(f) 6 and 14
∴ LCM of 6, 14,
= 2 × 3 × 2 × 7
= 2 × 3 × 7
= 42
So, the LCM of 6 and 14 is 42.
(g) 25 and 20
∴ LCM of 25 and 20 ,
= 5 × 5 × 5 × 4
= 5 × 5 × 4
= 100
Therefore, the LCM of 25 and 20 is 100.
(h) 27 and 72
∴ LCM of 27 and 72,
= 3 × 9 × 9 × 8
= 9 × 3 × 8
= 216
Thus, the LCM of 27 and 72 is 216.
(i) 14 and 35
∴ LCM of 14 and 35,
= 2 × 7 × 7 × 5
= 2 × 5 × 7
= 70
Therefore, the LCM of 14 and 35 is 70.
(j) 24 and 30
∴ LCM of 24 and 30,
= 2 × 2 × 2 × 3 × 3 × 2 × 5
= 5 × 3 × 2 × 2
= 60
Therefore, the LCM of 24 and 30 is 60.
(k) 64 and 80
∴ LCM of 64 and 80,
= 26 × 24 × 5
= 5 × 25
= 320
Therefore, the LCM of 64 and 80 is 320.
(l) 81 and 108
∴ LCM of 81 and 108,
= 9 × 9 × 2 × 2 × 3 × 9
= 2 × 3 × 9 × 9
= 324
Therefore, the LCM of 81 and 108 is 324.
(m) 4, 8 and 10
∴ LCM of 4, 8 and 10,
= 2 × 2 × 2 × 2 × 2 ×2 × 5
= 2 × 2 × 2 × 5
= 40
Thus, the LCM of 4, 8 and 10 is 40.
(n) 4, 5 and 7
∴ LCM of 4, 5 and 7,
= 4 × 2 × 5 × 7
= 140
Thus, the LCM of 4, 5 and 7 is 14.
(o) 2, 4, 5 and 6
∴ LCM of 2, 4, 5 and 6
= 2 × 2 × 2 × 5 × 2 × 3
= 2 × 2 × 15
= 60
Therefore, the LCM of 2, 4, 5 and 6 is 60.
(p) 4, 8, 16 and 64
∴ LCM of 4, 8, 16 and 64,
= 2 × 2 × 2 × 2 × 3 × 2 × 2 × 2 × 2 × 2 × 26
= 64
Therefore, the LCM of 4, 8, 16 and 64 is 64.
Question no – (3)
Solution :
(a) 12, 16 and 18
∴ LCM of 12, 16, 18,

∴ LCM = 2 × 2 × 3 × 4
= 144
Thus, the LCM of 12, 16 and 18 is 144.
(b) 7, 21 and 28
∴ LCM of 7, 21 and 28,

∴ LCM = 7 × 3 × 4
= 84
So, the LCM of 7, 21 and 28 is 84
(c) 30, 42 and 63
∴ LCM of 30, 42 and 63

∴ LCM = 3 × 2 × 7 × 5 × 3
= 630
So, the LCM of 30, 42 and 63 is 630.
(d) 72, 96 and 120
∴ LCM of 72, 96 and 120

∴ LCM = 2 × 2 × 3 × 2 × 3 × 4 × 5
= 1440
Hence, the LCM of 72, 96 and 120 is 1440.
(e) 240, 300, 600
∴ LCM of 240, 300, 600

∴ LCM = 2 × 5 × 3 × 2 × 2 × 5 × 2
= 1200
So, the LCM of 240, 300, 600 is 1200
(f) 15, 20, 28 and 35
∴ LCM of 15, 20, 28 and 35

∴ LCM = 5 × 4 × 7 × 3
= 420
Therefore, the LCM of 15, 20, 28 and 35 is 420
Question no – (4)
Solution :
(a) Greatest number will be LCM.
Example :
LCM of 2, 4,
= 2 × 2 × 2 = 2 × 2
= 4
(b) Then they are co-prime number.
Example :
= LCM of 2 and 5
= 2 × 5
= 10
(d) No, never smaller in the any number of group.
Example :
= LCM of 2, 4, 8 = 2 × 2 × 2 × 2 × 2 × 2
= 2 × 2 × 2
= 8
(e) Difference of LCM and GCF
LCM is least common multiple.
GCF is greatest common factor.
Playing with Numbers Self Practice 3I Solution :
Question no – (1)
Solution :
LCM of 6 and 7 = 42
Least number of member = 42
The least number of members the team can have is 7.
Question no – (2)
Solution :
LCM of 6, 8, 10
= 2 × 3 × 2 × 2 × 2 × 2 × 5
= 2 × 2 × 2 × 3 × 5
= 120
Thus, the minimum number of students will be 120.
Question no – (3)
Solution :
= LCM of 200, 300, 3600, 450
= 2 × 100 × 3 × 100 × 3 × 3 × 2 × 2 × 100 × 5 × 3 × 3 × 100
= 1800 s
Therefore, They meet at the starting point for the first time in 1800 s.
Question no – (4)
Solution :
LCM of 24, 36, 54,

∴ LCM = 2 × 3 × 2 × 3 × 2 × 3
= 216s
∴ Lights will change after 2165
= 246/60
= 3m 36 s
∴ If they change 1st,
= 10 : 15 : 00 AM
∴ If they change next
= (10 : 15: 00 + 00 : 03 : 36)
= 10 : 18 : 36 AM
Question no – (5)
Solution :
LCM of 21, 36, 66,

∴ LCM = 3 × 2 × 7× 6 × 11
= 2772
∴ Least perfect square = (2772)2
Question no – (6)
Solution :
LCM of 24, 32, 36, 54,
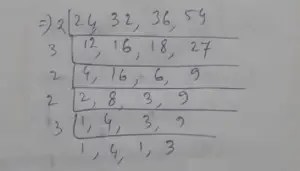
∴ LCM = 2 × 2 × 3 × 2 × 2 × 3 × 4
= 856
∴ Increase by ‘5’
∴ The least number,
= 856 + 5
= 859
Therefore, the required smallest number will be 859
Playing with Numbers Self Practice 3J Solution :
Question no – (1)
Solution :
| S. No. | Column 1 | Column 2 |
| Product of Numbers | Product of HCF and LCM | |
| (a) | 9 × 12 = 108 | 3 × 36 = 108 |
| (b) | 15 × 20 = 300 | 5 × 60 × 30 |
| (c) | 21 × 24 = 504 | 168 × 3 = 504 |
| (d) | 20 × x = 240 | 60 × 4 = 240 |
(b) HCF of 15and 20 = 5
LCF of 15 and 20 = 3 × 5, 4 × 5
= 3 × 4 × 5
= 60
∴ Column 2 = 5 × 60 = 3 0
(c) 21 × 24 = 504
HCF of 21 and 24 = 3
LCF of 21 and 24 = 3 × 7 3 × 8,
= 3 × 8 × 7
= 186
∴ Column 2 = 168 × 3 = 504
(d) 20 × x × 20
or, x = 240/20 = 12
∴ 20 × 12 = 240
HCF of 20 and 12 = 4
LCM of 20 and 12 = 4 × 5, 3 × 4
= 4 × 5 × 3
= 60
∴ Column 2 = 60 × 4 = 240
Question no – (2)
Solution :
As per the question,
LCM of two numbers = 1820
HCF = 26
one number = 130
Other number = ?
Let, the another number = x
We now x × 130 = 1820 × 26
or, x = 1820 × 26/130
= 364
Therefore, the other number will be 364.
Question no – (3)
Solution :
No, 570 in not exactly divisible by 14.
Question no – (4)
Solution :
HCF of P, Q,
= 23 × 310 × 5, 25 × 3 × 7
= 23 × 3
LCM of P, Q,
= 23 × 310 × 5, 25 × 3 × 7
= 25 × 310 × 5 × 7
Question no – (5)
Solution :
The appropriate option is – (d) 80
(c) 72 can’t be divisible by 6,
So they never can be LCM.
Next Chapter Solution :
👉 Chapter 4 👈