Warning: Undefined array key "https://nctbsolution.com/joy-of-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Joy of Mathematics Class 8 Solutions for Chapter 1 Operations on Sets
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Joy of Mathematics Class 8 Book, Chapter 1 Operations on Sets. Here students can easily find step by step solutions of all the problems for Operations on Sets. Exercise wise proper solutions for every problems. All the problem are solved with easily understandable methods so that all the students can understand easily. Here students will find solutions for Exercise 1.1, 1.2, 1.3 and 1.4
Operations on Sets Exercise 1.1 Solution :
Question no – (1)
Solution :
(a) Yes, It is a set
Let, the set is R
R = {V, I, B, G, O, Y, R}
(b) Yes, It is a set
(c) No, It is not a set
(d) No, It is not a well-defined description
So, it, is not a set
(e) No, it is not a set
(f) Yes, It is a set
Let, the set is A = {All natural numbers lying between 3 and 4}
Question no – (2)
Solution :
(a) A = {A, L, H, B, D}
(b) B = {I, N, D, A,}
(c) C = {L, O, N, D}
(d) D = {K, O, L, A, T}
(e) E = {A, M, R, I, T, S, R}
Question No – (3)
Solution :
A = {Prime numbers less than 20}
A = {2, 3, 5, 7, 11, 13, 17, 19}
(a) 2 ∈ A
(b) 20 ∉ A
(c) 9 ∉ A
(d) 3 ∈ A
(e) 11 ∈ A
(f) 19 ∈ A
Question no – (4)
Solution :
(a) A = {Values of the English alphabet}
(b) B = {Squares of natural numbers less than 5}
(c) C = {First five multiple of 5}
(d) D = {Months with exactly 30 days}
(e) E = {odd prime numbers less than 15}
(f) F = {Whole numbers less than 5}
Question no – (5)
Solution :
(a) A = {x : x = 3n, n ∈ w and n < 4}
= A = {0, 3, 6, 9}
(b) B = {6/13, 7/15, 8/17…. }
(c) C = {3}
(d) D = {- 3, – 2, – 1, 0, 1, 2, 3,}
(e) E = {1, 2, 3, 4, 5, 6, 9, 12, 18, 36}
(f) F = {1/7, 2/9, 8/11, 4/13, 5/15}
Question no – (6)
Solution :
(a) A = {x : x ∈ N}
(b) B = {x : x= 2x + 1; n ∈ W and n < 5}
(c) C = {x : x = 2n, n ∈ Z)
(d) D = {x : x is a factor of 15}
(e) E = {x : x – n3 , n ∈ N and n ≤ 7}
(f) F = {x : x = 2x – 1/2x + 1, n ∈ N}
Operations on Sets Exercise 1.2 Solution :
Question no – (1)
Solution :
(a) The cardinal number of sets A is n (A) = 5
(b) B = {x : x ∈ N and 2 < x < 7}
= {3, 4, 5, 6}
n(B) = 4
(c) C = {x : x ∈ W and 3x – 2 ≤ 7}
If x = 1
= 3 × 1 – 2 ≤ 7
= 1 ≤ 7
= x = 2
= 3 × 2 – 2 ≤ 7
= 4 ≤ 7
Let, x = 3
= 3 × 3 – 2 ≤ 7
= 7 ≤ 7
= C = {1, 2, 3}
n(c) = 3
(d) D = {x : x ∈ N and x ≤ 5}
= D = {1, 2, 3, 4, 5}
= n(D) = 5
(e) E {x : x ∈ Z and 3 ∠x ∠ 4}
= n(E) = 0
(f) F = {3}
= n(F) = 1
(g) G = {x : x is a letter in the word VISAKHAPATNAM}
= {V, I, S, A, K, H, P, T, N, M}
= n(G) = 10
Question no – (2)
Solution :
(a) {x : x ∈ Z and x < 10}
= {x : 1, 2, 3, 4, 5, 6, 7, 8, 9}
∴ The set is finite.
(b) {x = 4/3n, n ∈ W and 0 < n < 10}
x = 4/3 × 1 = 4/3, 4/3 × 2 = 4/6, 4/3 × 3 = 4/9
= 4/3 × 4 = 4/12, 4/3 × 5 = 4/15, 4/3 × 6 = 4/18, 4/3 × 7 = 4/21
= 4/3 × 8 = 4/24, 4/3 × 9 = 4/27
= {4/3, 4/6, 4/9, 4/12, 4/15, 4/18, 4/21, 4/24, 4/27}
∴ It is a finite set
(c) {x : x ∈ N and x > 11}
∴ It is an Infinite set
(d) {x : x ∈ N and 10 ≤ x ≤ 11}
= {10, 11}
∴ It is an finite set.
(e) {x : x is a letter in word BOOSTER}
= {B, O, S, T, E, R}
∴ It is a finite set.
Question no – (3)
Solution :
(a) {x : x ∈ N and 5 < x < 6}
There is no natural number between 5 and 6
∴ So, this an empty set
(b) There is no prime number between 13 and 17
∴ Hence It is an empty set.
(c) {x : x is a prime and 13 ≤ x ≤ 17}
= {13, 17}
It is not a empty set because It has two elements.
(d) [x : x2 + 9 = 0 and x ∈ N}
It is an empty set as there is no natural number whose square is negative
(e) {x : x ∈ W and 5 ≤ x ≤ 7}
= {5, 6, 7}
It is a non empty set because it a clement 5, 6, 7.
(f) {Vowels in the word GYM}
There is no vowel in the word GYM So, It is an empty set.
Question no – (4)
Solution :
(a) True
(b) False
Question no – (5)
Solution :
(a) A = {x : x ≤ 5 and x ∈ W}
B = {0, 1, 2, 3, 4}
A = {1, 2, 3, 4, 5}
n(A) = 5
n(B) = 5
∴ n(A) = n(B)
Therefore A is equivalent to B (A ⇿ B)
(b) A = {x : x is a letter of the word BHOPAL}
= {B, H, O, P, A, L,}
B = {6, 5, 1, 2, 3, 4}
n(A) = 6
n(B) = 6
∴ n(A) = n(B) = 6
∴ Therefore A is Equivalent to B (A ⇿ B)
(c) A = {x : = 3x, n ∈, w, 0 ≤ n ≤ 3}
= {(3 × 0), (3 × 1), (3 × 2), (3 × 3)}
= {0, 3, 6, 9}
B = {monthly having 31 days}
= {January, March may, July, August, October, December}
n(A) = 4,
n(B) = 7
n(A) ≠ n(B)
Therefore the set A and B is not equivalent set.
(d) A {x : x = 2x + 1, n ∈ N, n < 5}
= {(2 × 1 + 1), (2 × 2 + 1), (2 × 3 + 1), (2 × 4 + 1)}
= {3, 5, 7, 9}
B = {3, 5, 7, 9}
∴ n(A) = 4
n(B) = 4
∴ n(A) = n(B) = 4
∴ Therefore the set A and B is not equivalent set.
Question no – (6)
Solution :
(a) A = {x | 2x2 + 8 = 0, x ∈ N}
∴ There is not only one element in this set
So, It is not a singleton set
(b) B = {Vowels in word CUP}
B = {U}
∴ there is only one element in this set.
So, this is a singleton set.
(c) C = {x | x ∈ N and 3 < x < 5}
= {4}
∴ There is only one element in this set.
So, this is a singleton set.
(d) D = {factors of 37}
= {1, 37}
∴ there is two elements in this set.
So, this is not singleton set.
Question no – (7)
Solution :
(a) A = {Prime numbers lying between 10 and 20}
= {11, 143, 17, 19}
B = {odd prime numbers}
= {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 … }
∴ Set and set B have four common elements
Thus are 11, 13, 17, 19,
Hence set A and B are overlapping set.
(b) A = {common factors of 36 and 45}
= {1, 3, 9}
B = [Multiples of 7}
= {7, 14, 21, 28, …}
Set A and set B have no element in common
∴ Hence A and B are disjoint.
(c) A {First five consecutive natural numbers}
= {1, 2, 3, 4,5}
B = {Integers lying between 3/5 and 7}
Set A and set B five common elements.
Hence, they are overlapping sets.
Question no – (8)
Solution :
(a) U { x | x is a quadrilateral}
(b) U = {x | x ∈ w}
(c) U = {x | x ∈ N, x ≤ 100}
Question no – (9)
Solution :
U = {natural number less than 50}
= {1, 2, 3, 4, …. 50}
B = {multiples of 3 less than 50}
= {3, 6, 9, 12, 15, 21, 24, 27, 10, 33, 36, 39,}
C = {x | x + 7 ≤ 8}
(a) B = {x | x ∈ N and x is not a multiple of 3, x < 50}
(b) C = {x | x ∈ N and 1 < x < 50}
(c) N
(d) n(c)
Operations on Sets Exercise 1.3 Solution
Question no – (1)
Solution :
A = {4, 5, 6}
B= {x : x ∈ W and x < 5}
= {0, 1, 2, 3, 4}
(a) A ∪ B
= {4, 5, 6} ∪ {1, 2, 3, 4}
= {0, 1, 2, 3, 4, 5, 6}
(b) A ∩ B
= {4, 5, 6} ∩ {0,. 1, 2, 3, 5,}
= {4}
(c) A – B
= {x : x ∈ A, x ∉ B}
= {5, 6}
(d) B – A
= {x : x ∉ B, x ∉ A}
= {0, 1, 2, 3}
Question no – (2)
Solution :
A = {letters of the word NEW JERSEY}
= {N, E, W, J, R, Y, S}
B = {letters of the word NEW YOURK}
= {N, E, W, Y, O, R, K}
(a) A ∪ B
= {N, E, W, J, R, S, Y} ∪ {N, E, W, Y, O, U, R, K}
= {N, E, W, J, R, S, Y, K, O}
(b) A ∩ B
= {N, E, W, J, E, R, S, Y} ∩ {N E, W, Y, O, R, K}
= {N, E, W, R}
(c) A – B
= {x : x ∈ A, x ∉ B}
= {J, S}
(d) B – A
= {x : x ∈ B, x ∉ A}
= {O, K}
Question no – (3)
Solution :
U = {x : x is a whole number ≤ 9]
= {0, 1, 2, 4, 5, 6, 7, 8, 9}
A = {odd number}
= {1, 3, 5, 7, 9}
B = {multiples of 3}
= {3, 6, 9}
C = {factors of 18}
= {1, 2, 3, 6, 9}
(a) A ∪ B
= {1, 3, 5, 7,9} ∪ {3, 6, 9}
= {1, 3, 5, 7, 9, 6}
(b) B ∪ C
= {3, 6, 9} ∪ {1, 2, 3, 6, 9}
= {1, 2, 3, 6, 9}
(c) (A ∪ B) ∩ (B ∪ C)
= {1, 3, 5, 7, 9, 6} ∩ {1, 2, 3, 6, 9}
= {1, 3, 6, 9}
(d) (A ∪ B)
= (1, 3, 5, 7, 9, 6)
= {0, 2, 8, 4}
(e) A ∩ B
= {1, 3, 5, 7, 9} ∩ {3, 6, 9}
= {3, 9}
(f) (B ∪ A) ∩ C
= {3, 6, 9} ∪ {1, 3, 5, 7, 9} ∩ C
= {1, 3, 5, 7, 6, 9} ∩ {1, 2, 3, 6, 9}
= {1, 3, 6, 9}
Question no – (4)
Solution :
If A = {x : x ∈ W and 4 < x < 9}
= {5, 6, 7, 8}
B = {x : x ∈ N and 4 ≤ x ≤ 8}
= {4, 5, 6, 7, 8}
C = {natural numbers less than 5}
= {1, 2, 3, 4}
(a) A ∪ B
= {5, 6, 7, 8} ∪ {4, 5, 6, 7, 8}
= {4, 5, 6, 7, 8,}
(b) A ∩ B
= {5, 6, 7, 8} ∩ [4, 5, 6, 7, 8}
= {5, 6, 7, 8}
(c) A ∪ (B ∪ C)
= AV {4, 5, 6, 7, 8} ∪ {1, 2, 3, 4}
= A ∪ {1, 2, 3, 4, 5, 6, 7, 8,}
= {5, 6, 7, 8} ∪ {1, 2, 3, 4, 5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}
(d) A ∩ (B ∩ C)
= A ∩ [4, 5, 7, 8,} ∩ {1, 2, 3, 4}
= A ∩ {4}
= {5, 6, 7, 8} ∩ [4}
= ⌀
Operations on Sets Exercise 1.4 Solution
Question no – (1)
Solution :
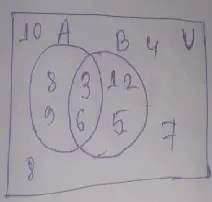
(a) U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {3, 6, 8, 9}
B = {1, 2, 3, 5, 6}
Venn diagram
(b) U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 5, 9}
B = {5, 8, 10}
C = {1, 2, 3, 4}
Here, the Venn diagram

(c) U = {BEAUTIFUL}
A = {B, U, F, T}
= C = {B, E, I, F}
Here, the diagram

Question no – (2)
Solution :

= From the Venn diagram, we find
= U = {a, b, c, d, e, f, g, h, i, j, k}
A = {a, c, d, e, f}
B = [e, f, b, g, h}
(a) A ∪ B
= {a, c, d, e, f} ∪ {e, f, b, g, h}
= {a, c, d, e, b, g, h}
(b) A ∩ B
= {a, c, d, e, f} ∩ {e, f, b, g, h}
= {e, f}
(c) A – B
= {a, c, d, e, f} – {e, f, b, g, h}
= [a, c, d}
(d) A1
= From the Venn diagram
= A = {b, g, h, i, j, k}
(e) B1
= From the Venn diagram,
B = {a, c, d, I, j, k}
(f) (A ∪ B)1
Now,
= A ∪ B = {a, c, d, e, f} ∪ {e, f, b, g, h}
= {a, b, c, d, e, f, g, h}
= (A ∪ B)1 = [I, J, K}
Question no – (3)
Solution :
Here, Let, U = {students]
A = {students who read newspaper A}
B = {students who read newspaper B}
C = {Students who read newspaper A and B}
Venn diagram,

(a) Number of students who read only newspaper A = 30 – 5
= 25
(b) Number of students who read only newspaper B = 20 – 5
= 15
(c) Number of students who read none of the newspapers = (30 + 20 + 5) – 50
= 55 – 50
= 5
Question no – (4)
Solution :
Here,
Let, U = {students}
A = {students who like black}
B = {students who like white}
Let, x be the number of students who like both black and white
So, the number of students who like only black 24 – x
Number of students who like only white = 18 – x

n (∪)= number of students who like only black + number of student who like only white + number of students who like both + number of students who like neither black nor white
= 24 – x + 18 – x + x + 5 = 40
= 47 – x = 40
= x = 7
∴ Seven students like both black and white.
Question no – (5)
Solution :
Let, the amount of pocket money of Meena {U} = x
∴ Spends amount of students of stationery = x/4 = {A}
∴ Spends amount of canteen = x/3 = {B}
A/Q,

x – (x/4 + x/3) = 40
= x – (3x + 4x/12) = 40
= x – 7x/12 = 40
= 12x – 7x/12 = 40
= 5x = 40 × 12
= x = 40 × 12/5
= 96
∴ Amount of pocket money = 96
Question no – (6)
Solution :
Given,
U = {x : x ∈ N, x ≤ 30}
= A {a : a ∈ U and a is even}
B = {b : b ∈ U and b is a multiple of 4}
Now,

A {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30}
B = [4, 8, 12, 16, 20, 24, 28}
(a) A ∪ B
= From the Venn diagram A ∪ B
= {2, 4, 6, 8, 10, 12, 16, 18, 20, 24, 26, 28, 30}
(b) A ∩ B
= From the Venn diagram
= {4, 8, 12, 16, 20, 24, 28}
(c) A – B
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30}
= – {4, 8, 12, 16, 20, 24, 28}
= {2, 6, 10, 14, 18, 22, 26, 30}
(d) B – A
= {4, 8, 12, 16, 20, 24, 28} – {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30}
= Փ
(f) n(A)
= n {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 24, 28, 30}
= 13
(g) n(B)
= n {4, 8, 12, 16, 20, 24, 28}
= 7
Now,
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ n(A ∪ B) = 7
n = (A ∪ B) = 14
R.H.S = n(A) + n(B) – n(A ∩ B)
= 14 + 7 – 7
= 14 = L.H.S (Proved)
Question no – (7)
Solution :
Let, U = {Students}
A = {Students passed in Hindi}
B = {Students passed in maths}
Let, x be the students passed in both the subject.
Venn diagram

∴ Number of students who passed only Hindi
= 90 – x
∴ Number of students who passed only maths = 80 – x
n (∪) = number of students who passed only Hindi + number of students who passed only maths + number of students who passed both + number of students who passed neither Hindi nor math.
= 90 – x + 80 – x + x + 6 = 100
= 176 – x = 100
= x = 76
Therefore, 76% students passed in both the subject.
Next Chapters Solutions :
Supper