Rd Sharma Solutions Class 8 Chapter 3 Squares and Square Roots
Welcome to NCTB Solution. Here with this post we are going to help 8th class students for the Solutions of RD Sharma Class 8 Mathematics, Chapter 3, Squares and Square Roots. Here students can easily find Exercise wise solution for chapter 3, Squares and Square Roots. Students will find proper solutions for Exercise 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8 and 3.9 Our teacher’s solved every problem with easily understandable methods so that every students can understand easily.
Squares and Square Roots Exercise 3.1 Solution :
Question no – (1)
Solution :
(i) 484
= Not Perfect Square.
(ii) 625
(25 × 25)
∴ It is perfect square.
(iii) 576
= (24 × 24)
∴ It is perfect square
(iv) 941
= Not perfect square
(v) 961
= (31 × 31)
∴ it is perfect square
(vi) 2500
= (50 × 50)
∴ It is perfect square.
Question no – (2)
Solution :
(i) 1156
= 2 × 1 × 17 × 17
= 2 × 17
= 34
(ii) 2025
= 3 × 3 × 3 × 3 × 5 × 5
= 3 × 3 × 5
= 45
(iii) 14611
= 11 × 11 × 11 × 11
= 11 × 11
= 212
(iv) 4761
= 3 × 3 × 23 × 23
= 3 × 23
= 69
Question no – (3)
Solution :
(i) 23805
= (3 × 3) (23 × 23) × 5
∴ 5 should be multiplied.
(ii) 12150
= 2 × (3 × 3) × (3 × 3) × (5 × 5)
∴ 2 should be multiplied.
(iii) 7688
= (31 × 31) × (2 × 2) × 2
∴ 2 should be multiplied.
Question no – (4)
Solution :
(i) 14283
= (23 × 23) × (3 × 3) × 3
∴ 3 should be divided
(ii) 1800
= (5 × 5) × (3 ×) × (2 × 2) × 2
∴ 2 should be divided
(iii) 2904
= (11 × 11) × (2 × 2) × 2 × 3
∴ 6 should be divided.
Question no – (5)
Solution :
From the above numbers the perfect square number are –
16 = 4 × 4
36 = 6 × 6
64 = 8 × 8
81 = 9 × 9
121 = 11 × 11
Question no – (6)
Solution :
The perfect square numbers are –
225 = 5 × 5 × 3 × 3
441 = 3 × 3 × 7 × 7
2916 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
11025 = 5 × 5 v 3 × 3 × 7 × 7
Question no – (7)
Solution :
(i) 8820
= (3 × 3) × (7 × 7) × (2 × 2) × 5
∴ 5 should be multiplied to get a perfect square.
∴ Required perfect square number = 44100 = 210 × 210
(ii) 3675
= (5 × 5) × 3 × (7 × 7)
∴ 3 should be multiplied
∴ Required perfect square number = 11025 = 105 × 105
(iii) 605
= (11 × 11) × (5 × 5) × 5
∴ 5 should be multiplied
∴ Required perfect square number = 3025 = 55 × 55
(iv) 2880
= 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5
∴ 5 should be multiplied
∴ Required perfect square number = 14400 = 120 × 120
(v) 4056
= (2 × 2) × (13 × 13) × 2 × 3
∴ 6 should be multiplied
∴ Required perfect square number = 24336 = 156 × 156
(vi) 3468
= (2 × 2) × (17 × 17) × 3
∴ 3 should be multiplied
∴ Required perfect square number = 10404 = 102 × 102
(vii) 7776
= (3 × 3) × (3 × 3) × 3 × (2 × 2) × (2 × 2) × (2 × 2) × 2
∴ 6 should be perfect multiplied
∴ Required perfect square number
= 46656
= 216 × 216
Question no – (8)
Solution :
(i) 16562
= (7 × 7) × (13 × 13) × 2
∴ 2 should be divided
∴ Required perfect square number
= 8281
= 91 × 91
(ii) 3698
= (43 × 43) × 2
∴ 2 should be divided
∴ Required perfect square number= 1849 = 43 × 43
(iii) 5103
= (3 × 3) × (3 × 3) × (3 × 3) × 7
∴ 7 should be divided
∴ Required perfect square number = 729 = 27 × 27
(iv) 3174
= (23 × 23) × 2 × 3
∴ 6 should be divided
∴ Required perfect square number = 529 = 23 × 23
(v) 1575
= (3 × 3) × (5 × 5) × 7
∴ 7 should be divided
∴ Required perfect square number = 225 = 15 × 15
Question no – (9)
Solution :
The greatest number of two digits which is a perfect square is – 81 = 9 × 9
Question no – (10)
Solution :
The least number of three digits which is perfect square is –
100 = 10 × 10
Question no – (11)
Solution :
Given number, 4851
= 3 × 3 × 7 × 7 × 11
∴ 11 should be multiplied.
∴ Required perfect square numbers,
= 3 × 3 × 7 × 7 × 11 × 11
= 53361
Question no – (13)
Solution :
Given number,
= 1152
= 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ 2 should be divided.
∴ Resulting square number
= 576
= 24 × 24
Squares and Square Roots Exercise 3.2 Solution :
Question no – (1)
Solution :
(i) 1547
= 7 × 13 × 17
∴ There are no pair
∴ it is not perfect square.
(ii) 45743
= 149 × 307
∴ There are no pair
∴ it is not perfect square.
(iii) 8943
= 271 × 2 × 2 × 2
∴ There are many number without pair.
∴ it is not perfect square.
(iv) 333333
= 3 × 3 × 11 × 7 × 37 × 13
∴ There are many number without pair.
∴ it is not perfect square.
Question no – (3)
Solution :
(i) 731
= odd number
(ii) 4058
= even number
(iii) 5559
= odd number
(iv) 42008
= even number.
Question no – (4)
Solution :
(i) 52
= unit digit
= 2²
= 4
(ii) 977
= unit digit
= 7² = 4 [9]
(iii) 4583
= unit digit
= 3²
= 9
(iv) 78367
= unit digit
= 7² 4 [9]
(v) 52698
= unit digit
= 8²
= 6 [4]
(vi) 99880
= unit digit
= 0
(vii) 12796
= unit digit
= unit digit
= 6²
= 3 [6]
(viii) 55555
= unit digit
= 5²
= 2 [5]
(ix) 53924
= unit digit
= unit digit
= 4²
= 1 [6]
Question no – (7)
Solution :
(i) 100² – 99²
= 100 + 99
= 199
(ii) 111² – 109²
= 111 + 109
= 219
(iii) 99² – 96²
= 99 + 96
= 195
Question no – (7)
Solution :
(i) (8, 15, 17)
= (15)² + (8)² = (17)²
= 289 = 289
∴ It is Pythagorean Triplets
(ii) (18, 80, 82)
= (18)² + (80)² = (82)²
= 6724 = 8724
∴ It is Pythagorean Triplets
(iii) (14, 48, 5)
= (14)² + (48)² = (51)²
= 2000 ≠ 2601
∴ It is not Pythagorean Triplets
(iv) (10, 24, 26)
= (10)² + (24)² = (26)²
= 676 = 676
∴ It is Pythagorean Triplets
(v) (16, 63, 65)
= (16)² + (63)² = (65)²
= 4225 = 4225
∴ It is Pythagorean Triplets
(vi) (12, 35, 38)
= (2)² + (35)² = (38)²
= 1369 ≠ 1444
∴ It is not Pythagorean Triplets.
Question no – (8)
Solution :
Given numbers,
= (1 × 2) + (2 × 3) + (3 × 4) + (4 × 5) + (5 × 6)
= 5 × 6 × 7/ 3
= 210/3
= 70
Therefore, the value will be 70.
Question no – (9)
Solution :
(i) 1 + 2 + 3 + 4 + 5 + … + 50
= 1/2 {50 × (50 + 1)}
= 1/2 × 50 × 51
= 1275
(ii) 31 + 32 + … + 50
= An = 50
a = 31
Common difference = d = 32 – 31 = 1
∴ An = a + (n – 1) × d
or, 50 = 31 + (n – 1) × 1
or, (n – 1) = 50 – 31 = 19
or, n = 19 + 1 = 20
∴ Sn = n/2 (2a + (n-1) d)
= 20/2 (2 × 31 + (20 – 1) 1)
= 10 [62 + 10]
= 10 × 81 = 810
Question no – (11)
Solution :
The squares of even numbers are, 256, 324, 1296, 5476
Question no – (12)
Solution :
(i) 1026
= unit digit
= 6 cannot be square.
(ii) 1028
= unit digit
= 8 = It may be a square.
(iii) 1024
= unit digit
= 2 = It may be a square.
(iv) 1022
= unit digit
= 3
∴ It cannot be perfect square.
(v) 1023
= unit digit
= 3
∴ It cannot be perfect square.
(vi) 1027
= unit digit
= 7
∴ It cannot be a perfect.
Question no – (13)
Solution :
The five numbers are,
(i) 12461
(ii) 5680
(iii) 1734
(iv) 915389
(v) 25247
Question no – (14)
Solution :
When unit digit of a number end with ‘0’ ‘7’ ‘3’ ‘2’ then it will be not square. Example – 520, 47, 1753, 4122, 1980
Question no – (15)
Solution :
(i) The number of digits in a perfect square is even – (False).
(ii) The square of a prime number is prime – (False).
(iii) The sum of two square numbers is a square number – (False).
(vi) No square number is negative – (True).
(vii) There is no square number between 50 and 60 – (True).
(viii) There are fourteen square number up to 200 – (True).
Squares and Square Roots Exercise 3.3 Solution :
Question no – (1)
Solution :
(i) 25 = a = 2, b = 5
| Col – I | Col – II | Col – III |
| a ² | 2 × a × b | b² |
| 2 ² | 2 × 2 × 5 | 5² |
| 4 | 20 | 25 |
| +2 | + 2 | 5 |
| 6 | 22 | |
| 2 |
∴ (25)² = 625
(ii) 37 = a = 3 b = 7
| Col – I | Col – II | Col – III |
| a ² | 2 × a × b | b² |
| 3² | 2 × 3 × 7 | 7² |
| 9 | 42 | 49 |
| + 4 | + 4 | 9 |
| 13 | 46 | |
| 6 |
∴ (37)² = 1369
(iii) 54 = a = 5 = b = 4
| Col – I | Col – II | Col – III |
| a² | 2 × a × b | b² |
| 5² | 2 × 5 × 4 | 4² |
| 25 | 40 | 16 |
| + 4 | + 1 | 6 |
| 29 | 41 | |
| 1 |
∴ (54)² = 2916
(iv) 71 = a = 7, b = 1
| Col – I | Col – II | Col – III |
| a² | 2 × a × b | b² |
| 7² | 2 × 7 × 1 | 1² |
| 49 | 14 | 1 |
| + 1 | + 0 | 1 |
| 50 | 14 | |
| 4 |
∴ (71)² = 5041
(v) 96 = a = 9 b = 6
| Col – I | Col – II | Col – III |
| a² | 2 × a × b | b² |
| 9² | 2 × 9 × 6 | 6² |
| 81 | 108 | 36 |
| + 11 | + 3 | 6 |
| 92 | 111 | |
| 1 |
∴ (96)² = 9216
Question no – (2)
Solution :
(i) 98
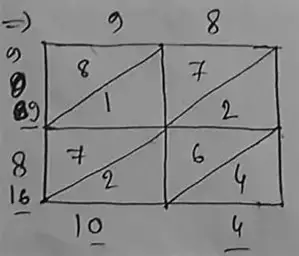
∴ (98)² = 9606
(ii) 273
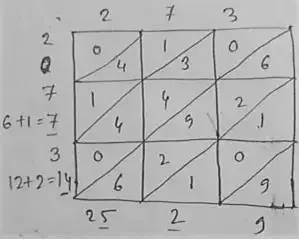
∴ (273)² = 7452
(iii) 348
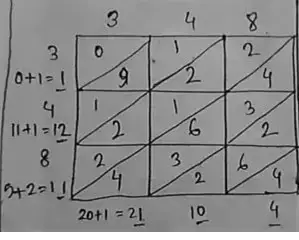
∴ (348)² = 121104
(iv) 295
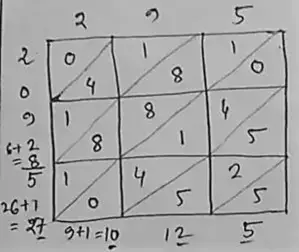
∴ (295)² = 87025
(v) 171
∴ (171)² = 29241
Question no – (4)
Solution :
(i) 425
= (425)²
= 425 ×425
= 180625
(ii) 575
= (575)²
= 575 × 575
= 330625
(iii) 405
= (405)²
= 405 × 405
= 164025
(iv) 205
= (205)²
= 205 × 205
= 42025
(v) 95
= (95)²
= 95 × 95
= 9025
(vi) 745
= (745)²
= 745 × 745
= 555025
(vii) 512
= (512)²
= 512 × 512
= 262144
(viii) 995
= (995)²
= 995 × 995
= 990025
Question no – (5)
Solution :
(i) 405
405 = (400 + 5)²
= (400) ² + 2.400. 5 + 5²
= 160000 + 4000 + 25
= 164025
(ii) 510
510 = (500 + 10)²
= (500) ² + 2. 500 .10 + (10) ²
= 250000 + 10000 + 100
= 260100
(iii) 1001
= 1001 = (100 + 1)²
= (1000) ² + 2. 1000. 1 + 1²
= 1000000 + 2000 + 1
= 1002001
(iv) 209
209 = (200 + 9)²
= (200) ² + 2. 200.9 + 9²
= 40000 + 3600 + 81
= 43681
(v) 605
605 = (600 + 5)² (600)² 2. 600. 5 + 5²
= 360000 + 6000 + 25
= 366025
Question no – (7)
Solution :
(i) 52
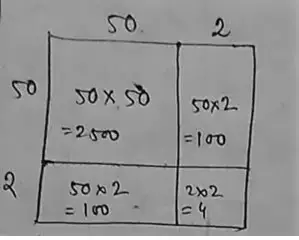
∴ (52)² = 2500 + 100 + 100 + 4
= 2704
(ii) 95
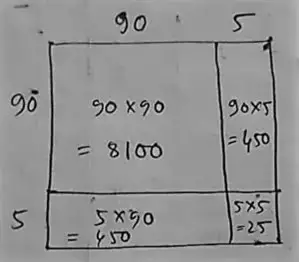
∴ (95)² = 8100 + 450 + 450 = 25
= 9025
(iii) 505
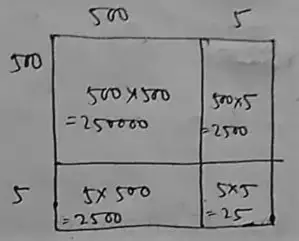
∴ (505)² = 250000 + 2500 + 2500 + 25
= 255025
(iv) 702
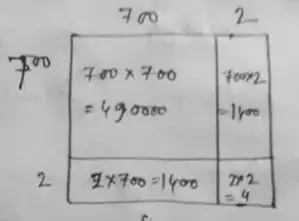
∴ (702)2 = 490000 + 1400 + 1400 + 4
= 492804
(v) 99
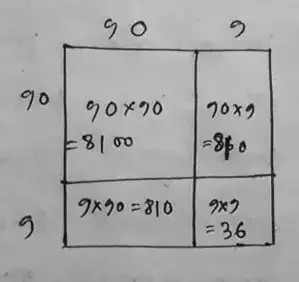
∴ (99)² = 8100 + 810 + 810 + 36
= 9801
Squares and Square Roots Exercise 3.4 Solution :
Question no – (1)
Solution :
(i) 9801
= unit digit 1 → 1 or 9
∴ odd square root
(ii) 99856
= unit digit 1 →1 or 6
∴ odd square root
(iii) 998001
= unit digit 1 → 1 or 9
∴ odd square root
(iv) 6576625
= unit digit 5 → 5
∴ odd square root.
Question no – (2)
Solution :
(i) 441
= √441 = √ 3 × 3 × 7 × 7
= 3 × 7
= 21
(ii) 196
= √196 = √2 × 2 × 7 × 7
= 2 × 7
= 14
(iii) 529
√529 = √23 × 23
= 23
(iv) 1764
= √1764 = √2 × 2 × 3 × 3 × 7 × 7
= 2 × 3 × 7
= 42
(v) 1156
= √1156 = √2 × 2 × 17 × 17
= 2 × 17
= 34
(vi) 4096
= √4096 = √2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2 × 2 × 2 × 2 × 2 × 2
= 64
(vii) 7056
= √7056 = √2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
= 2 × 2 × 3 × 7
= 84
(viii) 8281
= √8281 = √7 × 7 × 13 × 13
= 7 × 13
= 91
(ix) 11664
= √11614 = √2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
= 2 × 2 × 3 × 3 × 3
= 108
(x) 47089
= √47089 = √7 × 7 × 31 × 31
= 7 × 13
= 217
(xi) 24336
= √24336 = √2 × 2 × 2 × 2 × 3 × 3 × 13 × 13
= 2 × 2 × 3 × 13
= 156
(xii) 190969
= √190969 = √19 × 19 × 23 × 13
= 19 × 23
= 437
(xiii) 586756
= √586756 = √2 × 2 × 383 × 383
= 2 × 383
= 766
(xiv) 27225
∴ √27225 = √3 × 3 × 5 × 5 × 11 × 11
= 3 × 5 × 11
= 165
(xv) 3013696
= √3013696 = √2 × 2 × 2 × 2 × 2 × 2 × 217 × 217
= 2 × 2 × 2 × 217
= 1736
Question no – (3)
Solution :
Dear students, we can solve the problem as follows :
180 = (2 × 2) × 93 × 3) × 5
∴ 5 is unpaired so 5 should be multiplied.
∴ New required number = 2 × 2 × 3 × 5 × 5 = 900
√900 = √30 × 30 = 30
Question no – (4)
Solution :
147 = 3 × 7 × 7
∴ 3 is unpaired so 3 should be multiplied.
∴ New required number,
= 3 × 3 × 7 × 7
= 441
∴ √441 = √21 × 21 = 21
Question no – (5)
Solution :
3645 = 3 × 3 × 3 × 3 × 3 × 3 × 5
∴ 5 is unpaired so 5 should be divided.
∴ New required number
= 3 × 3 × 3 × 3 × 3 × 3
= 729
∴ √729 = √27 × 27
= 27
Question no – (6)
Solution :
1152 = (2 × 2) × (2 × 2) × (2 × 2) × 2 × (3 × 3)
∴ 2 is unpaired so ‘2’ should be divided.
∴ New required number,
= 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
= 576
∴ √576 = √24 × 24
= 24
Question no – (7)
Solution :
Let, One number = x
∴ Other, 16x
According to question –
x × 16x = 1296
or, 16x² = 1296
or, x² = 1296/16 = 81
or, x = √81 = 9
∴ One number = 9
∴ Another number = 9 × 16 = 144
Question no – (8)
Solution :
Total collected many = 202500
∴ Each paid as money rupees there were resident,
∴ The number of resident = √202500
= √5 × 5 × 5 × 5 × 2 × 2 × 3 × 3 × 3
= 5 × 5 × 2 × 3 × 3
= 450
Therefore, the number of residents are 450.
Question no – (9)
Solution :
Total collected = 92.16 = 9216/100
∴ member collected as many paise as there were members.
∴ there no of member = √9216/100 = contribution of members
∴ √9216/100
= √96 × 96/10 × 10
= 96/10
= 9.6 Paise.
Question no – (10)
Solution :
Total collected fees = 2304
The number of students,
= √2304
= √2 × 2 × 2 × 2 × 2 × 2 × 2 × 2× 3 × 3
= 2 × 2 × 2 × 2 × 3
= 48
Therefore, there are 48 students in the school.
Question no – (11)
Solution :
Given in the question,
Area of square = 5184 m²
∴ One side of square,
= √5184 = √72 × 72
= 72
∴ Perimeter of square,
= 4 × 72
= 288 m
Let, breadth of rectangle = x
Length of rectangle = 2x
According to question –
2 (x + 2x) = 288
or, 3x = 288/2 = 144
or, x = 144/3 = 48 m
∴ Breadth = 48 m
Length = 2 × 48 = 96 m
∴ Area of rectangular,
= 48 × 96
= 4608 m²
Thus, the area of the rectangular field is 4608 m².
Question no – (12)
Solution :
(i) L.C.M 6, 9, 15, 20 is = 180
180 = (2×2×3×3) × 5
To make perfect square, multiply it by 5.
∴ Required number = (180 × 85) = 900
Thus, the least square number is 900.
(ii) Taking L.C.M, of 8, 12, 15, 20
L.C.M = 4×3×5×2 = 120
= (2×2×3×5×2)
To make it perfect square multiply it by 30
∴ Required number,
= (120 × 30)
= 3600
Thus, the least square number is 3600.
Question no – (13)
Solution :
(i) 121
= 121 – 1 = 120
120 – 3 = 117
117 – 5 = 112
112 – 7 = 105
105 – 9 = 96
96 – 11 = 85
85 – 13 = 72
72 – 15 = 57
57 – 17 =40
40 – 19 = 21
21 – 21 = 0
∴ There are 11 number subtracted.
∴ √121 = 11
(ii) 169
= 169 – 1 = 168
168 – 3 = 165
165 – 5 = 160
160 – 7 = 153
153 – 9 = 144
144 – 11 = 133
133 – 13 = 120
120 – 15 = 120
120 – 15 = 105
105 – 17 = 88
88 – 21 = 48
48 – 23 = 25
25 – 25 = 0
∴ There are 13 numbers subtracted.
∴ √169 = 13
Question no – (14)
Solution :
(i) 7744
= √7744 = √2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
= 2 × 2 × 2 × 11
= 88
(ii) 9604
= √9604 = √2 × 2 × 7 × 7 × 7 × 7
= 2 × 7 × 7
= 98
(iii) 5929
= √5929 = √7 × 7 × 11 × 11
= 7 × 11
= 77
(iv) 7056
= √7056 = √2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
= 2 × 2 × 3 × 7
= 84
Question no – (15)
Solution :
Total student contributed = 2401
∴ The number of student,
= √2401
= √7 × 7 × 7 × 7
= 7 × 7
= 49
Therefore, the number of students in the class is 49.
Question no – (16)
Solution :
Total student = 6000
Student left,
= 6000 – 71
= 5929
∴ The number of row
= √5929
= √7 × 7 × 11 × 11
= 7 × 11
= 77
∴ The number of rows are 77
Squares and Square Roots Exercise 3.5 Solution :
Question no – (1)
Solution :
(i) 12544
long division method :
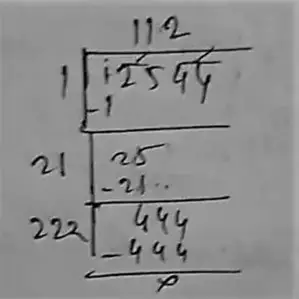
∴ Square root of 12544 is 112.
(ii) 97344
long division method :
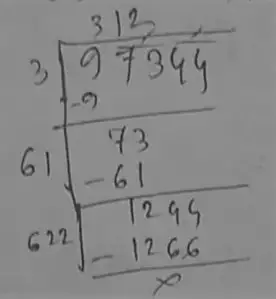
So, the square root of 97344 is = 312
(iii) 286225
long division method :
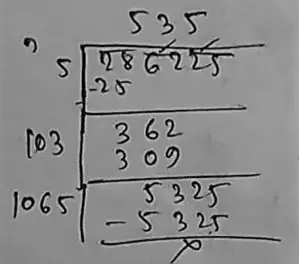
∴ The square root of 286225 is = 535
(v) 363609
long division method :
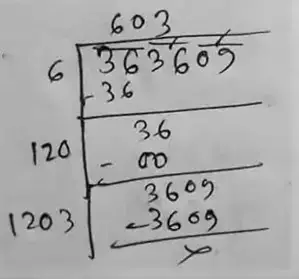
So, the square root of 363609 is = 603
(vi) 974169
long division method :
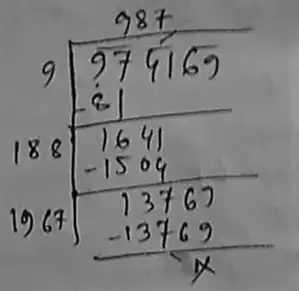
So, the square root of 974169 is = 987
(vii) 120409
long division method :
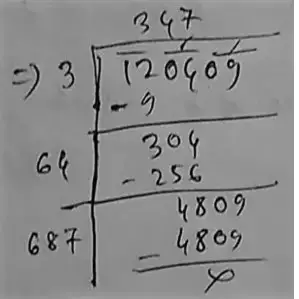
∴ The square root of 120409 is = 347
(viii) 1471369
long division method :
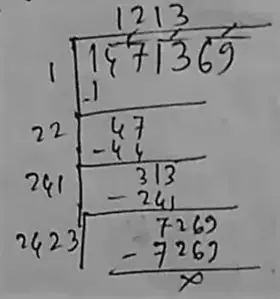
Thus, the square root of 1471369 is = 1213
(ix) 291600
Long division method :
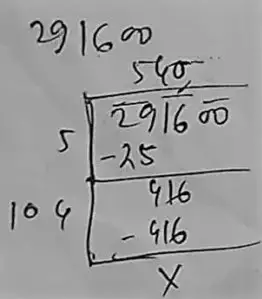
So, the square root of 291600 is = 540
(x) 9653449
Long division method :
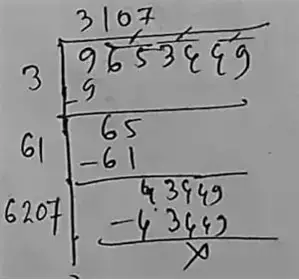
So, the square root of 9653449 is = 3107
(xi) 1745041
Long division method :

Thus, the square root of 1745041 is = 1321
(xii) 4008004
long division method :
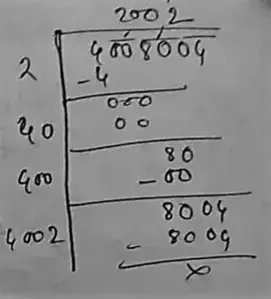
∴ The square root of 4008004 is = 2002
(xiii) 20657025
Long division method :
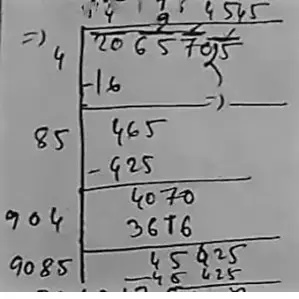
So, the square root of 20657025 is = 4545
(xiv) 152547201
Long division method :

Thus, the square root of 152547201 is = 12351
(xv) 20421361
Long division method :
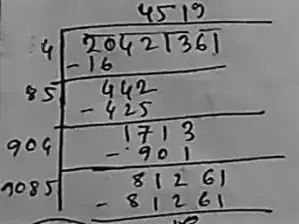
So, Square root of 20421361 is = 4519.
(xvi) 62504836
Long division method :

∴ The square root of 62504836 is = 7906.
(xvii) 82264900
Long division method :

Thus, the square root of 82264900 is = 9070
(xviii) 3226694416
Long division method :
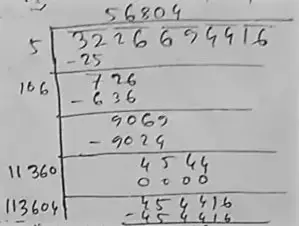
So, the square root of 3226694416 is = 56804
(xix) 6407522209
Long division method :
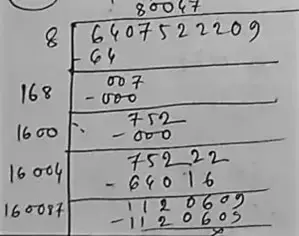
∴ The square root of 6407522209 is = 80047
(xx) 3915380329
Long division method :

So, the square root of 3915380329 is = 62573
Question no – (2)
Solution :
(i) 2361
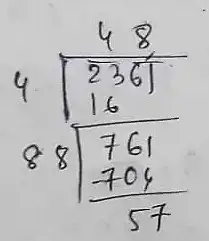
∴ 57 should be subtracted
(ii) 194491

∴ 10 should be subtracted
(iii) 26535
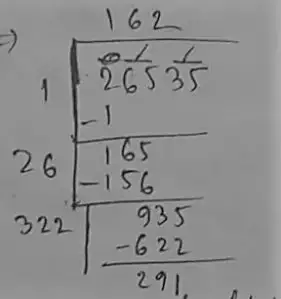
∴ 291 should be subtracted
(iv) 16160

∴ 31 should be subtracted
(v) 4401624
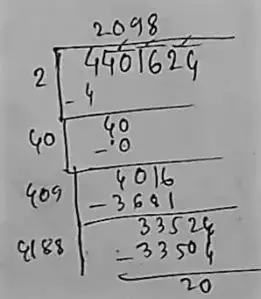
∴ 20 should be subtracted.
Question no – (3)
Solution :
(i) 5607
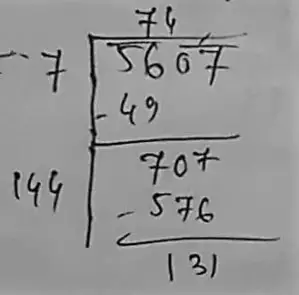
∴ 131 should be added.
(ii) 4931
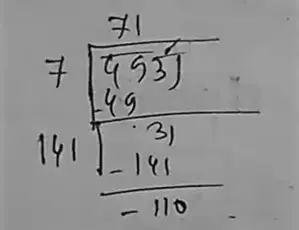
∴ 110 should be added.
(iii) 4515600
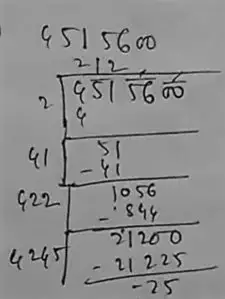
∴ 25 should be added.
(iv) 37460
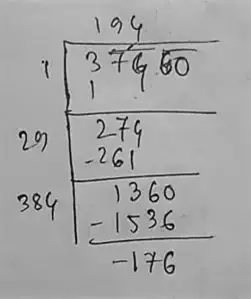
∴ 176 should be added.
(v) 506900
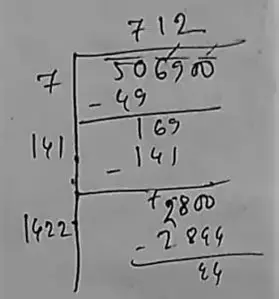
∴ 44 should be added.
Question no – (4)
Solution :
The greatest number of 5 digit which a perfect square is 99856.
Question no – (5)
Solution :
The least number of 4 digits which a perfect square is 1024
Question no – (6)
Solution :
The least number of Six digits perfect square is 100489
Question no – (7)
Solution :
The greatest number of 4 digit perfect square 9801
Question no – (8)
Solution :
Total number = 8160
∴ Left = 60
∴ The number of soldier,
= 8160 – 60 = √8100
= √90 × 90
= 90
Therefore, the number of soldiers in each row is 90.
Question no – (9)
Solution :
Let, The One side of square = x
∴ Area one side of square = x²
According to question,
x² = 60025
or, x = √60025
= √245 × 245
= 245 m
∴ Perimeter of square,
= 245 × 4
= 980 m
= 0.98 km
A man cycles in 1 hr. 18 km
∴ A man cycles in 1 hr,
= 0.98/18
= 0.054 hr.
= 3 min 16 sec
Thus, in 3 min 16 sec he return at the starting point.
Question no – (10)
Solution :
Total cost of leveling and turfing a square = 13322.50
Total cost of leveling and turfing a square = 2.50/ per m²
∴ Total cost of leveling and turfing a square in 1 square m²
= 13222.50/2.50
= 5329 m²
Let, outside of square = x
∴ According to question –
x² = 5329
or, x = √5329 = 73 m
∴ Perimeter of square,
= 4 × 73
= 292 m
∴ Cost of perfect at 5 per metre,
= 292 × 5
= 1460
∴ The cost of fencing it at Rs 5 per metre is Rs. 1460.
Question no – (11)
Solution :
The greatest number of 3 digit of perfect square is 961
Question no – (12)
Solution :
Given number, 2300
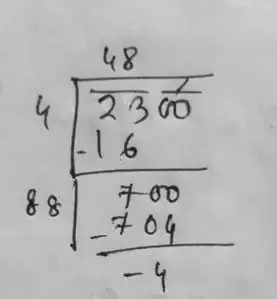
∴ 2300 < (48)2
∴ 4 should be added.
Squares and Square Roots Exercise 3.6 Solution :
Question no – (1)
Solution :
(i) 441/961
= √441/√961
= √21 × 21/√31 × 31
= 21/31
(ii) 324/841
= √324/√841
= √18 × 18/√29 × 29
= 18/29
(iv) 2 14/25
= √64/√25
= √8 × 8/√5 × 5
= 8/5
(v) 2 137/196
= √529/√196
= √23 × 23/√14 × 14
= 23/14
(vi) 23 26/121
= √2809/√121
= √53 × 53/√11× 11
= 53/11
(vii) 25 444/729
= √17311/√729
= √137 × 137/√27 × 27
= 137/27
(viii) 75 46/49
= √3721/√49
= √61 × 61/√7 × 7
= 61/7
(ix) 3 942/2209
= √7569/√2209
= √87 × 87/√47 × 47
= 87/47
(x) 3 334/3025
= √9409/√3025
= √97 × 97/√55 × 55
= 97/55
(xi) 21 2797/3364
= √73441/√3364
= √271 × 271/√58 × 58
= 271/58
(xii) 38 11/25
= √961/√25
= √31 × 31/√5 × 5
= 31/5
(xiii) 23 394/729
= √17161/729
= √131 × 131/√27 × 27
= 131/27
(xiv) 21 51/169
∴ √3600/169
= √60 × 60/√13 × 13
= 60/13
(xv) 10 151/225
∴ √2401/225
= √49 × 49/√15 × 15
= 49/15
Question no – (2)
Solution :
(i) √80/√405
= √2 × 2 × 2 × 2 × 5/ √3 × 3 × 3 × 3 × 5
= 2 × 2 √5 / 3 × 3 √5
= 4/9
Therefore, the value will be 4/9.
(ii) √441/ √625
= √21 × 21/25 × 25
= 21/25
Therefore, the value will be 21/25
(iii) √1587/1728
= √3 × 23 × 23 /√2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
= 23 √3 /2 × 2 × 2 × 3√3
= 23/24
Hence, the value will be 23/24
(iv) √72 × √338
= √2×2×2×3×3 × √2×13×13
= 3 × 2 × 2 × 13
= 156
Thus, the value will be 156.
(v) √45 × √20
= √5×3×3 × √2×2×5
= 5 × 2 × 3
= 30
Thus, the value will be 30.
Question no – (3)
Solution :
Area of square,
= 80 224/179
= 58564/729 m²
∴ Side of the square,
= √58564/729
= √242 × 242/√27× 27
= 242/27
= 8 26/27 m
Therefore, the length of each side of the field will be 8 26/27 m.
Question no – (4)
Solution :
Area of square,
= 30 1/4
= 121/4 m²
∴ One side square,
= √121/4
= 11/2
= 5 1/2 m
Therefore, the length of the sides of the square will be 5 1/2 m.
Question no – (5)
Solution :
Area to rectangular field,
= 72 × 338
= 24336 m²
According to question
∴ Area of rectangular,
= 24336 m² = Area of square field.
∴ One side of square field,
= √24336
= √156 √ 126
= 156 m.
Thus, the length of side of square playground is 156 m.
Squares and Square Roots Exercise 3.7 Solution :
Question no – (1)
Solution :
Given number, 84.8241
= 848241/10000
= √921 × 921/ 100 × 100
= 921/100
= 9.21…(In decimal form)
Question no – (2)
Solution :
Given number, 0.7225
= 7225/10000
= √85 × 85 /100 × 100
= 85/100
= 0.85…(In decimal form)
Question no – (3)
Solution :
Given number, 0.813604
= 813604/1000000
= √902 × 902/1000 × 1000
= 902/10000
= 0.902…(In decimal form)
Question no – (4)
Solution :
Given number, 0.00002025
= 2025/100000000
= √45 × 45/10000 × 10000
= 45/10000
= 0.0045…(In decimal form)
Question no – (5)
Solution :
From the question, 150.0625
= 1500625/10000
= √1225 × 1225/100 × 100
= 1225/100
= 12.25…(In decimal form)
Question no – (6)
Solution :
Given number, 225.6004
= 2256004/10000
= √1502 × 1502/100 × 100
= 1502/100
= 15.02…(In decimal form)
∴ The square root of 225.6004 is 15.02
Question no – (7)
Solution :
Given number, 3600.720036
∴ 3600720036/100000
= √60006 × 60006/ 1000 × 1000
= 60006/1000
= 60.006…(In decimal form)
Hence, square root of 3600.720036 is 60.006
Question no – (8)
Solution :
From the question, 236.144689
= 236144689/1000000
= √15367 × 15367/ 1000 × 1000
= 15367/10000
= 15.367…(In decimal form)
Thus, the square root of 236.144689 is 15.367
Question no – (9)
Solution :
Given number, 0.00059049
= 59049/100000000
= √243 × 243/ 10000 × 10000
= 243/10000
= 0.0243…(In decimal form)
Thus, the square root of 0.00059049 is = 0.0243
Question no – (10)
Solution :
From the question, 176.252176
= 176252176/1000000
= √13276 × 13276/ 1000 × 1000
= 13276/1000
= 13.276…(In decimal form)
Hence, the square root of 176.252176 is 13.276
Question no – (11)
Solution :
Given number, 9998.0001
= 99980001/10000
= √9999 × 9999/ 100 × 100
= 9999/100
= 99.99…(In decimal form)
∴ The square root of 9998.0001 is 99.99
Question no – (12)
Solution :
Given, 0.00038809
= 38809/100000000
= 197 × 197/ 10000 × 10000
= 197/10000
= 0.0197…(In decimal form)
Therefore, the square root of 0.00038809 is 0.0197
Question no – (13)
Solution :
From the question we get,
227.798649
= √227798649/1000000
= √15093 × 15093/ 1000 × 1000
= 15093/1000
= 15.093
Therefore, the required fraction will be 15.093
Question no – (14)
Solution :
A per the given question,
Area of square playground = 256.6406 m²
∴ One side square playground,
= √256.6404
= √2566404/10000
= √1602 × 1602/ 100×100
= 16.02 m
Hence, the length of one side of the playground will be 16.02 m.
Question no – (15)
Solution :
Given, 0.00053361
∴ √53361/ 100000000
= √231 × 231/ 10000 × 10000
= 231/10000
= 0.0231
Thus, the required fraction will be 0.0231
Question no – (16)
Solution :
(i) √59.29 – √5.29/√59.29 + √5.29
= (√59.29 – 5.29) (59.29 – √5.29)/(59.29 + √5.29) (√59.29 – √5.29)
= (√59.29 – √5.29)/(59.29) – (√5.29)²
= (59.29) – 2 × √59.29 √5.29 + (√5.29)²/ 59.29 – 5.29
= 59.29 + 5.29 – 2 × (√5929/ 100 × 529/100)/54
= 64.58- (2 × √77 × 77/ 10 × 10 × 23 × 23/10 × 10/54)
= 64.58 – (2 × 7 × 23/10 × 10)/54
= 64.58 – 3542/100/54 = 64.58 – 35.42/54
= 29.16/54
= 0.54…(Simplified)
(ii) √0.2304 + √0.1764/√0.2304 – √0.1764
= 0.2304 + √0.1764/ 0.2304 – √0.1764
= (√0.2304 + √0.1764) (√0.2304 + √0.1764)/(√0.2304 – √0.1764) (√0.2304 + √0.1764)
= (√0.2304 + (√0.1764)²/ (√0.2304)² – (√0.1764)²
= (√0.2304)² + 2 × √0.2304 × √0.1764 + (√0.1764)²/ 0.2304 – 0.1764
= (0.2304 + 0.1764) – 2 × √2304/10000 × 1764/1000/ 0.54
= (0.4068 – 2√48×48/ 100 × 100)/0.054
= 0.4068 – (2 × 48/100 ×48/100)
= 0.4068- (4032/10000)/0.054
= 0.4068 – 0.4032/0.054
= 0.0036/0.054
= 0.0060…(Simplified)
Question no – (17)
Solution :
Evaluate √50625
= √225 × 225
= 225
Now, the value of √506.25 + √5.0625
= √50625/100 + √50625/10000
= 225/10 + 225/100
= 225 + 225/100
= 2475/100
= 24.75
Therefore, the value is 24.75
Question no – (18)
Solution :
The value of, √130.0225
= √103.0225/√10000
= √1015 × 1015/√100 × 100
= 1015/100
= 10.15
The value of, (i) √10302.25
= √10302.25/100
= √1015 × 1015/10 × 10
= 1015/10
= 101.5
Thus, the value will be 101.5
The value of, (ii) √1.030225
= √1.030225/1000000
= √1015 × 1015/1000 × 1000
= 1015/1000
= 1.015
Therefore, the value will be 1.015
Squares and Square Roots Exercise 3.8 Solution :
Question no – (1)
Solution :
(i) Given number, 5
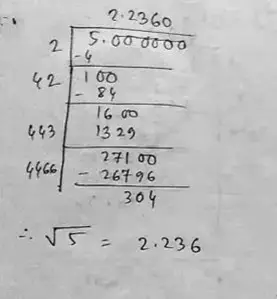
∴ √5 = 2.236
So, square root of 5 correct to three places of decimal is 2.236.
(ii) Given number, 7
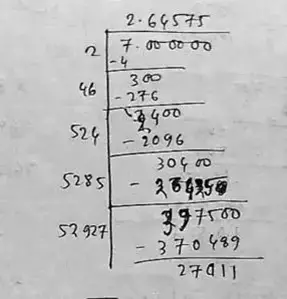
∴ √7 = 2.646
So, the square root of 7 correct to three places of decimal is 2.646
(iii) Given number, 17
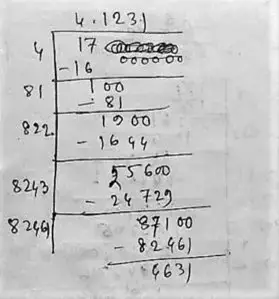
∴ √17 = 4.123
So, the square root of 17 correct to three places of decimal is 4.123
(iv) Given number, 20

∴ √20 = 4.472
Hence, the square root of 20 correct to three places of decimal is 4.472
(v) Given number, 66
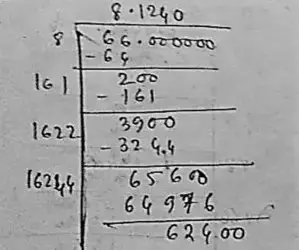
∴ √66 = 8.1240
Thus, the square root of 66 correct to three places of decimal is 8.1240
(vi) We have, 427

∴ √427 = 20.664
Hence, the square root of 427 correct to three places of decimal is 20.664
(vii) We have, 1.7
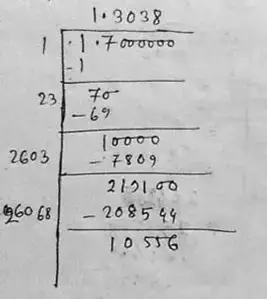
∴ √1.7 = 1.304
Therefore, the square root of 1.7 correct to three places of decimal is 1.304
(viii) Given number, 23.1
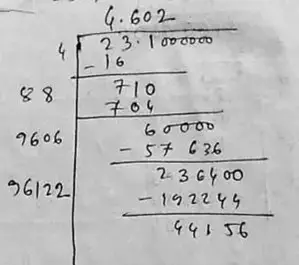
∴ √23.1= 4.602
Thus, the square root of 23.1 correct to three places of decimal is 4.602
(ix) Given number, 2.5
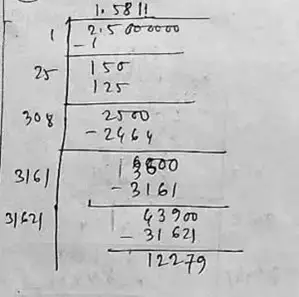
∴ √2.5 = 1.5811
∴ The square root of 2.5 correct to three places of decimal is 1.5811
(x) Here we have, 237.615
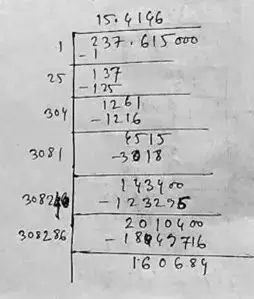
∴ √237.615 = 15.415
So, the square root of 237.615 correct to three places of decimal is 15.415
(xi) We have, 15.3215
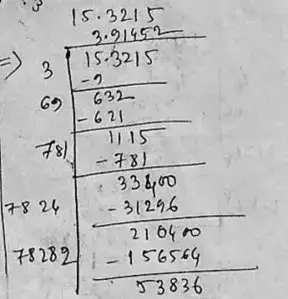
∴ √15.3215 = 3.914
So, the square root of 15.3215 correct to three places of decimal is 3.914
(xii) Given number, 0.9
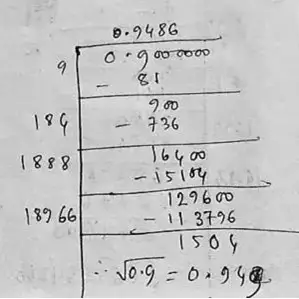
∴ √0.9 = 0.949
So, the square root of 0.9 correct to three places of decimal is 0.949
(xiii) Here we have, 0.1

∴ √0.1 = 0.316
Hence, the square root of 0.1 correct to three places of decimal is 0.316
(xiv) Given number, 0.016

∴ √0.16 = 0.126
∴ The square root of 0.16 correct to three places of decimal is 0.126
(xv) Given number, 0.00064
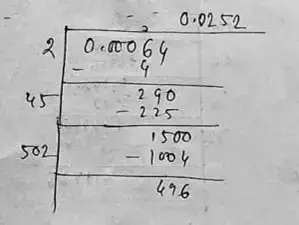
∴ √0.00064 = 0.025
Hence, the square root of 0.00064 correct to three places of decimal is 0.025
(xvi) Here we have, 0.019
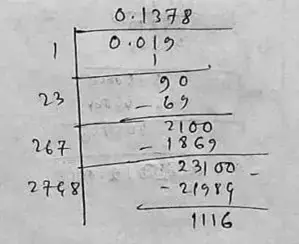
∴ √0.019 = 1.138
So, the square root of 0.019 correct to three places of decimal is 1.138
(xvii) Given number, 5/12
= 0.41666666
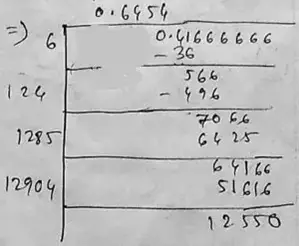
∴ √5/12 = 0.645
Hence, the square root of 5/12 correct to three places of decimal is 0.645
(xviii) Given in the question, 12.0068

∴ √12.0068 = 3.4651
So, the square root of 12.0068 correct to four decimal places 3.4651.
Question no – (2)
Solution :
Given in the question, 12.0068

∴ √12.0068 = 3.4651
Therefore, the square root of 12.0068 correct to four decimal places 3.4651.
Question no – (3)
Solution :
Given in the question, 11

∴ √11 = 3.31662
Hence, the square root of 11 correct to five decimal places is 3.31662
Question no – (4)
Solution :
(i) √144/7
= √11 × 11 /√7
= 11/√7
= √11 √ 7/ √7 × √7
= 11√7/7
= 11 × 2.646/7
= 4.536
(ii) √23500/3
= √2500/√3
= √50 × 50/√3
= 50/√3 = 50√/√3 × √3
= 50√3/3
= 50 × 1.732/3
= 28.867
Question no – (5)
Solution :
(i) 196/75
√196/√75 = √2 × 2 × 7 × 7/ 3 × 5 × 5
= 2 × 7/ 5 √3
= 14/ 5 × 1.732
= 1.617
(ii) 400/63
×400/63 = √2 × 2 × 2 × 2 × 5 × 5/ √2 × 3 × 3 × 3
= 2 × 2 × 5/ 3 × √2 × √3
= 20/ 3 × 1.412 × 1.732
= 2.520
(iii) 150/7
√150/√7 = √3 × 2 × 5 × 5/ √7
= √3 × √2 × 5 /√7
= 1.412 × 1.732 × 5/2.646
= 4.628
(iv) 256/5
√256/√5 = √2 × 2 × 2 × 2× 2 × 2 × 2 × 2/√5
= 2 × 2 × 2 × 2/2.236
= 8/2.236
= 7.155
(v) 27/50
√27/50 = √3 × 3 × 3 / √2 × 5 × 5
= 3 √3/5 √2
= 3 × 1.732/ 5 × 1.414
= 0.735
Squares and Square Roots Exercise 3.9 Solution :
Question no – (1)
Solution :
Given, 7
√7 = 2.646
Question no – (2)
Solution :
Given, 15
√15 = 3.873
Question no – (3)
Solution :
Given, 74
√74 = 8.602
Question no – (4)
Solution :
Given, 82
√82 = 9.055
Question no – (5)
Solution :
Given, 198
√198 = √2 × 3 × 11
= 1.414 × 1.732 × 3.317
= 14.070
Question no – (6)
Solution :
Given, 540
√540 = √2 × 5 × 3 × 3 × 3 × 2
= 2 × 3 √15 = 6 × 3.873
= 23.24
Question no – (7)
Solution :
Given, 8700
√8700 = √87 × 100 × 10
= 10 √87 = 10 × 9.327
= 9327
Question no – (8)
Solution :
Given, √3509
√3500 = √11 × 11 × 29
= 11 √29 = 11 × 5.385
= 59.235
Question no – (9)
Solution :
Given, 6929
√6929 = √13 × 13 × 41 = 13 √41
= 13 × 6.40
= 83.239
Question no – (10)
Solution :
Given, 25725
√25725 = √3 × 5 × 5 × 7 × 7 × 7
= 5 × 7 √3 × 7
= 35 √21
= 35 × 4.583
= 157.78
Question no – (11)
Solution :
Given, 1312
√13123 = √2 × 2 × 2 × 2 × 2 × 41 = 2 × 2 √82
= 4 × 9.055 = 36.22
Question no – (12)
Solution :
Given, 4192
√4192 = √2 × 2 × 2 × 2 × 131
Question no – (13)
Solution :
Given, 4955
√5955 = √5 × 99
Question no – (14)
Solution :
Given, 99/144
√99/144 = √3 × 3 × 11/12 × 12
= 3/12 √11
= 1/4 × 3.317
= 0.829
Question no – (15)
Solution :
Given, 57/169
√57/169 = √57/13 × 13 √57/13
= 7.550/13
= 0.580
Question no – (16)
Solution :
Given, 101/169
√101/169 = √101/13 × 13
= √101/13
Question no – (17)
Solution :
Given, 13.21
√13.12 = √1321/100
= 1321/10
Question no – (18)
Solution :
Given, 21.97
√21.97 = √2197/√100
= √13 × 13 × 13/√10 × 10
= 13/10 √13 = 1.3 × 3 .606
= 4.6878
Question no – (19)
Solution :
Given, 110
√110 = √11 × 5 × 2
= 3.167 × 2.236 × 1.414
= 10.013
Question no – (20)
Solution :
Given, 1110
√1110
= √111 × 2 × 5
Question no – (21)
Solution :
Given, 11.11
√11.11
= √1111/√100
= √1111/10
Question no – (22)
Solution :
As per the question,
Area = 325 m²
∴ one side length,
= √325 = √5 × 5 × 13
= 5 √13
= 5 × 3.606
= 18.03 m
Therefore, the approximate length of one side of the field will be 18.03 m.
Question no – (23)
Solution :
Area of rectangle = Area of square
= 240 × 70
= 16800 m²
∴ One side of square,
= √16800 = √2 × 2 × 2 × 2 × 2 × 3 × 7 × 5 × 5
= 2 × 2 × 5 = √2 × 3 × 7
= 20 √42 = 20 × 6.481
= 129.62 m
Thus, the length of the side of a square will be 129.62 m.
Next Chapter Solution :
👉 Chapter 4 👈