Warning: Undefined array key "https://nctbsolution.com/maths-wiz-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Maths Wiz Class 8 Solutions Chapter 4 Playing with Numbers
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Maths Wiz Class 8 Math Book, Chapter 4, Playing with Numbers. Here students can easily find step by step solutions of all the problems for Playing with Numbers, Exercise 4A, 4B and 4C Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 4 solutions. Here in this post all the solutions are based on ICSE latest Syllabus.
Playing with Numbers Exercise 4A Solution :
Question no – (1)
Solution :
Let the original number be 10a + b
Given a + b = 12
also given,
10a + b = 6b
10a + 5b => a/b = 5/10 = 1/2 = k
∴ a + b = 12
=> k + 2k = 12
=> 3k = 12
=> k = 4
∴ a = k
and b = 2k
∴ The number is a = 4 and b = 8
Question no – (3)
Solution :
Let the original number be 10a + b
Given a – b = 6
The digits are revers so the number be = 10a + b
also given,
(10a + b) + (10b + a) = 110
=> 11a + 11a = 110
=> a + b = 10
=> 6 + b + b = 10
=> 6 + 2b = 10
=> 2b = 4
=> b = 2
∴ a = 6 + 2 = 82
Therefore, the number will be 82
Question no – (4)
Solution :
Let the original number be = 10a + b
Given, 10a + b = (a + b)8
The reverse number is = 10b + a
Also given, 10a + b – 45 = 10b + a
=> 9a – 9b = 45
=> a – b = 5
∴ a = 5 + b
10a + b = (a + b) 8
=> 10a – 8a + b – 8b = 0
=> 2a – 7b = 0
=> 10 + 2b – 7b = 0
=> 10 – 5b = 0
=> 5b = 10
=> b = 2
∴ a = 5 + b = 5 + 2 = 7
Therefore, the required number will be 72
Question no – (5)
Solution :
Let the original number be 100a + 10b + c right hand being zero
∴ The number become – 100a + 10b
The first condition
(100a + 10b) – (100b + 10) = 180
=> 90a – 90b = 180
=> a – b = 2
The second condition 100 × a/2 + 0 + b = 50a + b
and so, (100a + 10b) – (50a + b) = 454
=> 50a + 9b = 454
=> 50 × (2 + b) + 9b = 454
=> 100 + 50b + 9b = 454
=> 59b = 354
=> b = 6
∴ a – 6 = 2
a = 8
Therefore, the required number will be 860
Playing with Numbers Exercise 4B Solution :
Question no – (1)
Solution :
As we know, If the last digit of the number is 0, 2, 4, 6, and 8 then the number is divisible by 2.
Hence, 60, 216, 890, 992 are divisible by 2.
Question no – (2)
Solution :
We know, A number is divisible by 3 if the sum of digits is divisible by 3
Here, in the question the number is 24
So, 24 = 2 + 4 = 6
6 is divisible by 3
So, what can we say?
Yes, 24 is divisible by 3.
Thus, 24, 48, 105, 726, 915 are divisible by 3
Question no – (3)
Solution :
As we know, A number is divisible by 5 if the last digit of the given number is 0 or 5
Hence, in the question the number is 30 (last digit is 0)
So, it is divisible by 5
Therefore, 30, 210, 305, 640, 740, 985 are divisible by 5.
Question no – (4)
Solution :
We know, A number is divisible by 9 if the sum of all digits is divisible by 9
Here, in the question the number is 63
So, 63 =6 + 3 = 9
9 is divisible by 9
So, what can we say?
Yes, 63 is divisible by 9.
Hence, 63, 90, 243, 180, 936 are divisible by 9.
Question no – (5)
Solution :
We know, A number is divisible by 10 if its unit digit place is ‘0’
Here, in the question the number is 80 (whose last digit is 0)
So, 80 id divisible by 10
Thus, 80, 140, 400, 670, 990 are divisible by 10.
Playing with Numbers Exercise 4C Solution :
Question no – (1)
Solution :
(a) 563 582 620 677 753 848

∴ 848 + 114 = 962
(b) 17 17 51 255 1785 16065

∴ 16065 × 11 = 176715
Question no – (3)
Solution :
(d) 62 = 36
Question no – (4)
Solution :

The correct option will be – (a) 1, 2
Question no – (5)
Solution :
91 – 22 = 87
81 – 32 = 72
17 – 42 = 1
Therefore, the missing number is (a) 17
Question no – (7)
Solution :
Complete Magic Square :
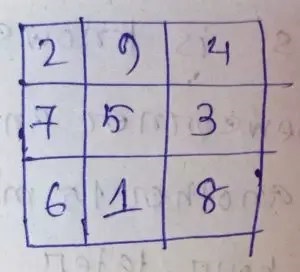
Question no – (8)
Solution :

Question no – (9)
Solution :
Required Magic Hexagon :
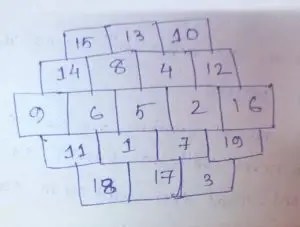
Question no – (16)
Solution :
9 + 9 + 9 / 9 + 9, 9 + 9 × 9/9 × 9, (9 + 9/9) × 9/9, 99/9 – 9/9, √9 + √9 + √9 + 9/9, many more combinations are possible.
Question no – (17)
Solution :
The clock takes 1.5 see between each strike.
(6 + 1.5) = 7.5 see it take to strike 6 O’clock.
Question no – (18)
Solution :
The smallest integer that can be written with two integer is 1
It can be written as = 2/2, 3/3 or 2°, 3°
Question no – (19)
Solution :
1 by using all the ten digits
We will have to present this as the sum of two tractions :
148/296 + 35/70 = 1
Question no – (20)
Solution :
10 with five 9s
= 9 + 99/99 = 10, 9 + 9+9/9+9 = 10, 9 + 9×9/9×9 = 10, 99/9 – 9/9 = 10
Question no – (21)
Solution :
100 by using all the ten digits,
70 + 24 9/18 + 5 3/6 = 100
80 27/54 + 19 3/6 = 100 ; 87 + 9 4/5 + 3 12/60 = 100
50 1/2 + 49 38/76 = 100
Question no – (22)
Solution :
Four different ways of writing 100 with five identical digits,
(i) 111 – 11 = 100,
(ii) 5 × 5 × 5 – 5 × 5 = 100,
(iii) 33 × 3 + 3/3 = 100,
(iv) (5 + 5 + 5 + 5) × 5 = 100
Question no – (23)
Solution :
The biggest number can be written with four 1’s = 1111
Next Chapter Solution :
👉 Chapter 5 👈