Warning: Undefined array key "https://nctbsolution.com/maths-ace-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Maths Ace Class 8 Solutions Chapter 14 Mensuration
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Maths Ace Prime Class 8 Math Book, Chapter 14, Mensuration. Here students can easily find step by step solutions of all the problems for Mensuration, Exercise 14.1, 14.2, 14.3, 14.4 and 14.5 Also here our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 14 solutions.
Mensuration Exercise 14.1 Solution :
Question no – (1)
Solution :
If we add a circle right ,of park A then it equals of park ’B’
∴ Park ‘B’ has greater area
So, the area of circle,
= 32/7 × 15 × 15
= 706.5 m2
Therefore, Park B has greater area.
Question no – (2)
Solution :
Let, side of one square x cm and the side of another square (x + 5) cm
∴ (x + 5)2 – (x2) = 325
= x2 + 10x + 25 – x2 = 325
= 10x = 325 – 25
= x = 300/10
= 30
∴ Side of one square 30 cm and another side square,
= (30 + 5) cm
= 35 cm.
Question no – (3)
Solution :
According to the question,
∴ Area of floor,
= (8.4 × 5.4) cm2
= 45.36 m2
= 453600 cm2
∴ Area of marble pieces –
= 1/2 × 40 × 30
= 600 cm2
∴ No of marble piece required,
= 453600/600
= 750 marble piece
Question no – (4)
Solution :
Area of rectangular lawn,
= (80 × 60) m2
= 4800 m2
∴ Total cost,
= (4800 × 7.5) Rs
= 36000 Rs
Therefore, the cost of levelling the lawn is 36000 Rs.
Question no – (5)
Solution :
Area of square,
= (35)2
= 1225 m2
Area of rectangle
= (51 × 25) m2
= 1275 m2
∴ Total area,
= (1225 + 1275) m2
= 2500 m2
Area of new square field = 2500 m2
∴ Let side, ‘S’
∴ S × S = 2500
= s2 = 2500
= s = 50 m
Therefore, Side of the square field = 50 m.
Question no – (6)
Solution :
Area of path on length wise,
= (125 – 3) × 5
= 610 m2
And, area of path on breadth wise,
= (125 – 5) × 3
= 360 m2
∴ Area of path of intersection,
= 5 × 3
= 15 m2
∴ Area of two pathways,
= (610 + 360 + 15)
= 985 m2
Question no – (7)
Solution :
As per the given question,
The area of a parallelogram is 780 sq. cm.
If the length of one side is 26 cm
∴ The corresponding height,
= 780/26
= 30 cm
Hence, the corresponding height will be 30 cm.
Question no – (8)
Solution :
In the give question,
One side of a parallelogram is = 15 cm,
The area is = 375 sq. cm
Let, length of side x cm,
∴ x × 15 = 375
= x = 375/15
= 25 cm
Therefore, The Length of attitude will be 25 cm.
Question no – (9)
Solution :
In the question we get,
The base and height of a triangle are in the ratio 4 : 5.
The area is 640 sq. cm,
Let, base is 4x and height 5x
∴ 1/2 × 4x × 5x = 640
= 10x2 = 640
= x2 = 64
= x = 8
∴ Base = (4 × 8) = 32 cm
∴ height = (5 × 8) = 40 cm
Therefore, the base is 32 cm and height is 40 cm.
Question no – (10)
Solution :
As we know, Area = 1/2 × base × height
∴ 3136 = 1/2 × B × 64
= 3136 = 32 B
= B = 3136/32
= 98 cm
Therefore, the Base is 98 cm.
Question no – (11)
Solution :
In the given question,
The base of a parallelogram is 12 cm and its height is 18 cm
∴ Area of parallelogram,
= (12 × 18) cm2
= 216 cm2
Therefore, the area of parallelogram is 216 cm2
Question no – (12)
Solution :
According to the question,
Area of ABCD,
= (10 × 12 + 20 × 12)
= 120 + 240
= 360 cm2 – 120 cm2
= 240 cm2
Therefore, the area of parallelogram ABCD is 240 cm2
Mensuration Exercise 14.2 Solution :
Question no – (1)
Solution :
As per the question we get,
The lengths of parallel sides of a trapezium are = 20 cm and 14 cm.
The distance between them is = 10 cm
∴ Area of trapezium,
= 1/2 × (20 + 14) × 10
= 1/2 × 34 × 10
= 170 cm2
Thus, the area of the trapezium will be 170 cm2
Question no – (2)
Solution :
According to the given question,
The area of a rhombus is = 225 sq. cm.
The length of one of its diagonals is = 15 cm
∴ Area = 1/2 × d1 × d2
= 225 = 1/2 × 15 × d2
= d2 = 225 × 2/15
= d2 = 30 cm
Thus, the length of the other diagonal will be 30 cm.
Question no – (3)
Solution :
As per the question,
One side is equal to = 10 cm
The length of one of the diagonals is = 12 cm
∴ The Area rhombus,
= 1/2 p √4a2 – p2
= 1/2 × 12 √4 × 102 – 122
= 6 √400 – 144
= 6 × √256
= 6 × 16
= 96 cm
Therefore, the area of rhombus will be 96 cm.
Question no – (4)
Solution :
According to the given question,
Diagonals of a rhombus are 16 cm and 30 cm
∴ Area of rhombus,
= (1/2 × 16 × 30)
= 240 cm2
∴ Length of side,
= √d12 + d22/2
= 162 + 302/2
= √256 + 900/2
= √1156/2
= 17 cm
Hence, the area will be 240 cm2 and the length of the side will be 17 cm.
Question no – (5)
Solution :
Let, sides are 4x and 5x
∴ 1/2 × (4x + 5x) × 12 = 54
= 1/2 × 9x × 12 = 594
= x = 594 × 2/12 × 9
= x = 11 cm
∴ Parallel sides are,
= (4 × 11) = 44 cm
= (5 × 11) = 55 cm
Therefore, the lengths of the parallel sides are 44 cm and 55 cm.
Question no – (6)
Solution :
Let, sides x and 2x
∴ 1/2 × (x + 2x) × 24 = 900
= 1/2 × 3x × 24 = 900
= 36x = 900
= x = 900/36
= 25 cm
∴ Two parallel sides are,
= 25 cm and
= (25 × 2)
= 50 cm
Therefore, the length of the two parallel sides are 25 cm and 50 cm.
Question no – (7)
Solution :
As per the question we know,
The area of a rhombus is = 966 sq. cm.
length of one of its diagonals is = 46 cm,
∴ Area of rhombus,
= 1/2 × (d1 × d2)
= 966 = 1/2 × (46 × d2)
= 46 d2 = 966 × 2
= d2 = 966 × 2/46
= 42 cm
Therefore, the length of the other diagonal is 42 cm
Question no – (8)
Solution :
1st, Area of triangle,
= (1/2 × 48 × 16) m2
= 384 m2
2nd, Another area,
= (1/2 × 48 × 26) m2
= 624 m2
Now, the total area,
= (624 + 384) m2
= 1008 m2
Therefore, area of the field will be 1008 m2
Question no – (9)
Solution :
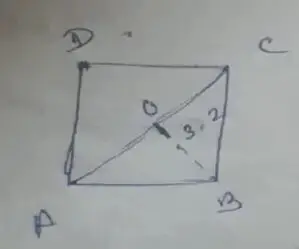
Here, Area = 23.36 sq.cm
Let AC = x
OB = 3.2 cm
By question 1/2 × b × h = 23.36/2
= 1/2 × 3.2x = 11.68
= 1.6x = 11.68
= x = 11.68/1.6
= 7.3 cm
∴ AC = 7.3 cm.
Question no – (10)
Solution :
In the given question we get,
lengths of the two diagonals of the hall are = 12 m and 16 m
The rate of painting = Rs 6.50 per sq. m
∴ Area of rhombus,
= (1/2 × 12 × 16) m2
= 96 m2
∴ Total cost of painting the floor of the rate 6.50 Rs,
= (6.50 × 96) Rs
= 624 Rs
Therefore, the cost of painting the floor will be 624 Rs,
Mensuration Exercise 14.3 Solution :
Question no – (1)
Solution :
From figure – (a)
Area of ABCDE = Area of △ABC × Area of △ACD × Area of △AED
In right angle, △ADC
AC2 = CD2 + AD2
= 122 + 52
= 144 + 25
= 169
∴ AC = 13 cm
∴ Area of △ABC
= (1/2 × 13 × 5.5)
= 35.75 cm2
∴ Area of △ADC
= 1/2 × 12 × 5
= 30 cm2
Area of △AED
= (1/2 × 12 × 4.5) cm2
= 27 cm2
Total area,
= (35.75 + 30 + 27) cm2
= 92.75 cm2
From figure – (b)
Area of ABCDEFGH
= Area of ABG + Area of parallelogram CDEF + Area of trapezium BCFG
∴ Area of △ABG = (1/2 × 10 × 3)
= 15 cm2
Area of trapezium BCFG,
= 1/2 × 5 × (10 + 6)
= 1/2 × 5 × 16
= 40 cm2
Area of parallelogram CDEF,
= (6 × 4.5) cm2
= 27 cm2
∴ Total area,
= (15 + 40 + 27) cm2
= 82 cm2
Question no – (2)
Solution :
First, Area of floor,
= (25 × 20) m2
= 500 m2
= 5000000 cm2
Now, Area of rhombus,
= (25 × 10) cm2
= 250 cm2
∴ No of tiles,
= 5000000/250
= 20000 tiles
Therefore, the number of tiles required will be 20000 tiles.
Question no – (3)
Solution :
As per the given figure,
Area of grass portion,
= (22 × 10) m2
= 220 m2
Area of flower bed = Area of trapezium ABGH + Area of trapezium DEFG
Now, Area of trapezium,
= 1/2 × 8 × (10 + 22) + 1/2 × (8) (10 + 22)
= (128 + 128) m2
= 256 m2
∴ Total area,
= (220 + 256) m2
= 476 m2
Therefore, the area of the trapezium will be 476 m2
Mensuration Exercise 14.4 Solution :
Question no – (1)
Solution :
(a) As per the question we know,
length = 14 cm,
breadth = 10 cm
height = 9 cm.
As we know, Total Surface area = 2 (l×b + bh + l×h)
∴ Total surface area,
= 2 (lb + bh + hd)
= 2 (14 × 10 + 10 × 9 + × 14) cm2
= 2 (140 + 90 + 126) cm2
= 2 × 356
= 712 cm2
Therefore, the surface area of the cuboid will be 712 cm2
(b) According to question we know,
Length = 16 cm,
Breadth= 12 cm
Height = 7 cm
As we know, Total Surface area = 2 (l × b + b × h + l × h)
∴ Total surface is,
= 2 (16 × 12 + 12 × 7 + 7 × 16) cm2
= 2 (192 + 84 + 112) cm2
= (2 × 388)cm2
= 776cm2
Hence, the surface area of the cuboid wise776cm2
(c) In the given question,
Length = 24 cm,
Breadth = 20 cm
Height = 15 cm
As we know, Total Surface area = 2 (l × b + b × h + l × h)
∴ Total Surface area,
= 2 (24 × 20 + 20 × 15 × 24)
= 2 (480 + 300 + 360)
= (2 × 1140)
= 2280cm2
Thus, the surface area of the cuboid is 2280cm2
Question no – (2)
Solution :
As per the question we know,
length = 400 cm = 4 m
breadth = 220 cm = 2 m 20 cm
Height = 120 cm = 1.20 m
As we know, Total Surface area = 2 (l × b + b × h + l × h)
∴ Surface area,
= 2 (4 × 2.20 + 2. 20 × 1.20 + 1.20 × 4)
= 2 × 98.80 + 2.64 + 4.80)
= 32.48 m2
Now, Cost of polishing,
= (32.48 × 24) Rs
= 779.52 Rs
Therefore, the cost of polishing the box will be 779.52 Rs.
Question no – (3)
Solution :
Given, Lateral surface area = 64m2
= 4x2 = 64
= x2 = 16
= x = 4
∴ Total surface area,
= 6 × 42
= 6 × 16
= 96 m2
Therefore, the total surface area of the cube is 96 m2
Question no – (4)
Solution :
First, Area of the room,
= 2 (8 + 6) × 4
= 2 × 14 × 4
= 112 sq.m
∴ Cost of point,
= (112 × 80)
= 8960 Rs.
Therefore, the cost of paint required will be 8960 Rs.
Question no – (5)
Solution :
Length = breadth …..(according to the question)
∴ Total surface area = 120
= 2 (lb + bh + hl) = 120
= (lb + bh + hl) = 60
= (x2 + 2x + 2x) = 60
= x2 + 4x = 60
= x2 + 4x – 60 = 0
= – 10 + 6
∴ x = 6
= L b = 6
Therefore, the Length is 8 m breadth 6 m.
Question no – (6)
Solution :
First, Area of four walls,
= 2 (8 + 4) ×
= 2 × 12 × 2
= 48 m2
∴ Number of blue tiles required,
= 48/1.5
= 32 tiles
∴ Number of Area of floor,
= (8 × 4) m2
= 32 m2
∴ Number of white tiles required,
= 32/2
= 16 tiles
Mensuration Exercise 14.5 Solution :
Question no – (1)
Solution :
(a) As per the question we know,
Length = 13 m,
Breadth = 10 m
Height = 5 m
As we know, Volume of cuboid = (l × b × h)
∴ Volume of cuboid,
= (13 × 10 × 5) m3
= 650 m3
Therefore, the volume of a cuboid will be 650 m3
(b) According to the question,
length = 0.5 m,
breadth = 0.3 m
depth = 0.02 m
As we know, Volume of cuboid = (l × b × h)
∴ Volume of cuboid,
= (0.5 × 0.3 × 0.02)m3
= 0.003 m3
Therefore, the volume of a cuboid will be 0.003 m3
(c) Given in the question,
length = 8 m,
breadth = 6 m
depth = 3 m.
As we know, Volume of cuboid = (l × b × h)
∴ Volume of the cuboid,
= (8 × 6 × 3) m3
= 144m3
Therefore, the volume of a cuboid will be 144m3
Question no – (2)
Solution :
Let, breadth x m
∴ (8 × 6 × x) = 200 (….according to the question)
= x = 200/48
= 4.17 m
Therefore, the Breadth will be 4.17 m.
Question no – (3)
Solution :
As we know, Volume of cube of edge = (x × x × x) = x3
∴ Volume of cube,
= (10 10 × 10) cm3
= 100 cm3
= 1L
Question no – (4)
Solution :
According to question we know,
Cartons each having length 2.4 m, breadth 1.4 m and height 0.8 m.
Room of dimensions = 6 m × 7m × 8 m
∴ Number of cartoons,
= 6 × 7 × 8/1.4 × 1.4 × 0.8
= 125 cartoons
Therefore, the number of cartons will be 125.
Question no – (5)
Solution :
Let, the sides are, 2x 3x, 5x
∴ 2.x × 3x × 5x = 21870
= 30x3 = 21870
= x3 = 21870/30
= 729
= x = 9
∴ Sides are,
= (2 × 9) = m = 18m
= (3 × 9) = 8T m = 27
= (5 × 9) m. 45m
∴ Total surface area,
= 2 (18 × 27 + 27 × 45 + 45 × 18) m2
= 5022 m2
Therefore, total surface area of the cuboid is 5022 m2
Question no – (6)
Solution :
Given in the question,
radius = 1.4 m
height = 10 m
∴ Volume of well = πr2h
= 22/7 × 1.4 × 1.4 × 10
= 61.6m3
Therefore, the quantity of soil that had been taken out 61.6m3
Question no – (7)
Solution :
As per the question we know,
Radius = 13/2 m = 6.5 m
Depth = 35 m
∴ Volume of drum = πr2h
= 22/7 × 6.5 × 6.5 × 35
= 4647.5 m3
Now, half of the volume of drum,
∴ Volume of water,
= 4647.5/2m3
= 2323.75 m3
Therefore, the volume of the water inside the drum will be 2323.75 m3
Question no – (8)
Solution :
According to the given question,
Inner and outer walls of a 30 cm long pipe have a diameter of 15 cm and 17 cm,
∴ Volume of the material used in pipe,
= π× h × (R2 – r2)
= 22/7 × 30 ((17/2)2 – 915/2)2)
= 22/7 × 30 (8.52 – 7.52)
= 22/7 × 30 × (8.5 + 7.5) (8.6 – 7.5)
= 22/7 × 30 × 16 × 1
= 1508.5 m3
Therefore, the volume of the materials will be 1508.5 m3
Question no – (9)
Solution :
As per the question,
Diameter = 8 ft
radius = 4 ft
∴ Cost of painting,
= (20 × 2 × 22/7 × 4 × 14/2.5)
= 2816 Rs.
Therefore, the cost of painting the inner wall of a well 2816 Rs.
Question no – (10)
Solution :
Height = 3m = 300 cm
Circumference = 252
∴ 2πr = 252
= 2 × 22/7 × r = 252
= r = 252 × 7/44
= 40.09 cm
Now, lateral surface area,
= 2πrh = 2 × 22/7 40.09 × 300
= 75600 cm2
Therefore, the lateral surface area will be 75600 cm2
Question no – (11)
Solution :
According to the question we know,
r = 0.5/2 m
∴ Total curved surface area,
= 2 × 22/7 × 0.5/2 × 1.5
= 33/14 sqm
∴ Number of revolutions,
= 264/33/14
= 264 × 14/33
= 112 revolutions
Therefore, it will take 112 revolutions.
Question no – (12)
Solution :
In the given question,
Rectangular piece of paper having length 4.4 cm and breadth 1.5 cm
First, the height,
= 2πr = 4.4
= r = 4.4 × 7/2 × 22
= 0.7 cm
Now, the Volume,
= (22/7 × 0.7 × 0.7 × 1.5)
= 2.310cm3
Therefore, the height will be 0.7 cm and the volume will be 2.310cm3
Next Chapter Solution :
👉 Chapter 15 👈