Warning: Undefined array key "https://nctbsolution.com/frank-icse-mathematics-class-8-solutions/" in /home/862143.cloudwaysapps.com/hpawmczmfj/public_html/wp-content/plugins/wpa-seo-auto-linker/wpa-seo-auto-linker.php on line 192
Frank ICSE Mathematics Class 8 Solutions Chapter 6 Sets
Welcome to NCTB Solutions. Here with this post we are going to help 8th class students for the Solutions of Frank ICSE Mathematics Class 8 Math Book, Chapter 6, Sets. Here students can easily find step by step solutions of all the problems for Sets, Exercise 6.1, 6.2 and 6.3 Also our mathematics teacher’s are solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 6 solutions. Here in this post all the solutions are based on latest Syllabus.
Sets Exercise 6.1 Solution :
Question no – (1)
Solution :
(a) All tall boys in your class
= No, because information is not well-defined
(b) Collection of clever students in your class
= No, because information is not well-defined
(c) Collection of cars belonging to the people of Lucknow
= Yes, it is a set.
(d) Collection of all students of your school who are interested in maths
= No, because information is not well-defined
(e) Collection of all teenagers in your colony.
= Yes, it is a set.
(f) Collection of all interesting books in your school library
= No, because information is not well-defined.
(g) Collection of present members of the Lok Sabha of India.
= Yes, it is a set.
(h) Collection of all polygons having at least t sides
= Yes, it is a set.
(i) Collection of people of India who are overweight
= No, because information is not well-defined.
(j) Collection of grandparents of students of your class
= Yes, it is a set.
Question no – (2)
Solution :
Before we solve the above questions, first we need to understand what is Roster and Set builder method,
Roster method : In this method all the elements are written or listed one after the other using commas, without repetition inside curly brackets.
Set builder method : In this method, the property which describes the elements of the set is mentioned.
(a) {The days of the week}
Roster : A = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
Set builder : A = {x : x is a day of the week}
(b) {Vowels of the English alphabets}
Roster : B = {a, e, i, o, u},
Set builder : B = {x : x is a vowel}
(c) {Factors of 24}
Roster : C = {1, 2, 3, 4, 6, 12, 24},
Set builder : C = {x : x | 24}
(d) {Composite natural numbers between 80 and 100}
Roster : D = {81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99}
Set builder : D = {x : x ∈ N, x is a composite number, 80 < x < 100}
Question no – (3)
Solution :
Before we solve the given problem, first we need to understand what is descriptive method,
Descriptive Method : In this method, a well defined description of the element of the set is written inside curly brackets.
(a) A = {January, March, May, July, August, October, December}
Descriptive form :A = {January, March, May, July, August, October, December}
(b) B = {a, e, i, o, u}
Descriptive form :B = {a, e, i, o, u}
(c) P = {Sunday, Monday, Friday}
Descriptive form 😛 = {Sunday, Monday, Friday}
(d) S = {100, 121, 144, 169, 196}
Descriptive form : S = {100, 121, 144, 169, 196}
(e) L = {a, l, g, e, b, r}
Descriptive form : L = {a, l, g, e, b, r}
(f) R = {Ganga, Yamuna, Brahmaputra, Godavari, Narmada, Cauvery, Mahanadi, Krishna}
Descriptive form : R = {Ganga, Yamuna, Brahmaputra, Godavari, Narmada, Cauvery, Mahanadi, Krishna}
(g) A = fish, shark, whale, crocodile, alligator}
Descriptive form : A = fish, shark, whale, crocodile, alligator}
(h) B = {Delhi, Kolkata, Chennai, Mumbai}
Descriptive form : B = {Delhi, Kolkata, Chennai, Mumbai}
Question no – (4)
Solution :
(a) A = {x : x = n3, n ≤ 7, n ∈ W}
In roster form,
= A = {0, 1, 8, 27, 64, 125, 216, 343}
(b) B = {x : x is letter of the word ‘abracadabra’}
In roster form,
= B = {a, b, r, c, d}
(c) R = {x : x ∈ N, 9 < x < 99 and sum of digits of x = 7}
In roster form,
= R = {16, 25, 34, 43, 52, 61}
(d) C = {x : x = n2 – 1, x < 25, n ∈ W}
In roster form,
= C = {-1, 0, 3, 8, 15, 24}
(e) D = {x : x = 5n, n ∈ N, n ≥ 20}
In roster form,
= D = {100, 105, 110, 115, ….}
(f) E = {x : x = n/n + 1, n ∈ N}
In roster form,
= E = {1/2, 2/3, 3/4, 4/5, ….}
(g) F = {x : x is a factor of 72}
In roster form,
F = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}
(h) G = {x : x ∈ Z, -7 ≤ x < 7}
In roster form,
= G = {-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
(i) P = {x : x is a vowel in the word ‘aerobics}
In roster form,
= P = {a, e, i, o}
(j) Q = {x : x = 7n – 3, n ∈ N and n < 9}
In roster form,
= Q = {4, 11, 18, 25, 32, 39, 46, 53}
Sets Exercise 6.2 Solution :
Question no – (1)
Solution :
(a) A = {x : x ∈ Z, 0, < x < 1}
= It is empty set.
(b) B = {set of all natural satellites of the earth}
= It is singleton set.
(c) X = {set of all women prime ministers of India}
= It is singleton set.
(d) Y = {set of vowels in the word ‘follow’}
= It is singleton set.
(e) P = {set of vowels not in the word ‘Constantinople’}
= It is singleton set.
(f) Q = {x : x ∈ N and x is a multiple of 11 between 100 and 110}
= It is singleton set.
(g) A = {x : x ∈ Z, -1 < x < + 1}
= It is singleton set.
(h) B = (set of vowels not in word equatorial}
= It is singleton set.
(i) C = {x : x ∈ N and x is prime number, 23 < x < 29}
= It is empty set.
Question no – (2)
Solution :
(a) A = {x : x ∈ N, x ≤ 7}; B = {x : x ∈ W, x < 7}
= A = {1, 2, 3, 4, 5, 6, 7};
= B = {0, 1, 2, 3, 4, 5, 6}
∴ Equivalent sets.
(b) A = {set of letters of the word match};
B = {set of letters of the word March}
= Equivalent sets.
(c) A = {x : x = n2, n ∈ N, n < 8}; B = {set of all perfect squares less than 50}
= A = {1, 4, 9, 16, 25, 36, 49};
= B = {1, 4, 9, 16, 25, 36, 49}
∴ Equal sets.
(d) A = {set of all odd natural numbers less than 12}; B = {set of all 2-digit prime numbers less than 30}
= A = {1, 3, 5, 7, 9, 11};
= B = {11, 13, 17, 19, 23, 29}
∴ Equivalent sets.
Question no – (3)
Solution :
(a) A = {x : x ∈ N, x ≤ 7}; B = {x : x ∈ W, x < 7}
= A = {1, 2, 3, 4, 5, 6, 7};
= B = {0, 1, 2, 3, 4, 5, 6}
∴ Equivalent sets.
(b) A = {set of letters of the word match};
B = {set of letters of the word March}
= Equivalent sets.
(c) A = {x : x = n2, n ∈ N, n < 8}; B = {set of all perfect squares less than 50}
= A = {1, 4, 9, 16, 25, 36, 49};
= B = {1, 4, 9, 16, 25, 36, 49}
∴ Equal sets.
(d) A = {set of all odd natural numbers less than 12}; B = {set of all 2-digit prime numbers less than 30}
= A = {1, 3, 5, 7, 9, 11};
= B = {11, 13, 17, 19, 23, 29}
∴ Equivalent sets.
Question no – (5)
Solution :
(a) A = {x : x ∈ N and x is 1-digit prime number}
= A = {2, 3, 5, 7}
∴ No of subsets = 24 = 16
(b) B = {set of all months of the year starting with the letter J}
= B = {January, June, July}
∴ No of subsets = 23 = 8
(c) C = {set of the first 4 multiples of 5}
= C = {5, 10, 15, 20}
∴ No of subsets = 24 = 16
(d) D = {set of letters of the word school}
= D = {s, c, h, o, l}
∴ No of subsets = 25 = 32
Sets Exercise 6.3 Solution :
Question no – (1)
Solution :
A = {45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55}
B = {46, 48, 50, 52, 54},
C = {45, 48, 51, 54, 57}
Therefore,
(a) A ∪ B = {45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55} = A
(b) A ∩ B = {46, 48, 50, 52, 54} = B
(c) A ∩ C = {45, 48, 51, 54} = C – {57}
(d) A ∪ C = {45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 57} = A ∪ {57}
(e) A – C = {46, 47, 49, 50, 52, 53}
(f) C – A = {54}
Question number – (2)
Solution :
According to the question,
X = {1, 2, 3, 4, 6, 12, 18, 24, 36, 72}
Y = {1, 2, 3, 6, 9, 18, 27, 54}
Z = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
Therefore,
(a) X ∪ Y = {1, 2, 3, 4, 6, 9, 12, 18, 24, 27, 36, 54, 72}
(b) Y ∩ Z = {1, 2, 3, 6}
(c) X – Y = {4, 12, 24, 36, 72}
(d) X ∩ Y ∩ Z = {1, 2, 3, 6}
Question no – (3)
Solution :
(a) Given in the question,
ξ = {1, 2, 3, 4, 5};
A = {2, 4}
Therefore,
A1 = ξ – A = {1, 3, 5}
(b) According to the question,
A = {2, 3, 5, 6},
B = {1, 3, 7, 11, 12}
C = {6, 12}
Therefore, B ∪ C = {1, 3, 6, 7, 11, 12}
(B ∪ C) ∩A = {1, 3, 6, 7, 11, 12} ∩ {2, 3, 5, 6} = {6}
Question no – (4)
Solution :
According to the question,
ξ = {5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
X = {11, 12, 13, 14, 15, 16, 17, 18, 19}
Y = {1, 2, 3, 4, 5, 6, 7, 8, 9}
(a) X ∪ Y = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19}
∴ n(X ∪ Y) = 18
(b) X∩Y = φ
∴ n(X ∩ Y) = 0
(c) X1 = {5, 6, 7, 8, 9, 10, 20}
∴ n(X1) = 7
(d) (X ∪ Y)1 = {20}
∴ n(X ∪ Y)1 = 1
(e) (X – Y) = X, Since n(X ∩ Y) = 0
∴ n(X – Y) = n(X) = 9
Therefore,
L.H.S. > n(X ∪ Y) = 18
R.H.S. > n(X) + n(Y) – n(X ∩ Y) = 9 + 9 – 0 = 18
Sets Exercise 6.4 Solution :
Question no – (1)
Solution :
(a) Given, A, B, C
A = {1, 3, 5, 7, 11, 13}
B = {2, 4, 6, 8, 10, 12}
C ={1, 2, 3, 4, 5, 6}
(b) Given, (A ∩ C) ∪ (B ∩ C)
∴ (A ∩ C) ∪ (B ∩ C)
= {2, 3, 5} ∪ {2, 4, 6}
= {2, 3, 4, 5, 6}
(c) Given, A ∩ B ∩ C
∴ A ∩ B ∩ C = {2}
(d) Given, A – B
∴ A – B = {3, 5, 7, 11, 13}
(e) Given, B – C
∴ B – C = {8, 10, 12}
(f) Given, A ∩ B
∴ A ∩ B = {2}
(g) Given, n(A ∪ B ∪ C)
= A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13}
∴ n(A ∪ B ∪ C) = 12
(h) Given, n(ξ)
= ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
∴ n(ξ) = 13
Question no – (2)
Solution :
Required Venn diagram :
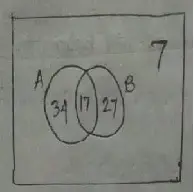
Therefore,
(a) n(A ∪ B)
= n(A ∪ B)
= 34 + 17 + 27
= 78
(b) n(A – B)
= n(A – B)
= 34
(c) n(B – A)
= n(B – A)
= 27
(d) n(A ∪ B)1
= n(A ∪ B)1
= 7
Question no – (3)
Solution :
Required Venn diagram :
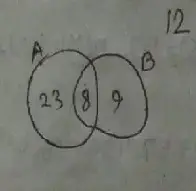
According to the question,
n(ξ) = 52
n(A) = 31
n(B) = 17
n(A ∩ B) = 8.
Therefore,
(a) n(A ∪ B)
= n(A ∪ B)
= 23 + 8 + 9
= 40
(b) n(A1)
= n(A1)
= 52 – 31
= 21
(c) n(A ∪ B)1
= n(A ∪ B)1
= 52 – 40
= 12
Question no – (4)
Solution :
Required Venn diagram :
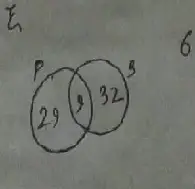
According to the question,
n(A) = 29,
n(B) = 27,
n(A ∪ B) = 47
Therefore,
(a) n(A ∩ B)
= n(A ∩ B)
= 9
(b) n(A – B)
= n(A – B)
= 20
Question no – (5)
Solution :
Required Venn diagram,
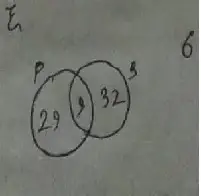
From the question we get,
n(A) = 38
n(Q) = 41
n(P ∩ Q) = 9
n(P ∪ Q) = 6
Therefore, the value of n(ξ),
= n(ξ)
= 29 + 9 + 32 + 6
= 76
Question no – (6)
Solution :
Required Venn diagram :
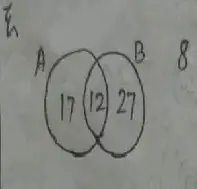
According to the question,
n(P) = 64
n(A) = 29
n(A ∪ B)’ = 8
n(A ∩ B) = 12
Therefore, (a) n (B)
= n(B) = 64 – (17 + 8)
= 64 – 25
= 39
(b) n (B – A)
= n(B – A)
= 27
(c) n(B)
= n(B)1
= 64 – 39
= 25
Question no – (7)
Solution :
Required Venn diagram,
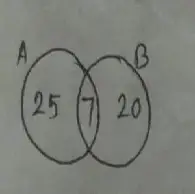
From the question we get,
n(A – B) = 25
n(B – A) = 20
n(A ∪ B) = 52
Therefore,
(a) n(B)
= n(A∩B)
= 52 – (25 + 20)
= 52 – 45
= 7
(b) n(A)
= n(A)
= 25 + 7
= 32
(c) n(B)
= n(B) = 20 + 7
= 27
Question no – (8)
Solution :
According to the question,
ξ = {set of all quadrilaterals)
A = {set of all parallelograms)
B = {set of all rectangles)
C = {set of all rhombuses)
Required Venn diagram,
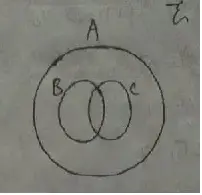
The type of quadrilateral which belongs to BC.
= Squares will belong to B ∩ C.
For any doubt please comment in the comment section.
Question no – (9)
Solution :
Required Venn diagram :
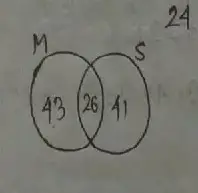
Therefore,
n(M) = 69,
n(S) = 57,
n(M∪S) = 124 – 24 = 100
Now,
∴ n(M ∩ S)
= 69 + 57 – 100
= 26
(a) Only in maths
= n(M) = 43,
(b) only in science
n(S) = 41,
(c) both in maths and science
n(M∩S) = 26
Question number – (10)
Solution :
Required Venn diagram,
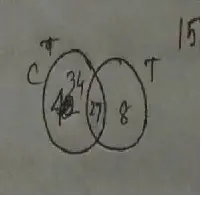
∴ n(C ∪ T) = 84 – 15 = 69
∴ n(C – T) = 61 – 27 = 34
∴ n(T – C) = 69 – (34 + 27)
= 69 – 61
= 8
(a) the number of students who like tennis.
= n(T)
= 27 + 8
= 35
(b) the number of students who like only one of the games.
= n[(C ∪ T) – (C ∩ T)
= 34 + 8
= 42
Question no – (11)
Solution :
Let,
A ≡ set readers of “The Times of India”
B ≡ set of readers of “The Hindu”
∴ n(A) = 72, n(B) = 56, n(A∪B)1 = 7, n(ξ) = 120
(a) Read both of them,
= n(A∩B) = [n(A) + n(B)] – [n(ξ) – n (A ∪B) ]
= [72 + 56] – [120 – 7]
= 128 – 113
= 15
(b) Read only The Times of India,
= n (A – B) = n (A) – n (A ∩ B)
= 72 – 15
= 57
(c) Read only The Hindu,
= n (B – A) = n (B) – n (A ∩ B)
= 56 – 15
= 41
Question no – (12)
Solution :
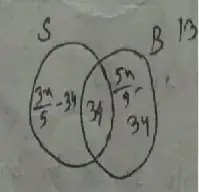
Let, S ≡ set of members who like swimming.
B ≡ set of members who like badminton.
Let x be the number of members of the club
According to the diagram,
= 3x/5 – 34 + 34 + 5x/9 – 34 + 13 = x
or, 3x/5 + 5x/9 – x = 21
or, 27x + 25x – 45x/45 = 21
or, 7x/45 = 21
or, x = 135
Therefore,
(a) the number who like only swimming.
= 3 × 135/5 – 34
= 81 – 34
= 47
(b) the number who like only badminton.
= 5 × 135/9 = 34
= 75 – 34
= 41
(c) the total number of members of the club.
= 135
Question no – (13)
Solution :
Let, S ≡ set of students opt for science
E ≡ set of students opt for economics
(a) Students enrolled for Science only?
= no of students enrolled for science only
= n (ξ) – n(E)
= 400 – 250
= 150
(b) Students enrolled for Economics only?
= no of students enrolled for economics only
= n (E) – n(Ens)
= 250 – 160
= 90
Question no – (14)
Solution :
(a) Number of people who drink both tea and coffee
= (25 + 20) – 40
= 45 – 40
= 5
(b) Number of people who drink only tea,
= 40 – 20
= 20
Question no – (15)
Solution :
Required Venn diagram,
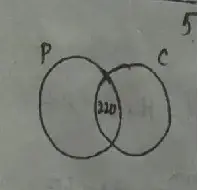
Since, 5% students failed in both Students
= P ∪ C = 100 – 5
= 95%
Now,
P ∩ C = {(70 + 80) – 95}% = 55%
∴ 55% = 220 ⇒ 100% = 400
Therefore, 400 candidates appeared for the examination.
Question no – (16)
Solution :
Since, 28 students speak English, and 20 Speak only English,
Therefore,
(a) students speak both Languages.
= 28 – 20
= 8
(b) Total students in the class.
= Number of students in the class = number of students who speak Hindi + number of students who speak only English
∴ 40 + 20
= 60
Question no – (17)
Solution :
(a) Number of students who play only football,
= no of students who play football – no of students who play both
= 200 – 70
= 130
(b) Number of students who play only cricket,
= 150 – 70
= 80
Question no – (18)
Solution :
(a) P, Q, R
= P = {a, b, c, d, e)}
= Q = {a, e, i, o, u}
= R = {d, e, f, g, h, i}
(b) P – Q
= P – Q
= {b, c, d}
(c) Q – R
= Q – R
= {a, o, u}
(d) P ∩ Q ∩ R
= P ∩ Q ∩ R
= {e}
(e) (P ∪ Q ∪ R)
= (P ∪ Q ∪ R)
= {k}
(f) (P ∩ Q) ∪ ( Q ∩ R) ∪ (P ∩ R)
= {a, e} ∪ {e, i} ∪ {d, e)}
= {a, e, d, i}
Next Chapter Solution :
👉 Chapter 7 👈