NCTB Class 8 Math Chapter Nine Exercise 9 Solutions by Math Expert. Bangladesh Board Class 8 Math Solution Chapter Nine Pythagoras Theorem Exercise 9 Solution.
|
Board |
NCTB |
| Class |
8 |
|
Subject |
Mathematics |
| Chapter |
9 |
|
Chapter Name |
Pythagoras Theorem |
| Exercise |
9 Solution |
Exercise 9
1> ABC is a right angled triangle. AD is the perpendicular to BC. Prove that, AB2+ BC2 + CA2= 4AD2
Ans:

Therefore, AB2+BC2+CA2 = 4AD2
2> Two diagonals of the quadrilateral ABCD intersect each other at right angled. Prove that, AB2 + CD2 = BC2 + AD²
Ans: 
3> In ꕔ ABC, ∠A is a right angle and CD is a median. Prove that, BC2 = CD² + 3AD2
Ans:
5> Prove that, the area of square region on the diagonal of square is the double of the area of the square region.
Ans: 
7>Prove that any square region is one half of the square region drawn on its diagonal.
Ans:
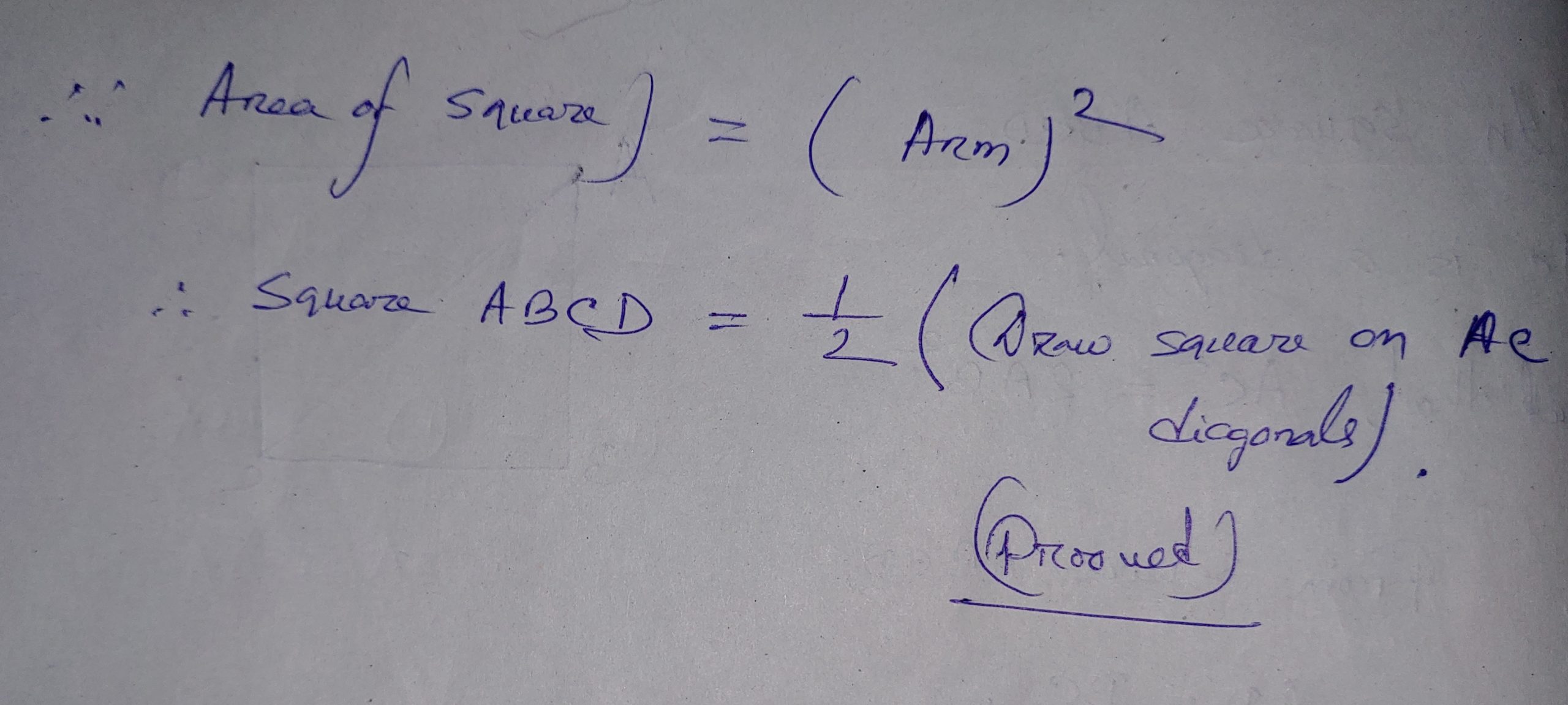
8> In triangle ABC, A= 1 right angle and D is a point on AC. Prove that BC2 + AD2 = BD² + AC2.
Ans:
9> In triangle ABC, ∠A= 1 right angle. If D and E are respectively the mid points of AB and AC, prove that DE = CE + BD².
Ans:
10> In ꕔ ABC, AD is the perpendicular to BC and AB>AC. Prove that AB2 – AC2 = BD2 – CD².
Ans: 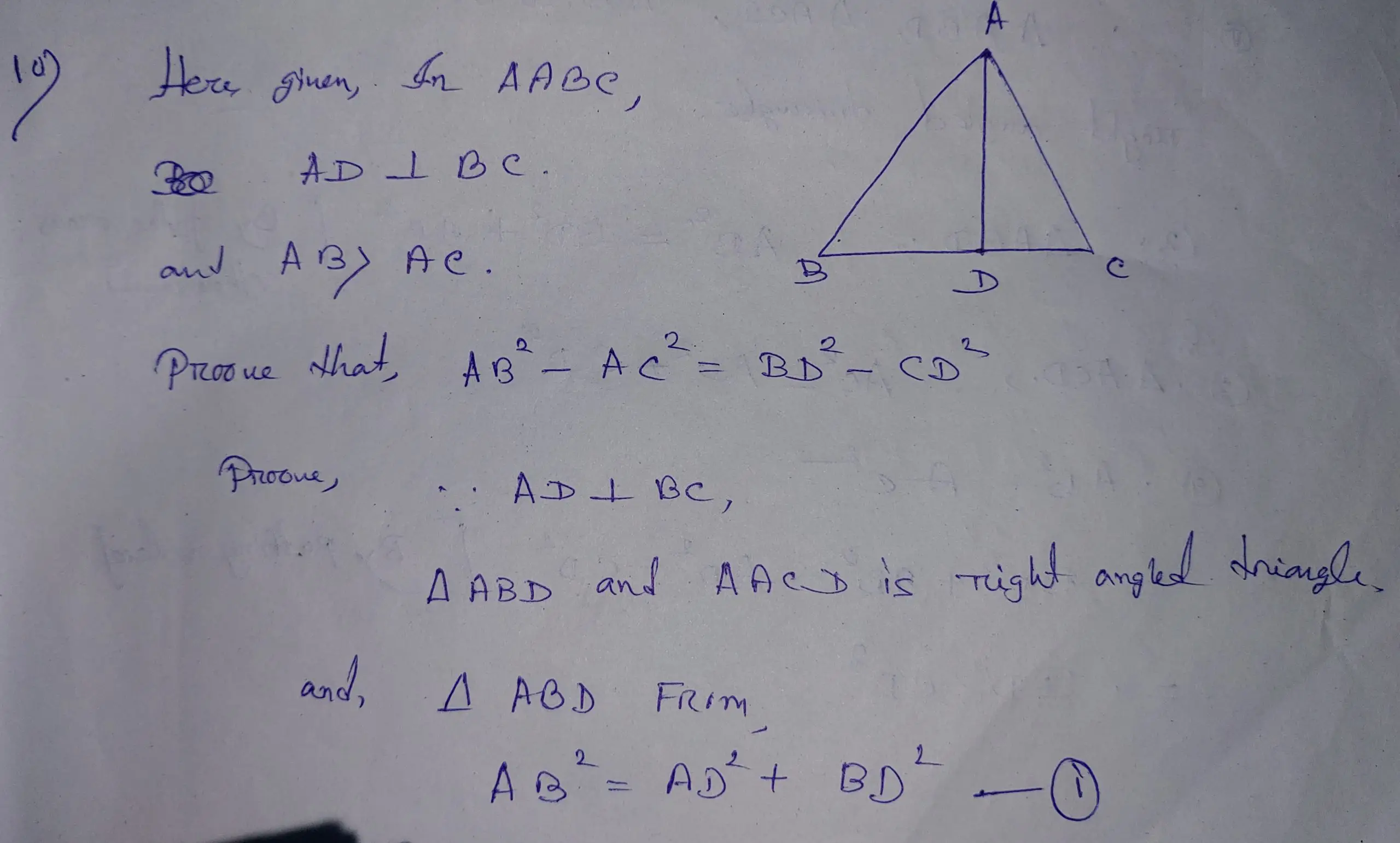

11> In ꕔ ABC, AD is the perpendicular to BC and P is any point on AD and AB>AC. Prove that PB2 – PC2 = AB² – AC².
Ans:
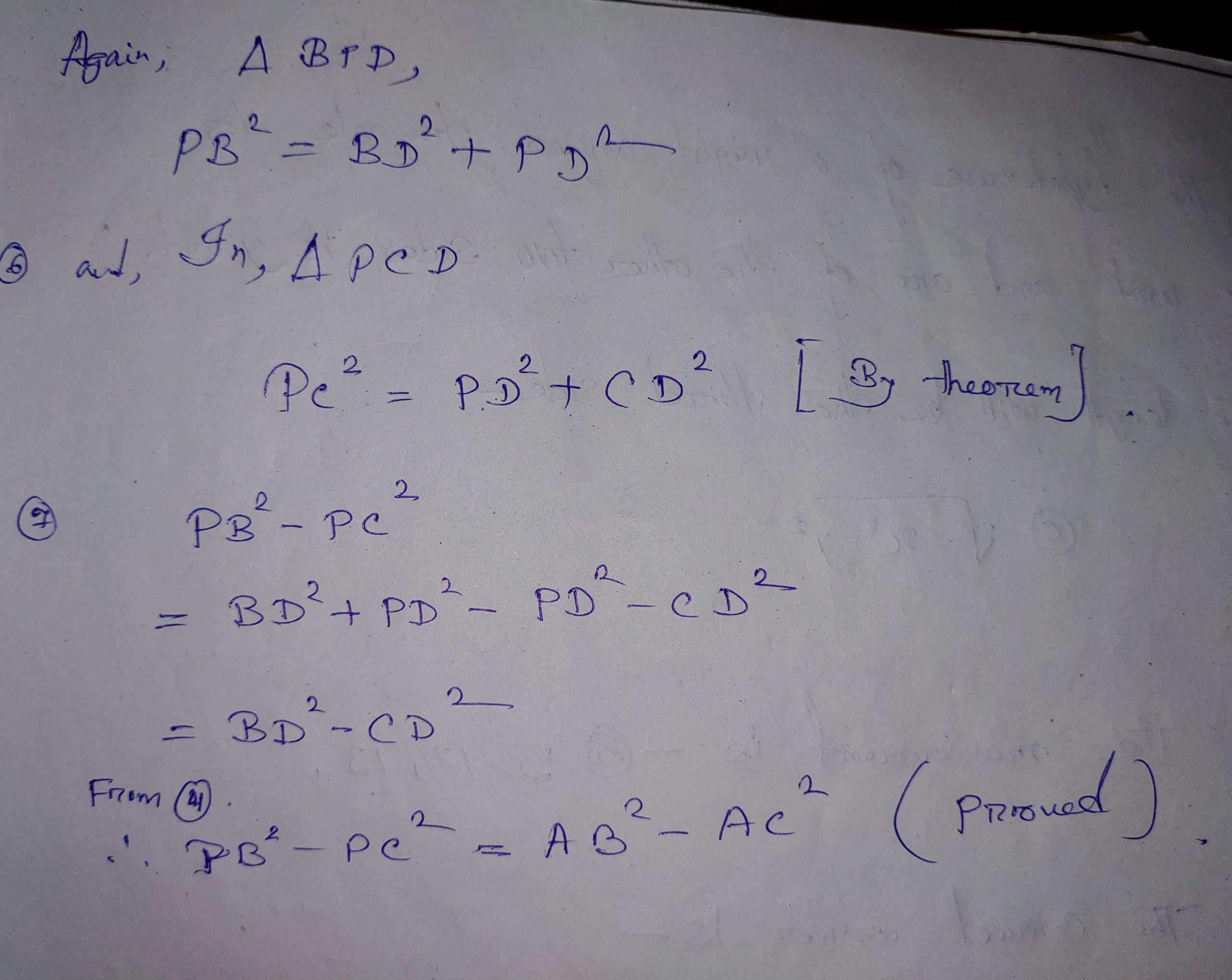
12> The ratio of the three sides of a triangle is 1:1:√2. What is the value of the greatest angle?
Ans: 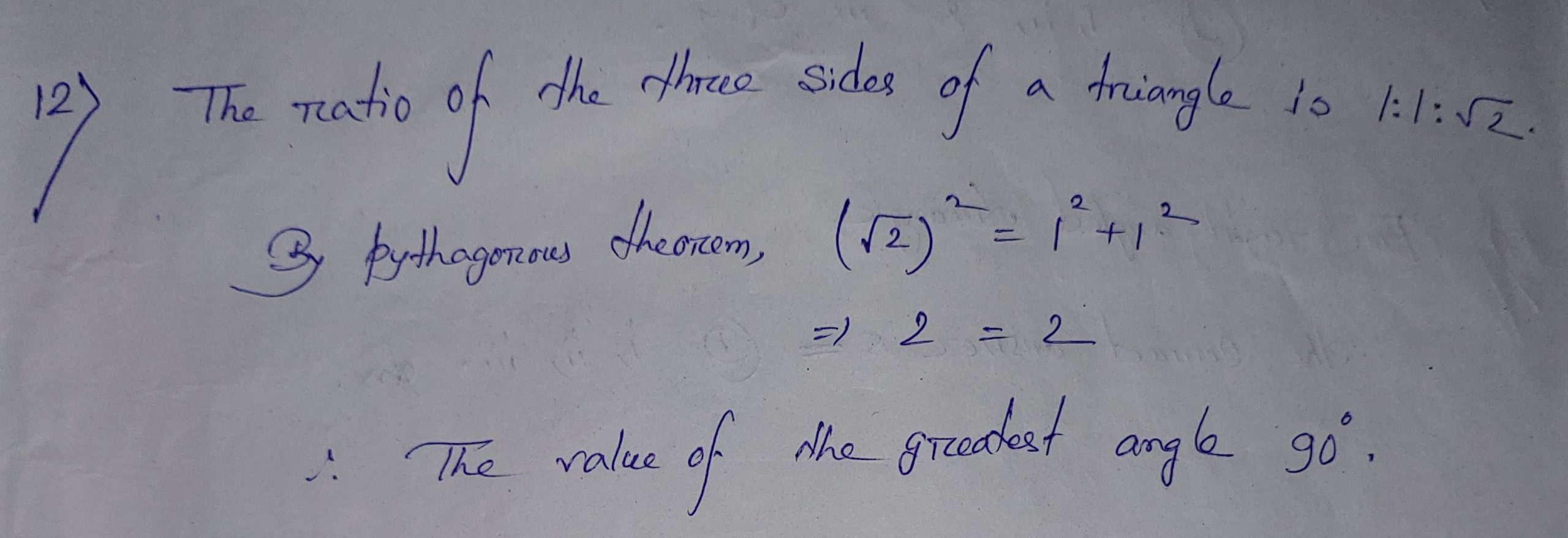
13> For a right angled triangle, the difference between two acute angles is 5°. What is the value of the smallest one?
Ans: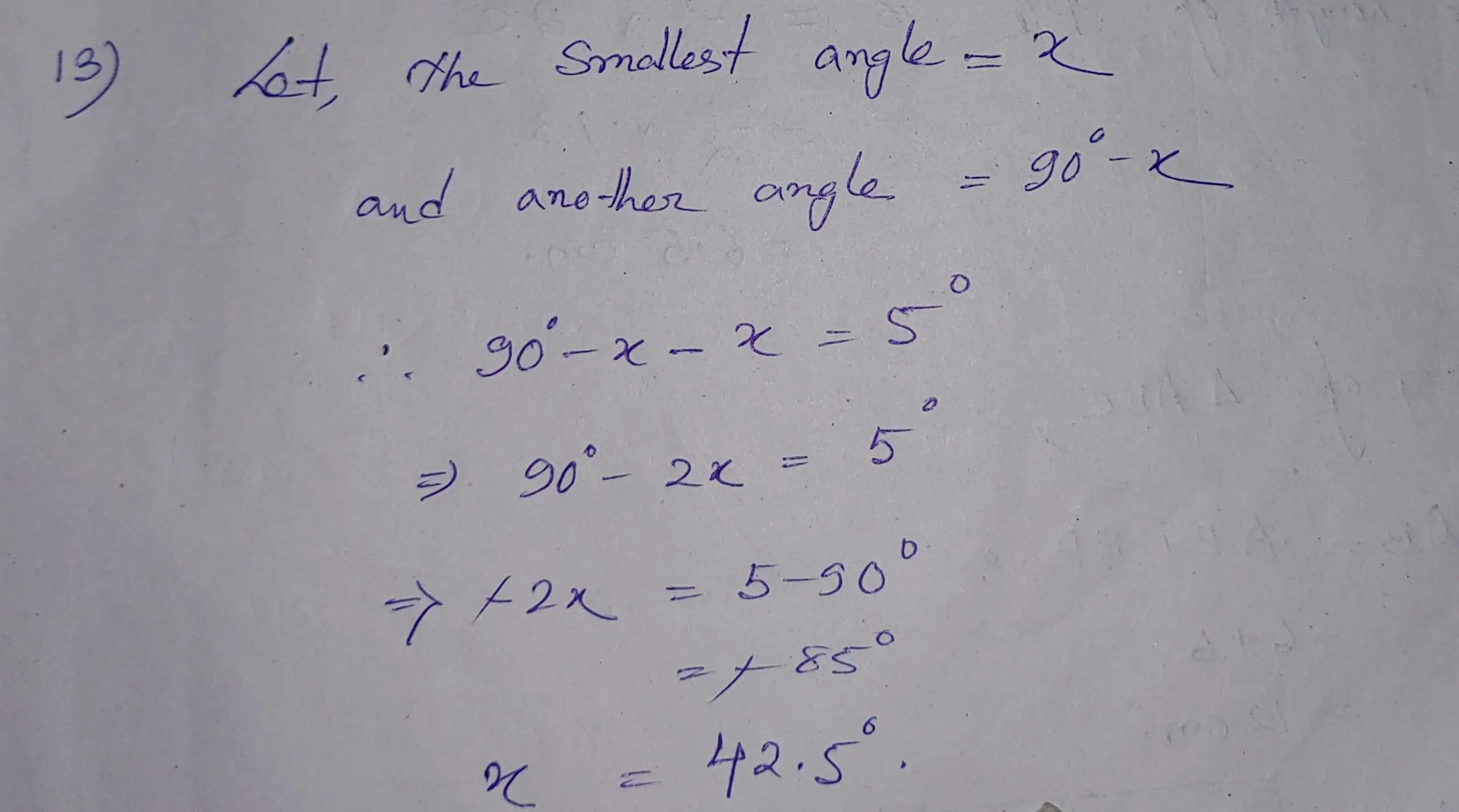
14> The hypotenuse of a right angled triangle is x unit and one of the other two sides is y unit. What will be the length of the third side?
Ans: The hypotenuse of a right angled triangle is X unit and one of the other two sides is y unit. The length will be the third side –
(c) √x2-y2
15> For which of the following measurements, is it possible to draw a right angled triangle?
Ans: The measurement is – (b) 5,12,13
16> In ꕔ ABC, ∠A = 1 right angle
Ans: (d)
17> For a right angled triangle-
i> the longest side in hypotenuse.
ii> sum of the square of the smaller sides is equal to the square of the longest side.
iii> Acute angles are complementary to each other. Which one of the following is correct?
Ans: (d)
18> What will be the value of PQ in cm ?
Ans: The length os PQ is = ½ x BC
= ½ x 13
= 6.5 cm.
19> What will be the area of ꕔ ABC in sq.cm ?
Ans: The area of ꕔ ABC ,
AB = AP+BP
= 6+6
= 12CM.
Therefore, AC = √BC2-AB2
= √132-√122.
= √189-√144
= 5 CM.
Therefore, ꕔ ABC = ½ x AB x AC
= ½ x 12 x 5
= 30cm2
20> What will be the perimeter of ꕔ APQ in cm ?
Ans: Perimeter of ꕔ APQ = AP + AQ + PQ
= (6 + 2.5 + 6.5)
= 15 CM
21> In the polygon ABCDE, AE || BC, CF T AE and DQ T CF. ED= 10 mm, EF=2 mm. BC= 8 mm, AB=12 mm. On the basis of the above information, answer the questions (1-4):
(1) What is the area of the quadrilateral ABCF in square millimetres?
(2) Which one of the following indicates the area of the triangle FPC in sq. m.?
(3) Which one of the following expresses the length of CD in millimetre?
(4) Which one of the following indicates the difference between the areas of ꕔ FPC and ꕔ DQC?
Ans: (1) & (2) 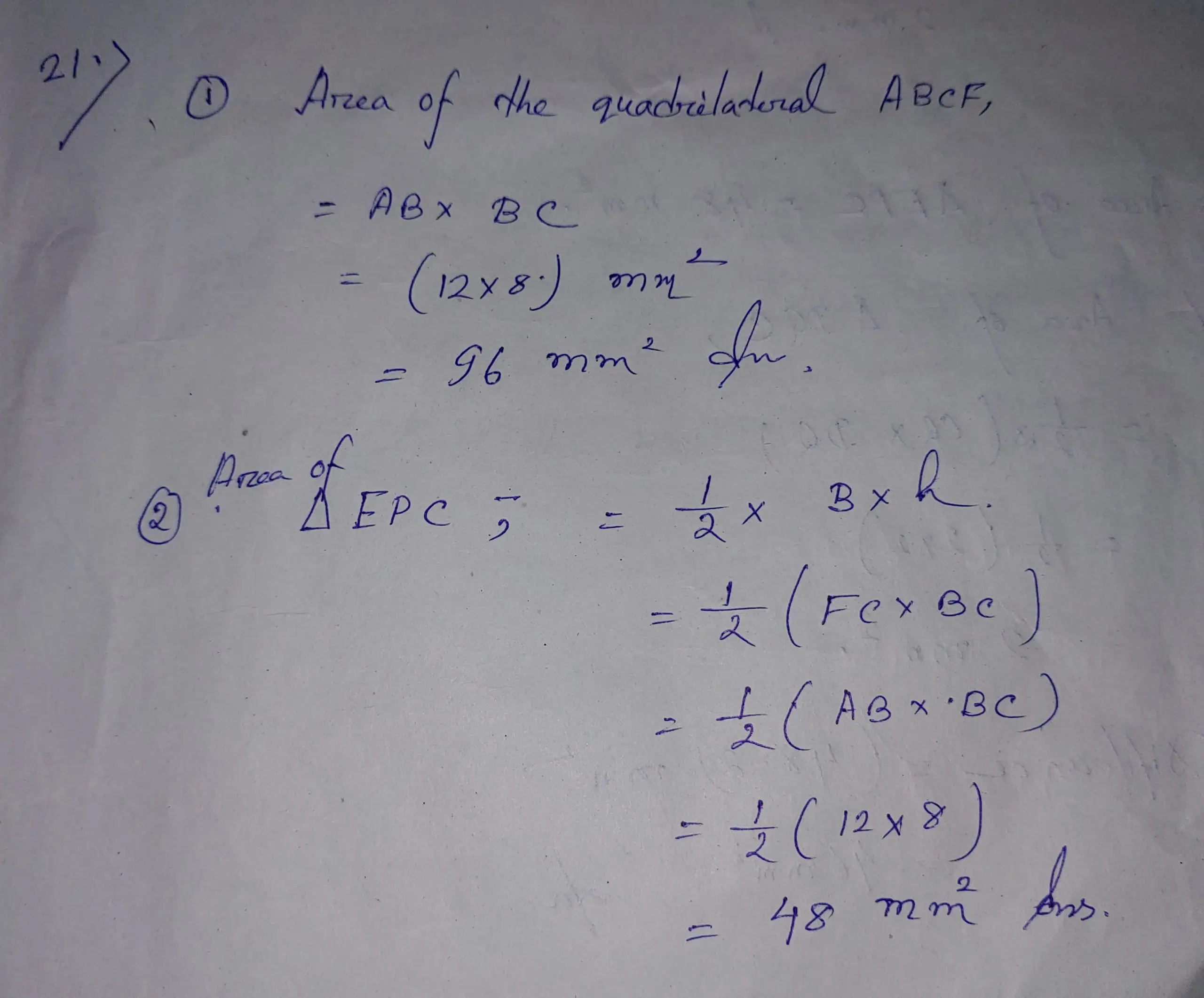
(3) 
