NCTB Class 8 Math Chapter Ten Exercise 10.1 Solutions by Math Expert. Bangladesh Board Class 8 Math Solution Chapter Ten Circle Exercise 10.1 Solution.
|
Board |
NCTB |
| Class |
8 |
|
Subject |
Mathematics |
| Chapter |
10 |
|
Chapter Name |
Circle |
| Exercise |
10.1 Solution |
Exercise 10.1
1> Prove that, if two chords of a circle bisect each other, their point of intersection will be the center of the circle.
Ans:
2> Prove that the line joining the midpoints of two parallel chords passes through the centre and is perpendicular to the two chords.
Ans:

3> Two chords AB and AC of a circle make equal angles with the radius through A. Prove that AB=AC.
Ans:

4> In the figure, O is the centre of the circle and the chord AB chord AC. Prove that ∠BAO = ∠CAO.
Ans:
6> A chord AB of one of two concentric circles intersect the other at C and D. Prove that AC=BD.
Ans: Let, O is the centre of circle AFB & CHD
AB is the chord of the circle AFB, touches the circle CHD at point C &D
Prove that, AC = BD
Draw: OE Ʇ AB
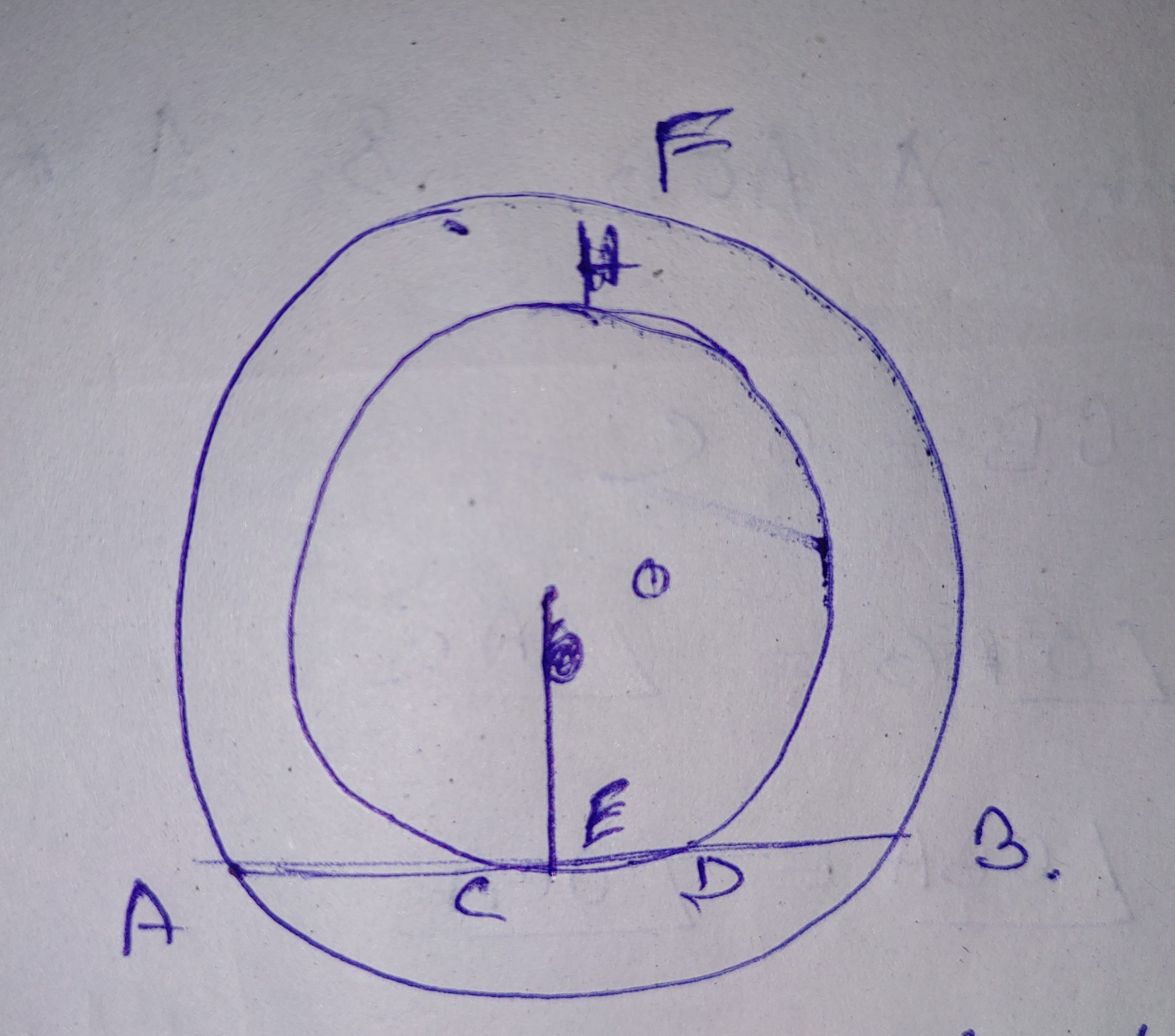
Proof: O is the centre of circle AFB
OE Ʇ AB
AE = BE , and, OE Ʇ CD [ From circle CHD]
Therefore, CE = DE
Now, AE – CE = BE – DE
AC = BD
Therefore, AC = BD (proved)