Collins Maths Solutions Class 6 Chapter 6 Playing with Numbers
Welcome to NCTB Solution. Here with this post we are going to help 6th class students for the Solutions of Collins Maths Class 6 Mathematics, Chapter 6, Playing with Numbers. Here students can easily find Exercise wise solution for chapter 6, Playing with Numbers. Students will find proper solutions for Exercise 6.1, 6.2, 6.3, 6.4, 6.5, 6.6, 6.7 and 6.8 Our teacher’s solved every problem with easily understandable methods so that every students can understand easily. Here in this post all the solutions are based on ICSE latest Syllabus.
Playing with Numbers Exercise 6.1 Solution :
Question no – (1)
Solution :
(a) {24 – (-3)} ÷ (- 9) × 6
= {24 + 3} ÷ (- 9) × 6
= 27 ÷ (- 9) × 6
= (- 3) × 6
= – 18…(Simplified by BODMAS rule)
(b) 12 – 36 ÷ (- 9)
= 12 – (4)
= 12 + 4
= 16…(Simplified by BODMAS rule)
(c) 7 – 3 × (- 5)
= 7 – (- 15)
= 7 + 15
= 22…(Simplified by BODMAS rule)
(d) (-18) ÷ {6 – (-3)} + 4
= (-18) ÷ {6 + 3} + 4
= (-18) ÷ 9 + 4
= – 2 + 4
= 2…(Simplified by BODMAS rule)
(e) (- 9) + 27 ÷ (- 9)
= (- 9) + (- 3)
= – 9 – 3
= – 12…(Simplified by BODMAS rule)
(f) (-5) × (-11) – 5 × 6
= + 55 – 30
= + 25…(Simplified by BODMAS rule)
(g) {9 × (- 7)} ÷ 3 + 21
= (- 63) ÷ 3 + 21
= – 21 + 21
= 0…(Simplified by BODMAS rule)
(h) {9 – (18)} ÷ 9 – (- 2)
= {9 + 18} ÷ 9 – (- 2)
= 27 ÷ 9 – (- 2)
= 3 (- 2)
= 3 + 2
= 5 (Simplified by BODMAS rule)
Question no – (2)
Solution :
(a) 25 + 50 × 20 – (- 14) + (33 ÷ 3)
Now, 25 + 50 × 20 – (- 14) + (33 ÷ 3)
= 25 + 50 × 20 – (- 14) + 11
= 25 + 1000 + 14 + 11
= +1050
(b) {(90 + 50) – 22} + 4 × 25 – 20
Now, {(90 + 50) – 22} + 4 × 25 – 20
= {140 – 22} + 100 – 20
= 118 + 100 – 20
= 218 – 20
= 198
(c) 30 – [18 – {14 – (15 – 4 ÷ 2 × 2)}]
Now, 30 – [18 – {14 – (15 – 4 ÷ 2 × 2)}]
= 30 – [18 – {14 – 915 – 2 × 2)}]
= 30 – [18 – {14 – (15 – 4)}]
= 30 – [18 – {14 – 11{]
= 30 – [18 – 3]
= 30 – 15
= 15
(d) [50 – (- 2) {6 – (7 – 3)}] ÷ [3 × {5 + 13}]
Now, [50 – (- 2) {6 – (7 – 3)}] ÷ [3 × {5 + 13}]
= [50 – (2){ 6 – 4}] ÷ [3 × 18]
= [50 – (- 2) (2)] ÷ [3 × 18]
= [50 – (- 4)] ÷ 54
= [50 + 4] ÷ 54
= 54 ÷ 54
= 1
Playing with Numbers Exercise 6.2 Solution :
Question no – (1)
Solution :
(a) 6 is a factor of 42 – this statement is Correct.
(b) 24 is not a multiple of 5 – this statement is Incorrect.
(c) 20 is a multiple of 3 – this statement is Incorrect.
(d) 3 and 15 are factors of 54 – this statement is Incorrect.
Question no – (2)
Solution :
(a) All the possible Factors of 40 are 1, 2, 4, 5, 8, 10, 40.
(b) All the possible Factors of 65 are 1, 5, 13, 65.
(c) All the possible Factors of 90 are 1, 2, 3, 5, 9, 10, 18, 6, 30, 45, 90.
(d) All the possible Factors of 150 are 1, 2, 3, 5, 9, 10, 18, 6, 30, 45, 90.
Question no – (3)
Solution :
(a) First 6 Multiples of 3 are 3, 6, 12, 15, 18, 21
(b) First 6 Multiples of 11 are 11, 22, 33, 44, 55, 66
(c) First 6 Multiples of 8 are 8, 16, 24, 32, 40, 48
(d) First 6 Multiples of 4 are 4, 8, 12, 16, 20, 24
Question no – (4)
Solution :
(a) The smallest factor of 55 other than 1 is 5
(b) The largest factor of 10 is 10
(c) The 5th multiple of 9 is 45
Playing with Numbers Exercise 6.3 Solution :
Question no – (1)
Solution :
(a) Prime numbers :
A number which has only two factors that is 1 and the number itself.
Examples of prime numbers are 2, 3, 5, 7, 11
(b) Co-prime numbers :
Two numbers are said to be co-prime or relatively prime if their common factor is only 1
Examples of Co-prime numbers 2 and 5
(c) Composite numbers :
A number which has more than two factor that is composite number.
Examples of Composite number 4, 6, 9, 10
(d) Twin prime numbers :
If the difference between two prime numbers is 2 then they are said to be twin prime.
Examples of Twin prime number 3 and 5 and 11 and 13
Question no – (2)
Solution :
(a) 17
∴ It is not a composite number because if has only two factor that is 1 and 17.
(b) 15
= 15 is a composite number
It has more than two factor that is 1, 3, 5, 15
(c) 23
= 23 is not a composite number
(d) 91
= 91 is a composite number
It has more than two factors that is 1, 7, 13, 91
Question no – (3)
Solution :
(a) Prime numbers between 3 and 21 are 5, 7, 11, 13, 17, 19
(b) Prime numbers between 15 and 50 are 17, 19, 23, 29, 31, 41, 43, 47
(c) Prime numbers between 64 and 87 are 67, 71, 73, 79
(d) Prime numbers between 64 and 87 are 67, 71, 73, 79
Question no – (4)
Solution :
(a) All odd numbers are prime numbers → False
Reason : All odd numbers are not prime number such as a is a odd number but is not a prime number and 2 is even number though it is prime number.
(b) All even numbers are composite numbers → False
Reason : All even number is not a composite number because 2 is an even number and it is prime number also.
(c) Two consecutive odd prime numbers are twin primes → True
Reason : Such as 3 and 5 are two consecutive odd prime numbers and they are twin prime.
(d) 2 is the only even prime number → True.
Reason : Yes, 2 is the only even prime number and without 2 all prime numbers are odd.
(e) All co-primes are prime numbers but all prime numbers need not be co-primes → False
Reason : CO-prime numbers may not be prime numbers.
Question no – (5)
Solution :
From 1 to 100 total 74 numbers are composite number.
And, 63, 33, 93 are composite number with digit 3 in one’s places.
Question no – (6)
Solution :
Seven consecutive composite number are 91, 92, 93, 94, 95, 96, 97
Playing with Numbers Exercise 6.4 Solution :
Question no – (1)
Solution :
| Number | Divisible by |
|||||||||
| 7020 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 11,456 | Yes | A 0 + 2 = 9 Yes |
Yes | Yes | Yes | No | No | Yes | Yes | No |
| 7,31,541 | Yes | No | Yes | No | No | No | Yes | No | No | No |
| 97,240 | No | No | No | No | No | No | No | No | No | No |
| 7,89,430 | Yes | No | Yes | Yes | No | No | No | No | Yes | Yes |
| Yes | No | Yes | No | No | No | No | Yes | No |
Question no – (2)
Solution :
(a) All numbers that are divisible by 9 are not necessarily divisible by 3 → False.
(b) If two given numbers are divisible by a number, then their difference/sum is also divisible by that number → True.
(c) If a number is divisible by 2 and 5, then it is also divisible by the sum of 2 and 5, that is, 7 → False.
(d) 84 is divisible by 4 and also by the multiples of 4 → False.
Playing with Numbers Exercise 6.5 Solution :
Question no – (1)
Solution :
Given, 136
∴ 136 = 2 × 2 × 2 × 17 × 1
Question no – (2)
Solution :
Given, 252
∴ 252 = 2 × 2 × 3 × 3 × 7
Question no – (3)
Solution :
Given, 9317
∴ 9317 = 7 × 11 × 11 × 11
Question no – (4)
Solution :
Given, 1035
∴ 1035 = 3 × 3 × 5 × 23
Question no – (5)
Solution :
Given, 13,915
∴ 13,915 = 5 × 11 × 11 × 23
Playing with Numbers Exercise 6.6 Solution :
(1) Find the HCF of each pair of numbers by listing the factors
Solution :
(a) Given in the question, 12 and 28
The factors of 32 are, 1, 2, 3, 4, 6, 12
The factors of 28 are 1, 2, 4, 7, 14, 28
The common factors are 2, 4
Therefore, the H.C.F of 12 and 28 is 4
(b) In the question, 30 and 12
The factors of 30 are = 1, 2, 3, 5, 10, 15, 30,
The factors of 12 are = 1, 2, 3, 4, 6, 12
∴ The common factors are, 2, 3, and 6
Hence, the H.C.F of 30 and 12 are 6
(c) In the question we get, 24 and 48
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
∴ The common factors are 2, 3, 4, 6, 8, 12, 24
Thus, the HCF of 24 and 48 is 24
(d) 45 and 72
The factors of 72 are 1, 3, 5, 9, 15, 45
The factor of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
∴ The common factors are 3, 9
Therefore, the HCF of 45 and 72 is 9
Question no – (2)
Solution :
(a) 12 and 28

Prime factors of 13 = 13 × 1
Prime factors of 65 = 13 × 5
Therefore, the HCF of 13 and 65 is 13.
(b) 64 and 120

= Prime factors of 64 = 2 × 2 × 2 × 2 × 2 × 2 × 1
= Prime factors of 120 = 2 × 2 × 2 × 3 × 5 × 1
Therefore the HCF of 64 and 120 is 2 × 2 × 2 = 8
(c) 36 and 12

= Prime factors of 36 = 2 × 2 × 3 × 3 × 1
= Prime factors of 12 = 2 × 2 × 3 × 1
Therefore the HCF of 36 and 12 s i2 × 2 × 3 = 12
(d) 40 and 85

= Prime factors of 40 is = 2 × 2 × 2 × 5 × 1
= prime factors of 88 is = 2 × 2 × 2 × 11 × 1
Therefore, H.C.F of 40 and 88 is 2 × 2 × 2 = 8
Question no – (3)
Solution :
(a) 13 and 65
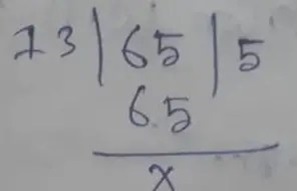
Therefore H.C.F of 13, 65 is 13
(b) 120 and 280

Therefore, HCF of 120, 280 is 40
(d) 658 and 770

Therefore, HCF of 658 and 770 is 14
Question no – (4)
Solution :
The largest size of grass patch the that can be used to cover the lawn will be the HCF of dimensions of lawn.
So,
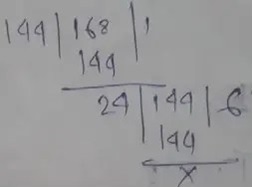
So, the HCF of 144 and 168 is 24
Therefore, 24 m is the largest size of grass patch that can be used to cover the lawn.
Question no – (5)
Solution :
The HCF of 480 and 672

∴ The HCF of 480 and 672 is 96
Therefore, the maximum numbers of students are 96 in each group such that no students is left out.
Playing with Numbers Exercise 6.7 Solution :
Question no – (1)
Solution :
(a) 2 and 3
Now by the common multiple method,
The multiple of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18
The multiples of 3 are 3, 6, 9, 12, 15, 18, 21
So, the common multiples of 2 and 3 are 6 and 12
Therefore, the LCM of 2 and 3 and 3 are 6.
(b) 4 and 7
Now, by Common Multiple Method
The multiples of 4 are 4,8, 12, 16, 20, 24, 28, 36
The multiples of 7 are 7, 14, 28, 25, 42
Hence, The common multiples of 4 and 7 are 28
(c) 5 and 15
Now, by Common Multiple Method,
The multiples of 5 are 5, 10, 15, 20, 25, 30, 35
The multiples of 15 are 15, 30, 45, 60
∴ The common multiples of 5 and 15 is 15, 30
Therefore LCM of 5 and, 15 is 15
(d) 10 and 25
Now, by Common Multiple Method,
The multiples of 10,20,30,40 50,60,70, 80,90,100,
The multiples of 25 are 25, 50, 75, 100
So, the common multiples off 10 and 25 are 50, 100
Therefore, LCM of 10 and 25 is 50
Question no – (2)
Solution :
(a) LCM of 24 and 36 using Prime Factorisation Method,

= 24 = 2 × 2 × 2 × 3
= 36 = 2 × 2 × 3 × 3
∴ LCM of 24 and 36 is,
= 2 × 2 × 3 × 3
= 36 × 2
= 72
Thus, the LCM of 24 and 36 is 72
(b) LCM of 24 and 80 using Prime Factorisation Method,

= 24 × 2 × 2 × 2 × 3
= 80 × 2 × 2 × 2 × 2 × 5
∴ LCM of 24 and 80 is,
= 2 × 2 × 2 × 2 × 3 × 5
= 240
Hence, the LCM of 24 and 80 is 240
(c) LCM of 90 and 125 using Prime Factorisation Method,

= 90 = 2 ×3 × 3 × 5
= 125 = 5 × 5 × 5
∴ LCM of 90 and 125 is,
= 2 × 3 × 3 × 5 × 5 × 5
= 2205
Therefore, the LCM of 90 and 125 is 2205.
(d) LCM of 160 and 112 using Prime Factorisation Method,

= 160 = 2 × 2 × 2 × 2 × 2 × 5
= 112 = 2 × 2 × 2 × 2 × 7
∴ LCM of 160 and 112 is,
= 2 × 2 × 2 × 2 × 2 × 7
= 1120
Hence, the LCM of 160 and 112 is 1120.
Question no – (4)
Solution :
As per the question, 20 and 45
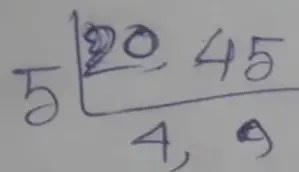
∴ LCM of 20 and 45
= 5 × 4 × 9
= 180
Therefore, after 180 days they will meet again at the same market.
Question no – (5)
Solution :

∴ L.C.M of 28 and 36,
= 2 × 2 × 7 × 9
= 252
∴ The number leaves 9 as the remainder,
= 252 + 9
= 261
Therefore, the required number will be 261.
Playing with Numbers Exercise 6.7 Solution :
Question no – (1)
Solution :
As we know that,
Product of two numbers = their HCF × their LCM
Now,
∴ 4 × 5 = 20 × HCF
= HCF = 4 × 5/20
= HCF = 1
Therefore, their HCF is 1
Question no – (2)
Solution :
As we know,
12 × 16 = 4 × LCM
∴ LCM = 12 × 164/4
= 48
Therefore, the LCM of 12 and 16 will be 48
Question no – (3)
Solution :
According to the rule,
12 × 14 = 84 × HCF
∴ LCM of 12 and 14
= 12 × 14/84
= 2
Therefore, the HCF of 12 and 14 will be 2
Question no – (4)
Solution :
According to the rule,
12 × other number = HCF × LCM
∴ Other number,
= 6 × 36/12
= 18
Therefore, the other number will be 18
Question no – (5)
Solution :
According to the rule,
HCF × LCM = 120 × other number
= 24 × 240 = 120 × other number
∴ Other number,
= 24 × 240/120
= 48
Therefore, the other number will be 48
Next Chapter Solution :
👉 Chapter 7 👈