Samacheer Kalvi Class 9 Maths Chapter 6 Trigonometry Solutions
Welcome to NCTB Solutions. Here with this post we are going to help 9th class students by providing Solutions for Samacheer Kalvi Class 9 Maths chapter 6 Trigonometry. Here students can easily find all the solutions for Trigonometry Exercise 6.1, 6.2, 6.3, 6.4 and 6.5. Also here our Expert Maths Teacher’s solved all the problems with easily understandable methods with proper guidance so that all the students can understand easily. Here in this post students will get chapter 6 solutions. Here all the solutions are based on Tamil Nadu State Board latest syllabus.

Trigonometry Exercise 6.1 Solutions :
(1) From the given figure, find all the trigonometric ratios of angle B.

Solution :
Sin B = 9/41
Cos B = 40/41
Tan B = 9/40
Cosec B = 41/9
Sec B = 41/40
Cot B = 40/9
(2) From the given figure, find the values of
(i) sin B
(ii) sec B
(iii) cot B
(iv) cos C
(v) tan C
(vi) cosec C
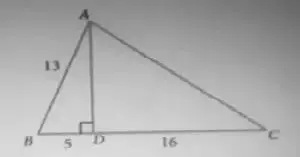
Solution :
(i) Sin B = 12/13
(ii) Sec B = 1/Cos B
= (1/15)/13
= 13/5
(iii) Cot B = 12/5
(iv) Cos C = 16/20
(v) Tan C = 12/16
(vi) Cosec C = 20/12
(3) If 2 cos θ = √3, then find all the trigonometric ratios of angle θ
Solution :
2 Cos = √3
Cos θ = √3/2
x = √2² ± √(3)²
= √4-3
= 1
So, Sin θ = 1/2
Cosec θ = √3/2
Tan θ = 1√3
Cosec θ = 2
sec θ = 2√3
cot θ = √3
(4) If cos A = 3/5, then find the value of sin A – cos A/2 tan A
Solution :
Sin A = 4/5
tan A = 4/5
sin A – cos A/2 tan A
= (4/5 – 3/5) / 2 × 4/3
= 1/5 × 3/8
= 3/40
(5) If cos A = 2x/1 + x², then find the values of sin A and tan A in terms of x
Solution :
Cos A = 2x/1 + x²
So, (1 + x²)² = (2x)² + x²
= x² = 1 + x⁴ + 2x² – 4x²
= 1 + x⁴ – 2x²
= x² = (1 – x²)²
∴ x =1 – x²
∴ Sin A = 1 – x²/1 + x²
∴ tan A = 1 – x²/2x
(6) If sin θ = a/√a² + b² then show that b sin θ = a cos θ
Solution :
sin θ = a/√a² + b² Cos Q= b/√a² + b² [Obviously]
bin θ = bx = a/√a² + b² = ab/√a² + b²
Cos θ = ax b/√a² + b² = a3/√a² + b²
Therefore, b sin θ = a Cos θ
(7) If 3 cot A = 2, then find the value of 4 sinA – 3 cosA/2 sinA + 3 cosA
Solution :
3 Cot A= 2
= cos A = 2/3
tan A =3/2
= 4 sinA – 3 cosA/2 sin A + 3 cos A
= (4×3/√13-3×2/√13) /(2×3/√13+3×2/√13)
= (12/√13 -6/√13) / (6/√13 +6/√13)
= (6/√13 x / √13 /12)
= 1/42
(8) If cosθ : sinθ = 1 : 2, then find the value of 8 cosθ – 2 sinθ/4 cosθ+2 sinθ
Solution :
cosθ : sin = 1:2
= cosθ/sinθ = 1/2
= sin θ = 2 cos θ .
∴ 8 cos θ-2sin θ/4cos θ+2sin θ
= 8 × 1/2 sin θ / 2 sin θ/4 × 1/2 sin θ + 2 sin θ
= 8×1/2si θ-2sin θ/2sin θ+2sin θ
= b2sin θ/4sin θ
= 1
Trigonometry Exercise 6.2 Solutions :
(1) Verify the following equalities :
(i) sin²60°+cos²60 = 1
(ii) 1+tan²30° = Sec²30°
(iii) cos90° = 1 – 2sin² 45°= 2cos² 45° – 1
(iv) sin30° cos60° + cos30° sin60° = sin 90°
Solution :
(i) sin²60°+cos²60 = 1
= sin²60° + cos²60
= (√3/2)² + (1/2)²
= 3/4+1/4
= 4/4 = 1 (Proved)
(ii) 1+tan²30° = Sec²30°
= 1+tan²30° RHS Sec²30°
= 1+(√3) = (2√3) ²
= 1+1/3 = 3/4
= 3/4
(iii) cos90° = 1 – 2sin² 45°= 2cos² 45° – 1
= 1cos 90°= 0
And = 1-2sin² 45°
= 1-2×(1/√2) ²
= 1-2×1/2 = 0
(iv) sin30° cos60° + cos30° sin60° = sin 90°
LHS sin 30°cos 60° = Cos 30°sin 60°
= 1/2×1/2 +√3/2 × √3/2
= 1/4+1/4
= 4/4 = 1
RHS Sin 90° = 1
Therefore, LHS = RHS.
(2) Find the value of the following :
(i) tan45°/cosec30° + sec60°/cot45° – 5sin90°/2cos0°
(ii) (sin90° + cos60° + cos45°) × (sin30° + cos0° – cos45°)
(iii) Sin²30° – 2cos³60° + 3tan⁴45°
Solution :
(i) tan45°/cosec30° + sec60°/cot45° – 5sin90°/2cos0°
= 1/2 + 2/1 – 5 × 1/2 × 1
= 1 + 4-5/2
= 0
(ii) (sin90° + cos60° + cos45°) × (sin30° + cos0° – cos45°)
= (1 + 1/2 + 1/√2) × (1/2 + 1 – 1/√2)
= {(1 + 1/2) – 1/√2)} {(1 + 1/2) – 1/√2}
= (1+ 1/2)² – (1/√2)²
= 1 + 1 + 1/4 – 1/2
= 8 + 1 – 2/4
= 7/4
(iii) Sin²30° – 2cos³60° + 3tan⁴45°
= (1/2)² – 2 (1/2)³ + 3 (1)⁴
= 1/4 – 2 × 1/8 + 3
= 1-1 + 12/4
= 3
(3) Verify cos3A = 4cos³ A – 3cosA, when A = 30°
Solution :
L.H.S, Cos3A
= Cos (3×30°)
= Cos90° = 0
R.H.S, 4cos³A – 3cosA
= 4cos³30° – 3cos30°
= 4 × (√3/2)³ – 3 × √3/2
= 4 × 3√3/8 – 3√3/2
= 0
Therefore, LHS = RHS.
(4) Find the value of 8 sin2x cos4x sin6x, when x = 15°
Solution :
Given, 8sin2x cos4x sin6x
= 8sin30° cos60° sin90°
= 8 × 1/2 × 1/2 × 1
= 2
Therefore, the value will be 2
Trigonometry Exercise 6.3 Solutions :
Find the value of the following :
(i) (Cos47°/Sin43°)² + (Sin72°/Cos18°)² – 2cos² 45°
Solution :
(Cos47°/Sin43°)² + (Sin72°/Cos18°)² – 2cos² 45°
= (cos (90°-43°)/Sin43°)² + (Sin (90° – 18°)/Cos18)² – 2cos² 45°
= 1² + 1² – 2 (1/√2)²
= 1 – 2 × 1/2
= 1
So, the value is = 1
(ii) Cos70°/Sin20° + Cos59°/Sin31° + Cosθ/sin (90° – θ) – 8cos² 60°
Solution :
Cos70°/Sin20° + Cos59°/Sin31° + Cosθ/sin (90° – θ) – 8cos² 60°
= Sin20°/Sin20 + Sin31/sin31 + cosθ/cosθ – 8cos² 60°
= 1+1+1 – 8 × (1/2)²
= 3 – 2
= 1
Hence, the value is = 1
(iii) tan15° tan30° tan45° tan60° tan75°
Solution :
tan15° tan30° tan45° tan60° tan75°
= tan (9°75) tan (90° – 60°) tan45° tan60° tan75°
= cot75° cot60° × 1 × tan60° tan75
= 1/tan75° × 1/tan60° × 1 × tan60° × tan75°
= 1
Thus, the value is 1
(iv) Cotθ/tan (90° – θ) + cos(90° – θ) tanθ sec (90° – θ)/sin (90° – θ) cot (90° – θ) cosec (90° – θ)
Solution :
Cotθ/tan (90° – θ) + cos(90° – θ) tanθ sec (90° – θ)/sin (90° – θ) cot (90° – θ) cosec (90° – θ)
= cotθ/cotθ + Sinθ.tanθ.cosecθ/cosecθ tanθ secθ
= 1 + sinθ/cosθ . 1/sinθ × cosθ/1
= 1 + 1
= 2
Therefore, the value is 2
Trigonometry Exercise 6.4 Solutions :
(2) Find the value of θ if
(i) Sinθ = 0.9975
(ii) Cosθ = 0.6763
(iii) tanθ = 0.0720
(iv) cosθ = 0.0410
(v) tanθ = 7.5958
Solution :
(i) Sinθ = 0.9975
= If θ = 85°. 57′
So, value of θ = 85°. 57′
(ii) Cosθ = 0.6763
If θ = 47°.27′
So, value of θ = 47°.27′
(iii) tanθ = 0.0720
If θ = 4.7′
Hence, Value of θ = 4.7′
(iv) Cosθ = 0.0410
If θ = 87°.30
So, Value of θ = 87°.30
(v) tanθ = 7.5958
If θ = 82°.30
Therefore, Value of θ = 82°.30
(3) Find the value of the following :
(i) sin65°39′ + cos24°57′ + tan10°10′
(ii) tan70°58′ + cos15°26′ – sin84°59′
Solution :
(i) sin65°39′ + cos24°57′ + tan10°10′
= 0.9111 + 0.9066 + 0.1793
= 1.9970
(ii) tan70°58′ + cos15°26′ – sin84°59′
= tan70°58′ + cos15°26′ – sin84°59′
= 2.898 + 0.9639 – 0.9962
= 0.2.8659
(4) Find the area of a right triangle whose hypotenuse is 10 cm and one of the acute angle is 24°24′
Solution :
Angle = 24°24′
Hypotenuse = 10
So, sin24°24′ = 0.4131
= x/10 = 0.4131
= x = 4:13
And cos24°24′ = 0.9107
= y/10 = 0.9107
= y = 9.107
Area = 1/2×4.131×9.10.7
= 18.81
Hence, the area of a right triangle is 18.81
(5) Find the angle made by a ladder of length 5 m with the ground, if one of its end is 4 m away from the wall and the other end is on the wall.
Solution :
Length = 5
Base = 4
Cosθ = 4/5
= cosθ = 0.8
= θ = 36°52′
So, the angle made by a ladder 36°52′
(6) In the given figure, HT shows the height of a tree standing vertically. From a point P, the angle of elevation of the top of the tree (that is ∠P ) measures 42° and the distance to the tree is 60 metres. Find the height of the tree.
Solution :
Base = 60 m
So, tan42° = h/60
= 0.9004 = h/60
= h = 54.024
Then the height of the tree 54 (approximately)
Trigonometry Exercise 6.5 Solutions :
(1) If sin30° = x and cos60° = y, then x² + y² is
(1) 1/2
(2) 0
(3) Sin90°
(4) Cos90°
Solution :
Correct option – (1)
If sin30° = x and cos60° = y, then x² + y² is 1/2
(2) If tanθ = cot37°, then the value of θ is
(1) 37°
(2) 53°
(3) 90°
(4) 1°
Solution :
Correct option – (2)
The value of θ is 53°
(3) The value of tan72° tan18° is
(1) 0
(2) 1
(3) 18°
(4) 72°
Solution :
Correct option – (2)
The value of tan72° tan18° is 1.
(5) If 2sin2θ = √3, then the value of θ is
(1) 90°
(2) 30°
(3) 45°
(4) 60°
Solution :
Correct option – (2)
The value of θ will be 30°
(4) The value of 2tan30°/1 – tan²30° is equal to
(1) Cos60°
(2) Sin60°
(3) tan60°
(4) Sin30°
Solution :
Correct option – (3)
The value of 2tan30°/1 – tan²30° is equal to tan60°.
(6) The value of 3sin 70° sec20° + 2sin49° sec51° is
(1) 2
(2) 3
(3) 5
(4) 6
Solution :
Correct option – (3)
The value of 3sin 70° sec20° + 2sin49° sec51° is 5.
(7) The value of 1 – tan²45°/1 + tan²45° is
(1) 2
(2) 1
(3) 0
(4) 1/2
Solution :
Correct option – (3)
The value of 1 – tan²45°/1 + tan²45° is 0.
(8) The value of cosec (70° + θ) – sec (20° – θ) + tan (65° + θ) + cot (25° – θ) is
(1) 0
(2) 1
(3) 2
(4) 3
Solution :
Correct option – (1)
(70° + θ) – Sec (20 – θ) + tan (65 + θ) + cot (25 – θ)
= 1/sin (70 + θ) – 1/cos (20 – θ) + Sin (65 + θ)/Cos (65 + θ) – Cos (25 – θ)/Sin (25 – θ)
= 1/Cos (20 – θ) – 1/Cos (20 – θ) + Cos (25 – θ)/Sin (25 – θ) – Cos (25 – θ)/Sin (25 – θ)
= 0
(9) The value of tan1° tan2° tan3°…tan89° is
(1) 0
(2) 1
(3) 2
(4) √3/2
Solution :
Correct option → (2)
The value of tan1° tan2° tan3°…tan89° is 1.
Next Chapter Solution :